Неинерциальные системы отсчета, силы инерции

До сих пор движение тела рассматривалось по отношению к какой-либо одной из бесчисленного множества инерциальных систем отсчета. В такой системе отсчета основным уравнением движения тела является уравнение, выражающее второй закон Ньютона:

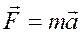(6.11)

Законы Ньютона выполняются только в инерциальных системах отсчета. Относительно всех инерциальных систем данное тело движется с одинаковым ускорением 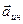. Поставим теперь задачу найти уравнение движения в неинерциальных системах отсчета, т.е. таких системах, в которых первый закон Ньютона не выполняется.

Любая неинерциальная система отсчета движется относительно инерциальных систем с некоторым ускорением, поэтому ускорение тела в неинерциальной системе отсчета 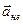будет отлично от .

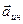Обозначим разность ускорения тела в инерциальной и неинерциальной системах символом :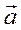

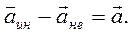(6.12)

В частном случае, когда неинерциальная система отсчета движется относительно инерциальной поступательно, ускорение тела 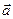одинаково для всех точек пространства 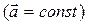и представляет собой ускорение неинерциальной системы отсчета.

Ускорение точки в неинерциальной системе отсчета можно в соответствии с (6.12) представить в виде:

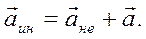(6.13)

Подставим выражение (6.13) в уравнение (6.11) и получим:

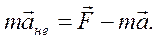(6.14)

Это и есть уравнение движения материальной точки относительно неинерциальной системы отсчета. Если в неинерциальной системе отсчета определять силу как вектор, равный произведению массы материальной точки на ее ускорение в этой системе отсчета, то правая часть уравнения (6.4) и является силой, действующей на материальную точку, движущуюся ускоренно в неинерциальной системе отсчета. Эта сила слагается из двух существенно различных составляющих. Первая оставляющая 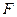является результатом взаимодействия тел и проявляется в инерциальной системе отсчета.

Совсем иной характер имеет составляющая – 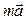. Она возникает не из-за взаимодействия тел, а из-за ускоренного движения системы отсчета. Она называется поступательной силой инерции. При переходе к другой ускоренно движущейся системе отсчета меняются и силы инерции. Эти силы инерции отличаются от настоящих сил, возникающих при взаимодействии тел. Второе отличие состоит в том, что силы инерции не подчиняются закону действия и противодействия (третьему закону Ньютона).

При описании движения тел относительно ускоренно движущейся поступательно системы отсчета наряду с силами, обусловленными взаимодействием тел друг с другом, необходимо учитывать так называемые силы инерции 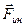. Эти силы следует полагать равными произведению массы тела на взятое с обратным знаком ускорение движущейся неинерциальной системы отсчета относительно инерциальной системы:

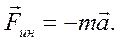(6.15)

Соответственно, уравнение движения в неинерциальной системе отсчета будет иметь вид

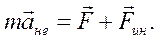(6.16)

Существует много явлений, которые могут быть интерпретированы как проявление силы инерции. Когда поезд набирает скорость, пассажиры в вагоне испытывают действие силы, направленной против движения поезда. Это и есть сила инерции. Силы инерции вызывают перегрузки, действующие на летчика при больших ускорениях самолета. Если в ускоренно движущемся вагоне висит шарик массы m, то сила инерции отклоняет его в сторону, противоположную ускорению (рисунок 6.6).

Нить отклоняется на такой угол, чтобы результирующая двух сил 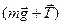, сообщала шарику r ускорение a, с которым движется вагон. Относительно системы отсчета, связанной с вагоном, шарик покоится. Это можно объяснить, если ввести силу инерции

,

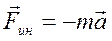уравновешивающую результирующую двух сил и .

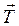Введение сил инерции дает возможность описывать движениетел в любых системах отсчета с помощью одних и тех же уравнений движения.

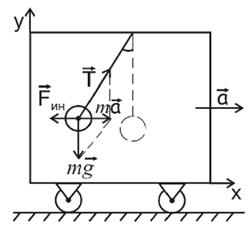
Рисунок 6.6 – К понятию силы инерции

Силы инерции имеют характерные особенности: они не отражают взаимодействие тел, а обусловлены характером неинерциальных систем отсчета, поэтому для сил инерции неприменим третий закон Ньютона. Характерным свойством сил инерции является их пропорциональность массе тела. Благодаря этому свойству силы инерции оказываются аналогичными силам тяготения. Движение тел под действием сил инерции сходно с движением в гравитационном поле. В качестве примера можно привести не-

весомость, возникающую в свободно падающем лифте. В свободно падающем лифте вес G тела массой m всегда равен нулю: 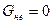. Действительно: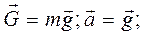

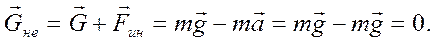(6.17)

Рассмотрим силы инерции, возникающие во вращающихся системах отсчета.