Двоичные циклические коды
Вышеприведенная процедура построения линейного кода имеет ряд недостатков. Она неоднозначна (МДР можно задать различным образом) и неудобна в реализации в виде технических устройств. Этих недостатков лишены линейные корректирующие коды, принадлежащие к классу циклических.
Циклическими называют линейные (n,k)-коды, обладающие следующим свойством: для любого кодового слова:
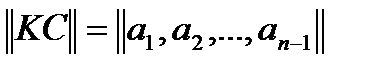 ;
;
существует другое кодовое слово:
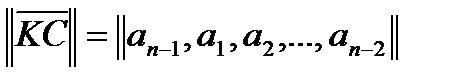 ,
,
полученное циклическим сдвигом элементов исходного кодового слова ||KC|| вправо или влево, и которое также принадлежит этому коду.
Для описания циклических кодов используют полиномы с фиктивной переменной. Будем обозначать эту переменную буквой Х.
Например, кодовое слово ||KC|| = ||011010|| .
Его можно описать полиномом
А(Х) = 0*Х5+1*Х4+1*Х3+0*Х2+1*Х1+0*Х0 .
Таким образом, разряды кодового слова в описывающем его полиноме используются в качестве коэффициентов при степенях фиктивной переменной Х.
Наибольшая степень фиктивной переменной Х в слагаемом с ненулевым коэффициентом называется степенью полинома. В вышеприведенном примере получился полином 4-й степени.
Теперь действия над кодовыми словами сводятся к действиям над полиномами. Вместо алгебры матриц здесь используется алгебра полиномов.
Рассмотрим алгебраические действия над полиномами, используемые в теории циклических кодов.
Суммирование полиномов разберем на примере С(Х) = А(Х) + В(Х).
Пусть ||A|| = ||011010||, ||B|| = ||110111||.
Тогда:
 A(X) A(X)
| = | + | X4 | + | X3 | + | + | X1 | + | |||
| B(X) | = | X5 | + | X4 | + | + | X2 | + | X1 | + | X0 | |
| C(X) | = | X5 | + | 0 | + | X3 | + | X2 | + | 0 | + | X0 |
Таким образом, при суммировании коэффициентов при Х в одинаковой степени результат берется по модулю 2. При таком правиле вычитание эквивалентно суммированию.
Умножение выполняется как обычно, но с использованием суммирования по модулю 2.
Рассмотрим умножение на примере умножения полинома (Х3+Х1+Х0) на полином (Х1+Х0).

| Х3 | + | + | Х1 | + | Х0 | ||

| Х1 | + | Х0 | |||||
| Х3 | + | + | Х1 | + | Х0 | |||
| Х4 | + | + | Х2 | + | Х1 | |||
| Х4 | + | Х3 | + | Х2 | + | + | Х0 |
Операция обратная умножению – деление. Деление полиномов выполняется как обычно, за исключением того, что вычитание выполняется по модулю 2 (вспомним, что вычитание по модулю 2 эквивалентно сложению по модулю 2).
Пример деления полинома (Х6+Х4+Х3) на полином (Х3+Х2+Х0):
| Х6 | + | 0 | + | Х4 | + | Х3 | + | 0 | + | 0 | + | 0 | Х3 | + | Х2 | + | 0 | + | Х0 | |
| Х6 | + | Х5 | + | 0 | + | Х3 |
| Х3 | + | Х2 | ||||||||||
| Х5 | + | Х4 | + | 0 | + | 0 | ||||||||||||||
| Х5 | + | Х4 | + | 0 | + | Х2 | ||||||||||||||
| 0 | + | Х2 | . |
Циклический сдвиг влево на одну позицию коэффициентов полинома степени n-1 получается путем его умножения на Х с последующим вычитанием из результата умножения полинома Xn+1, если его порядок 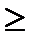 n. Последнее эквивалентно вычислению остатка от деления результата умножения на Xn+1.
n. Последнее эквивалентно вычислению остатка от деления результата умножения на Xn+1.
Проверим это на примере.
Пусть требуется выполнить циклический сдвиг влево на одну позицию коэффициентов полинома С(Х) = Х5+Х3+Х2+Х0.
В результате должен получиться полином 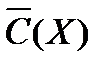 = Х4+Х3+Х1+Х0 .
= Х4+Х3+Х1+Х0 .
Это легко доказывается:
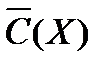 = С(Х)*Х-(Х6+1)=(Х6+Х4+Х3+Х1)+(Х6+Х0) = Х4+Х3+Х1+Х0 .
= С(Х)*Х-(Х6+1)=(Х6+Х4+Х3+Х1)+(Х6+Х0) = Х4+Х3+Х1+Х0 .
В основе циклического кода лежит образующий полином m-го порядка (напомним, что m – число дополнительных разрядов). Будем обозначать его gm(X).
Образование кодовых слов (кодирование) KC выполняется путем умножения информационного полинома (информационный полином – полином с коэффициентами, являющимися информационной последовательностью) Иi(X) порядка i<k на образующий полином:
КСm+i(Х) = gm(X) * Иi(X) .
Принятое кодовое слово может отличаться от переданного искаженными разрядами – результатом действия искажающих передаваемую информацию помех.
ПКС(Х) = КС(Х) + ВО(Х),
где ВО(Х) – полином вектора ошибки, а суммирование, как обычно, ведется по модулю 2.
Декодирование, как и раньше начинается с нахождения опознавателя, в данном случае в виде полинома ОП(Х). Этот полином вычисляется как остаток от деления полинома принятого кодового слова ПКС(Х) на образующий полином gm(X):
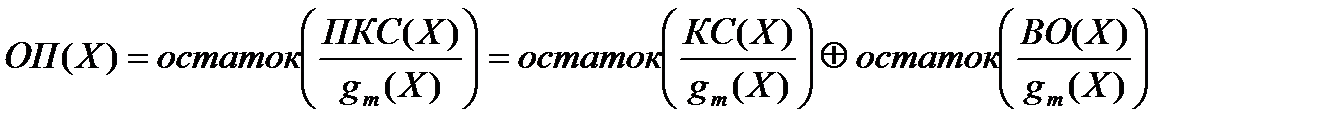 .
.
Первое слагаемое остатка не имеет, т.к. кодовое слово было образовано путем умножения полинома информационной последовательности на образующий полином. Следовательно, и в данном случае опознаватель полностью зависит от вектора ошибки.
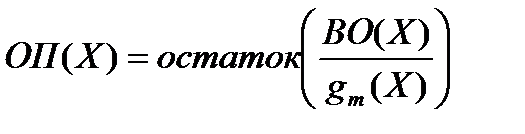 .
.
Образующий полином выбирается таким, чтобы при данном m как можно больше число отношений ВО(Х)/gm(Х) давало различные остатки.
Такому требованию отвечают так называемые неприводимые полиномы, которые не делятся без остатка ни на один полином степени m и ниже, кроме как сам на себя и на 1.
Приведенная здесь процедура образования кодового слова неудобна тем, что такой код получается несистематическим, т.е. таким, в кодовых словах которого нельзя выделить информационные и дополнительные разряды.
Этот недостаток был устранен.
Способ кодирования, приводящий к получению систематического линейного циклического кода, состоит в приписывании к информационной последовательности И дополнительных разрядов ДР.
Эти дополнительные разряды предлагается находить по следующей формуле:
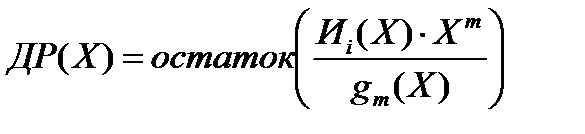
Порядок полинома ДР(Х) гарантировано меньше m (поскольку это остаток).
Приписывание дополнительных разрядов к информационной последовательности, используя алгебру полиномов, можно описать формулой:
KC(X) = И(Х)*Хm + ДР(Х)
Одним из свойств циклических линейных кодов является то, что результат деления любого разрешенного кодового слова КС на образующий полином g также является разрешенным кодовым словом.
Докажем, что получаемые по вышеприведенному алгоритму кодовые слова являются кодовыми словами циклического линейного кода. Для этого нужно убедиться в том, что произвольное разрешенное кодовое слово делится на образующий полином без остатка:
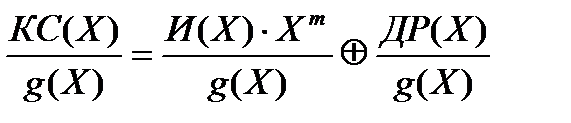 .
.
Рассмотрим первое слагаемое: 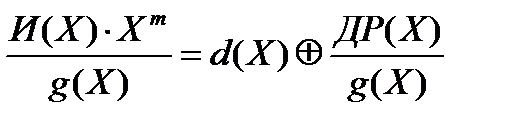 ,
,
где d(X) – целая часть результата деления.
Подставим полученную сумму на место первого слагаемого:
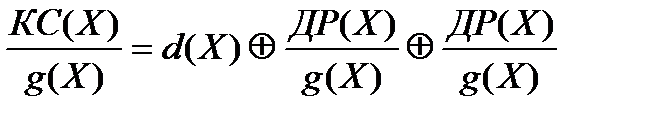 .
.
Суммирование последних двух слагаемых дает нулевой результат (напомним, что суммирование выполняется по модулю 2).
Значит 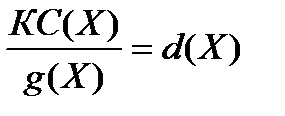 − целая часть деления. Остатка нет. Это означает, что описанный выше способ кодирования соответствует циклическому коду.
− целая часть деления. Остатка нет. Это означает, что описанный выше способ кодирования соответствует циклическому коду.
Дата добавления: 2021-04-21; просмотров: 657;











