Некоторые свойства циклических кодов
Все свойства циклических кодов определяются образующим полиномом.
1. Циклический код, образующий полином которого содержит более одного слагаемого, обнаруживает все одиночные ошибки.
Строго доказывать это не будем. Покажем это на примере простейшего образующего полинома g(x)=X+1. Вектор однократной ошибки в i-м разряде описывается полиномом ВО(Х)=Хi.
Найдем опознаватель 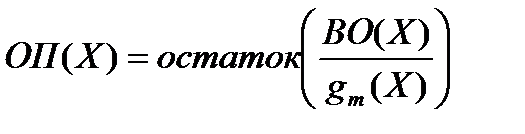 :
:
| Хi | + | + | +. | . | . | + | X | + | ||||||||||
| Xi | + | Xi-1 | Xi-1 | + | Xi-1 | +. | . | . | + | |||||||||
| Xi-1 | + | |||||||||||||||||
| Xi-1 | + | Xi-2 | ||||||||||||||||
| Xi-2 | ||||||||||||||||||
| . | ||||||||||||||||||
| . | ||||||||||||||||||
| X | ||||||||||||||||||
| X | + |
| ||||||||||||||||
Таким образом, поскольку ВО имеет вес 1 (не равен нулю) ошибка обнаруживается.
2. Докажем теперь, что циклический код, образованный при помощи полинома g(X)=X+1, позволяет обнаруживать не только одиночные но и любые ошибки нечетной кратности.
Доказательство.
Рассмотрим первый вариант кодирования – кодирование по формуле:
КС(Х)=И(Х)*g(X) .
В нашем случае g(X)=X+1.
После подстановки получим:
КС(Х)=И(Х)*(X+1)=Х*И(Х)+И(Х) .
Если И(Х) содержит L единичных коэффициентов, то и Х*И(Х) тоже содержит столько же L единичных коэффициентов, но при степенях Х на единицу больших. Обозначим L’ количество единичных коэффициентов при одинаковых степенях Х. Оба полинома согласно формуле следует сложить. При сложении члены полиномов с одинаковыми степенями и единичными коэффициентами в сумме дадут слагаемые с нулевыми коэффициентами (сложение по модулю 2). В общем, в сложении будет участвовать 2L слагаемых с единичными коэффициентами, 2L’ из которых попарно взаимно уничтожаются.
В суммарном полиноме останется в итоге 2L-2L’=2(L-L’) членов с единичными коэффициентами – четное число. Таким образом, при использовании образующего полинома Х+1 получаемые в результате кодовые слова обязательно имеют четное число единичных разрядов. Любое искажение с нечетным числом ошибок преобразует разрешенное кодовое слово с четным числом разрядов в запрещенное – с нечетным. Такое кодовое слово, поскольку оно является запрещенным, сразу же будет обнаружено по наличию остатка от его деления на образующий полином.
Надо заметить, что коды, обнаруживающие четное количество ошибок, используются довольно часто.
Найдем теперь для случая применения образующего полинома Х+1 упрощенный вариант процедуры кодирования.
Ранее была приведена следующая формула получения кодового слова (случай систематического кода):
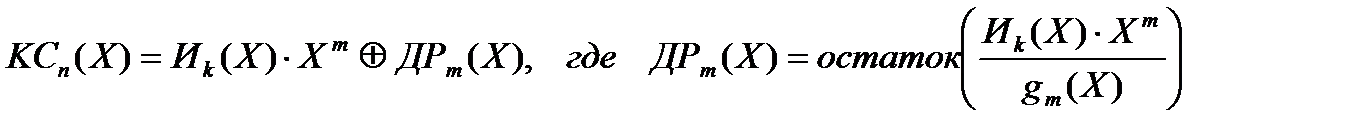 .
.
Остатком от деления любого полинома на Х+1 может быть либо 0 (остатка нет) либо 1. Следовательно, m=1, т.е. 1 разряд.
Учитывая вывод о том, что при использовании образующего полинома Х+1 получаемые в результате кодовые слова обязательно имеют четное число единичных разрядов, делаем вывод, что этот один разряд должен дополнять количество единиц в информационной последовательности до четного числа. В этом и заключается упрощенный способ кодирования при использовании разделимого циклического кода с образующим полиномом Х+1.
3. Циклический код, образованный полиномом gm(X), обнаруживает все двукратные и однократные ошибки, если значность кода n меньше или равна степени L полинома XL+1, где L – наименьшее число, при котором XL+1 делится на gm(X) без остатка.
Доказательство не приводим.
Дата добавления: 2021-04-21; просмотров: 464;











