Матричное описание циклических кодов

Циклические коды можно, как и любые линейные коды, описывать с помощью матриц.

Вспомним, что KC(X) = g_m(X)*И(Х) .

Вспомним также на примере порядок умножения полиномов:

g_m(X) = 1 0 1 0 1 1

И(Х) = 1 0 1 1

1 0 1 0 1 1 * 1

1 0 1 0 1 1 * 1

1 0 1 0 1 1 * 0

1 0 1 0 1 1 * 1

1 0 0 1 0 0 1 0 1

Это соответствует описанному выше упрощенному способу умножения матриц:

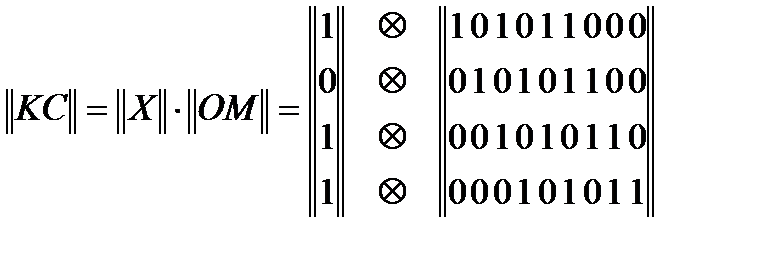
Видно, что, если в качестве строк образующей матрицы взять наборы сдвинутых вправо коэффициентов образующего полинома, вычисление кодовых слов при помощи матриц полностью эквивалентно вычислению кодовых слов при помощи полиномов.

Согласно второму способу кодирования, позволяющего получить систематический код, кодовое слово находится по формуле:

.

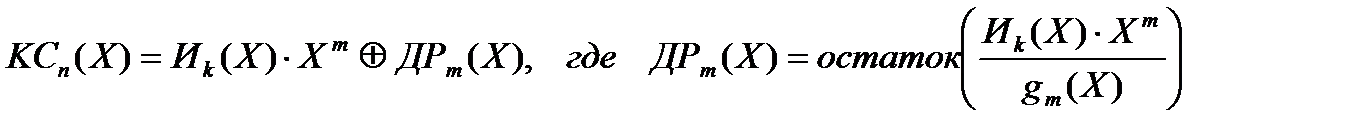Образующая матрица ||ОМ|| в этом случае должна состоять из 2 частей – единичной матрицы ||I|| и матрицы дополнительных разрядов ||МДР||: ||OM|| = || I МДР || .

Результат кодирования при помощи матриц будет совпадать с результатом кодирования при помощи полиномов в том случае, если строки матрицы дополнительных разрядов образовать по следующей формуле:

.

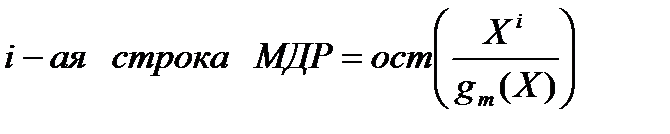Далее по МДР легко построить ТПМ, найти опознаватели и пользоваться описанными выше для линейных кодов процедурами кодирования-декодирования.