Порядок декодирования

В результате передачи кодового слова через канал оно может быть искажено помехой. Это приведет к тому, что принятое кодовое слово ||ПКС|| может не совпасть с исходным ||КС||.

Искажение можно описать с помощью следующей формулы:

||ПКС|| = ||KC|| + ||BO||,

где ||BO|| − вектор ошибки – матрица-строка размерностью 1*n, с 1 в тех разрядах, в которых произошли искажения.

Декодирование основано на нахождении так называемого опознавателя – матрицы-строки ||ОП_1*m|| длиной m разрядов (m – количество добавочных или избыточных разрядов в кодовом слове). Опознаватель используется для нахождения предполагаемого вектора ошибки.

Опознаватель находят по следующей формуле:

||ОП|| = ||ПКС|| * ||ТПМ||,

где ||ПКС|| – принятое и возможно искаженное кодовое слово;

||ТПМ|| - транспонированная проверочная матрица, которая получается из матрицы добавочных разрядов ||МДР|| путем приписывания к ней снизу единичной матрицы:

.

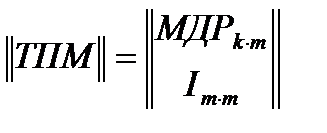Пример ||ТПМ||:

||1 1 0||

||1 1 1||

||0 1 1||

||1 0 1||

||1 0 0||

||0 1 0||

||0 0 1||

Поскольку ||ПКС|| = ||KC|| + ||BO||, последнюю формулу можно записать в виде: ||ОП|| = ||KC|| * ||ТПМ|| + ||BO|| * ||ТПМ||

Рассмотрим первое слагаемое.

||КС|| − матрица-строка, причем первые k разрядов – информационные.

Докажем теперь, что произведение кодового слова ||КС|| на ||ТПМ|| приводит к получению нулевой матрицы ||0||.

Поскольку ||KC|| − матрица-строка, возможен упрощенный порядок умножения матриц, рассмотренный выше.

.

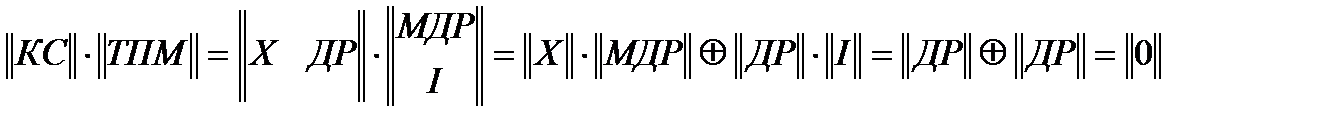Следовательно, первое слагаемое в ||ОП|| = ||KC|| * ||ТПМ|| + ||BO|| * ||ТПМ|| всегда равно нулю и опознаватель полностью зависит от вектора ошибки ||BO||.

Если теперь подобрать такую матрицу ТПМ, а значит и МДР, чтобы разным векторам ошибки соответствовали разные опознаватели ОП, то по этим опознавателям можно будет находить вектор ошибки ВО, а значит и исправлять эти ошибки.

Соответствие опознавателей векторам ошибки находится заранее путем перемножения векторов исправляемых ошибок на ТПМ:

||ОП|| = ||BO|| * ||ТПМ||

Таким образом, способность кода исправлять ошибки целиком определяется МДР.

Найдем способ построения МДР для кодов, исправляющих однократные ошибки.

Число столбцов m определяется, как показано выше, в виде минимального числа, удовлетворяющего неравенству 2^m > m+k .

Так как ВО для случая исправления одной ошибки может иметь лишь одну единицу, таких ВО может быть только n (1 в различных разрядах). Учитывая возможность использования в данном случае вышеописанного упрощенного способа перемножения матриц, видим, что опознаватели в этом случае просто совпадают со строками ТПР, причем номер строки равен номеру искаженного разряда.

Для того, чтобы ни одна строка МДР не совпадала со строкой приписанной к ней ниже единичной матрицы, число единичных разрядов в МДР должно быть больше одного. Кроме того, чтобы строки не были одинаковыми (а они совпадают с опознавателями; опознаватели различных ошибок должны быть различны) они должны отличаться не менее, чем в одном разряде.

Эти правила можно получить и другим способом.

Кодовое расстояние для кода, исправляющего до КСК ошибок, вычисляется по формуле КСК = int[(d_min-1)/2]. Несложно найти, что d_min=3 при КСК=1.

Для линейных кодов справедливо утверждение о том, что кодовое расстояние линейного кода равно минимальному весу кодового слова этого кода. Для доказательства вспомним определение линейного кода, согласно которому линейными называются коды любые линейные комбинации кодовых слов которых также являются кодовыми словами. Для определения расстояния между кодовыми словами нужно найти вес их суммы. Но эта сумма сама является кодовым словом. Кодовое же расстояние равно минимальному расстоянию между кодовыми словами. Это тоже кодовое слово.

При кодировании мы суммируем определенное количество (обозначим это количество буквой i) строк образующей матрицы ОМ. За счет единичной матрицы в полученном таким образом кодовом слове будет как минимум i единиц.

Если i=1 (i не может быть меньше 1), то кодовое слово совпадает с одной из строк ОМ, а поскольку минимальный вес кодового слова в нашем случае равен 3, за счет МДР должно быть добавлено еще две единицы. Отсюда требование наличия не менее чем двух единиц в каждой строке МДР.

Если i=2, 2 единицы получаем за счет единичной матрицы и, чтобы получить еще одну единицу, нужно иметь хотя бы одно различие между двумя любыми строчками МДР.

Полученный нами код не удобен тем, что опознаватель, хотя и связан однозначно с номером искаженного разряда, как число не равен ему. Для поиска искаженного разряда нужно использовать дополнительную таблицу соответствия между опознавателем и этим номером. Коды, в которых такое соответствие присутствует, были найдены и получили название кодов Хэмминга.

Построение МДР для случая исправления многократных ошибок значительно усложняется. Разными авторами были найдены различные алгоритмы построения МДР для этого случая, а соответствующие коды называются их именами.

Несколько слов об обозначении кодов.

Равномерные блоковые систематические коды имеющие n-разрядные кодовые слова с k информационными разрядами называют (n,k)-кодами.

В качестве примера в лекции рассмотрен код (8,4).

||OM||   ||1 0 0 0 1 1 0|| ||0 1 0 0 1 1 1|| ||0 0 1 0 0 1 1|| ||0 0 0 1 1 0 1||

При использовании линейных кодов можно избежать применения операций над матрицами. Рассматривая процесс кодирования, нетрудно заметить, что определенные добавочные разряды получаются путем сложения по модулю 2 определенных информационных разрядов.

||ТПМ||   ||1 1 0|| ||1 1 1|| ||0 1 1|| ||1 0 1|| ||1 0 0|| ||0 1 0|| ||0 0 1||

Обозначим кодовое слово X₁X₂…X_kY₁Y₂…Y_m. Здесь Х – информационные разряды, Y – добавочные разряды.

В нашем примере

k=4, M=3,

Y₁ = X₄ , Y₂ = X₁+X₂+X₄ ,

Y₃ = X₁+X₂+X₃ ,

Y₄ = X₂+X₃+X₄ .

Для расчета разрядов Z опознавателя также можно использовать соответствующие формулы:

Z₁ = F1+F2+F4+F5

Z₂ = F1+F2+F3+F6

Z₃ = F2+F3+F4+F7,

Где Fi – разряды ТПМ

Расчеты по формулам широко используются при построении кодирующих и декодирующих устройств.