Определение числа добавочных разрядов m.

Для определения числа добавочных разрядов можно воспользоваться формулой границы Хэмминга:

.

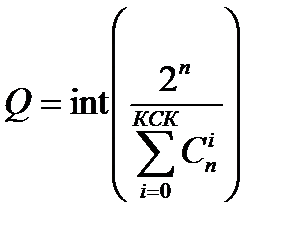При этом можно получить плотноупакованный код, т.е. код с минимальной при заданных параметрах кода длиной n кодового слова и, следовательно, избыточностью.

К задаваемым параметрам кода относятся: длина информационной последовательности k и корректирующая способность кода КСК.

При k информационных двоичных разрядах может передаваться 2^k кодовых слов. Если приравнять Q=2^k, то с учетом границы Хэмминга получаем: .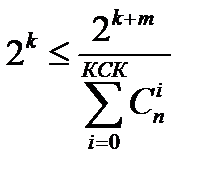

Если КСК=1, т.е. строится код, исправляющий максимум однократные ошибки, то ,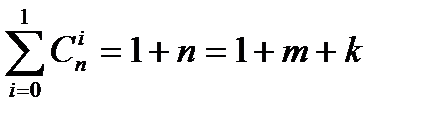

так как 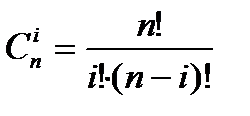и .

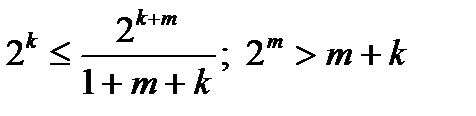С учетом последней формулы ищется наименьшее m при котором удовлетворяется это неравенство. Наименьшее потому, что при этом достигается наименьшая избыточность.

Пример: k=7, тогда путем простого перебора легко найти, что m=4.

2. Построение образующей матрицы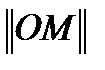

Линейные коды обладают следующим свойством: из всего множества 2^k разрешенных кодовых слов, образующих, кстати, группу, можно выделить подмножества из k слов, обладающих свойством линейной независимости.

Линейная независимость означает, что никакое из слов, входящих в подмножество линейно-независимых кодовых слов, нельзя получить путем суммирования (с помощью линейного выражения) любых других слов, входящих в это подмножество.

В то же время любое другое из разрешенных кодовых слов можно получить путем суммирования определенных линейно-независимых слов.

Таким образом, построение кодовых комбинаций линейного кода связано с линейными операциями. Для выполнения таких операций удобно пользоваться хорошо разработанным аппаратом матричных вычислений.

Для образования кодовых слов по информационной последовательности (кодирования) используют матрицу, называющуюся образующей.

Образующая матрица получается путем записи в столбец k линейно-независимых слов.

Обозначим кодируемую информационную последовательность X и будем записывать ее в виде матрицы-строки 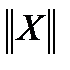размерностью 1*k, например: 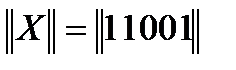, где k=5 .

Один из способов построения образующей матрицы следующий:

Она строится из единичной матрицы ||I|| размерностью k*k и приписанной к ней справа матрицы добавочных (избыточных) разрядов ||МДР|| размерности k*m:

||ОМ_k*n|| = ||I_k*k МДР_k*m||,

где при k=4 .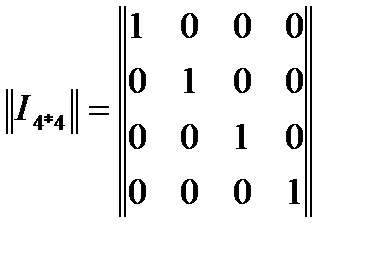

Такая структура ОМ обеспечивает получение систематического кода.

Порядок построения матрицы МДР будет рассмотрен ниже.