Лемма 2. Об оптимальности префиксного кода нередуцированного ансамбля, если префиксный код редуцированного ансамбля оптимален

Формулировка. Если некоторый префиксный код редуцированного ансамбля U'является оптимальным, то соответствующий ему префиксный код исходного ансамбля также является оптимальным.

Доказательство

Заметим, что нередуцированный код от редуцированного отличается только заменой одного кодового слова редуцированного кода двумя кодовыми словами нередуцированного. Все же остальные кодовые слова этих кодов совпадают. Кроме того, поскольку согласно формулировке леммы редуцированный код оптимален, средняя длина его кодовых слов минимальна. Если удастся доказать, что замена одного кодового слова редуцированного кода двумя кодовыми словами нередуцированного приводит к минимальному увеличению средней длины кодового слова нередуцированного кода, то эта средняя длина также является минимально возможной и, следовательно, полученный таким образом нередуцированный код является оптимальным.

Для доказательства запишем выражения для средней длины кодовых слов редуцированного и нередуцированного кода.

Средняя длина нередуцированного кода:

,

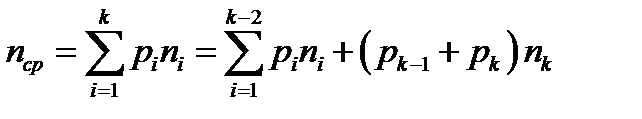поскольку, согласно лемме 1, два последних кодовых слова двоичного оптимального кода имеют одинаковую длину и отличаются символом последнего разряда.

Средняя длина редуцированного кода:

.

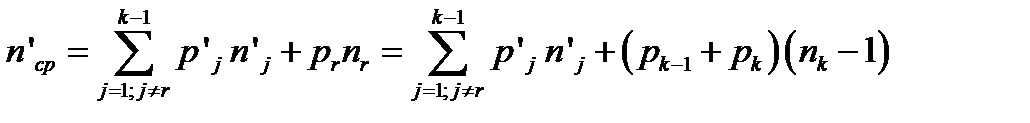Здесь r − номер кодового слова редуцированного кода, полученного путем объединения двух последних кодовых слов исходного нередуцированного кода. Надо учесть, что после этого все кодовые слова редуцированного кода переупорядочиваются в порядке убывания вероятностей, а r – номер объединенного кодового слова после этого упорядочения.

Новое кодовое слово получается из кодовых слов, которые оно заменяет путем отбрасывания последнего разряда, которым они отличаются друг от друга. Поэтому его длина на 1 меньше.

Теперь найдем изменение средней длины :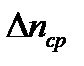

.

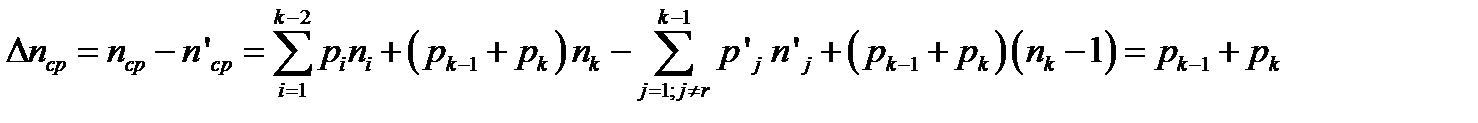Это приращение минимально, так как p_k-1 и p_k – наименьшие вероятности. Это и доказывает лемму 2.

Задача построения оптимального кода теперь сводится к построению последовательности редуцированных ансамблей:

.

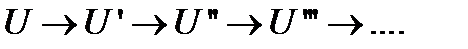При каждой редукции (уменьшении) число букв в первичном алфавите уменьшается на 1 букву и наступает момент, когда в результате редуцирования останутся только 2 буквы. Оптимальный код для такого ансамбля очевиден – 0 для одной буквы и 1 − для другой. Дальше, двигаясь в обратном направлении ( 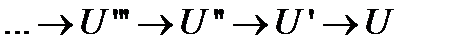), переходя от оптимального кода редукции более высокого порядка к оптимальному коду редукции менее высокого порядка, что можно делать согласно лемме 2, можно дойти до оптимального кода исходного ансамбля U.

3.7.3. Коды Хаффмена[12]

На этом алгоритме построена процедура построения оптимального кода, предложенная в 1952 году Хаффменом:

1) буквы первичного алфавита выписываются в основной столбец в порядке убывания вероятностей;

2) две последние буквы объединяются в одну вспомогательную букву, которой приписывается суммарная вероятность;

3) вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются;

4) процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Методика поясняется примером, представленным табл. 3.2.

Таблица 3.2.

Для составления кодовой комбинации, соответствующей данному сообщению, необходимо проследить путь перехода вероятности сообщения по строкам и столбцам таблицы.

Для наглядности строится кодовое дерево. Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваивается символ 1, а с меньшей − 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до каждой буквы. Кодовое дерево для алфавита букв, рассматриваемого в таблице, изображено на рис. 3.3.

Рис. 3.3. Кодовое дерево.

Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию (табл. 3.3).

Таблица 3.3

3.7.4. Коды Шеннона−Фэно

Ранее, независимо друг от друга Шенноном и Фэно[13] была предложена другая процедура построения эффективного кода. Получаемый при ее помощи код называют кодом Шеннона−Фэно.

Код Шеннона−Фэно строится следующим образом:

1) буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей;

2) затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы;

3) всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним 0;

4) каждая из полученных групп, в свою очередь, разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. ;