Лемма 1. О существовании оптимального кода с одинаковой длиной кодовых слов двух наименее вероятных кодируемых букв

Формулировка. Для любого источника с k>=2 буквами существует оптимальный (в смысле минимума средней длины кодового слова) двоичный код, в котором два наименее вероятных слова x_k и x_k-1 имеют одну и ту же длину и отличаются лишь последним символом.

Пример: если существует кодовое слово x_k = 0 1 1 0 0 0 1 0,

то существует и кодовое слово x_k-1 = 0 1 1 0 0 0 1 1

Доказательство.

1. Докажем сначала, что для оптимального кода 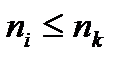, где i < k , т.е. последнее кодовое слово, имеющее, кстати, наименьшую вероятность появления, имеет наибольшую длину.

Для доказательства этого вспомним, что .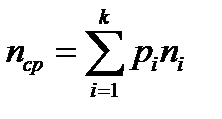

Найдем на сколько изменится n_ср, если n_k=n_max и попытаемся поменять его с любым другим j-м словом длиной n_j, т.е. a_j кодировать x_k и a_k кодировать x_j.

После такой перестановки получим:

,

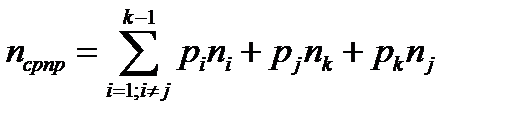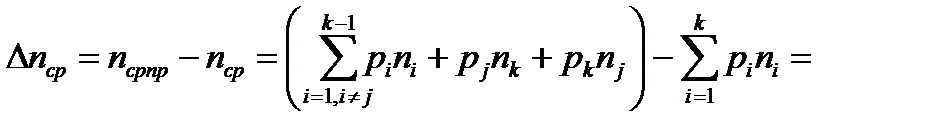
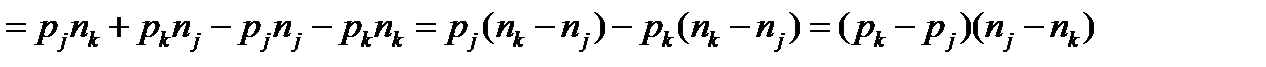. (3.4)

Если код оптимален, то любая перестановка кодовых слов должна приводить с росту средней длины кодового слова – к тому, что 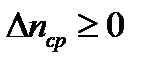и к превращению кода из оптимального в неоптимальный.

Докажем, что при принятых нами условиях действительно .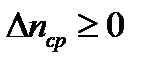

Поскольку, согласно постулированному[10] условию, буквы первичного алфавита упорядочены в порядке убывания вероятностей, разность 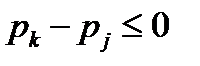. С другой стороны, 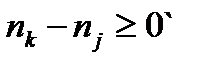, тогда, когда 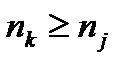, что и требовалось доказать.

2. Заметим далее, что в любом оптимальном префиксном коде, для которого n_k=n_max, должно быть другое кодовое слово, отличающееся от n_k только буквой в последнем разряде. Например, если x_k = 10110, то должно еще быть слово x_i = 10111. Это следует из того, что в противном случае этот последний разряд можно было бы отсечь без нарушения свойства префикса и n_ср уменьшилось бы, что для оптимального кода невозможно. Следовательно, кодовое слово, отличающееся только последним разрядом, должно существовать.

3. Наконец, если x_i отличается от x_k только в одной позиции, то n_i=n_k и, как следует из (1), x_i и x_k-1 можно поменять меcтами без увеличения n_ср.

Таким образом, нами доказано, что кодовые слова x_k и x_k-1 оптимального префиксного кода имеют одинаковую и максимальную длину n_k=n_k-1 и отличаются лишь одной буквой вторичного алфавита.

С помощью этой леммы решение задачи построения оптимального кода сводится к решению задачи построения кодовых слов x₁, x₂, … , x_k-2 и отысканию первых n_k-1 символов кодового слова x_k.

Следуя принятой терминологии, назовем совокупность {a} букв первичного алфавита, упорядоченных в порядке убывания вероятностей появления и вероятностей {p} их появления ансамблем U.

Определим теперь редуцированный[11] ансамбль U' как ансамбль, полученный из исходного нередуцированного ансамбля путем замены двух последних (с наименьшей вероятностью) букв исходного ансамбля одной новой буквой редуцированного ансамбля.

Таким образом, редуцированный ансамбль отличается от исходного нередуцированного меньшим на одну букву количеством букв первичного алфавита. Все буквы редуцированного ансамбля, кроме одной совпадают с буквами исходного ансамбля. Одна же буква редуцированного ансамбля заменяет две последние (с наименьшей вероятностью появления) буквы исходного ансамбля. Вероятность появления этой новой буквы редуцированного ансамбля при такой замене естественно равна сумме вероятностей появления двух букв исходного ансамбля, которые она заменяет.

Буквы алфавита редуцированного ансамбля так же, как буквы алфавита нередуцированного ансамбля, упорядочиваются в порядке убывания вероятностей их появления в сообщении. В результате такого упорядочения положение даже одних и тех же букв в исходном и редуцированном ансамбле может быть различным.

Любой префиксный код редуцированного ансамбля U', можно превратить в код исходного ансамбля простым добавлением концевого символа 0 к кодовому слову x'_k-1 символа 1 к кодовому слову x'_k. Это устанавливает взаимно однозначное соответствие между множеством префиксных кодов редуцированного ансамбля U' и множеством префиксных кодов исходного ансамбля U.