Алгоритм на псевдокоде
Пузырьковая сортировка
Обозначим i – номер итерации,
j – индекс правого элемента в текущей паре.
DO (i= 1, 2, ... n-1)
DO (j= n, n-1, ... i+1)
IF (aj < aj-1) aj ↔ aj-1 FI
OD
OD
Проанализируем сложность пузырьковой сортировки. Количество сравнений в методе прямого выбора и в методе пузырьковой сортировки одинаково и не зависит от исходной отсортированности массива. Однако количество пересылок M зависит от того, как часто выполняется условие aj < aj-1. Можно определить максимальное и минимальное значения Мmin £ Mсред £ Mmax,. где
Мmin = 0, при сортировке упорядоченного по возрастанию массива.
Mmax = 3C = 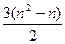 , при сортировке упорядоченного по убыванию массива.
, при сортировке упорядоченного по убыванию массива.
Отсюда следует, что Mсред=О(n2), при n®¥
Таким образом, пузырьковая сортировка сильно зависит от исходной упорядоченности массива по количеству сравнений. Метод обеспечивает устойчивую сортировку.
2.3 Шейкерная сортировка
Анализируя метод пузырьковой сортировки можно отметить два обстоятельства. Во-первых, если при движении по части массива перестановки не происходят, то эта часть массива уже отсортирована и, следовательно, ее можно исключить из рассмотрения. Во-вторых, при движении от конца массива к началу минимальный элемент «всплывает» на первую позицию, а максимальный элемент сдвигается только на одну позицию вправо. Эти две идеи приводят к следующим модификациям в методе пузырьковой сортировки. Границы рабочей части массива (т.е. части массива, где происходит движение) устанавливаются в месте последнего обмена на каждой итерации. Массив просматривается поочередно справа налево и слева направо.
Пример.Отсортировать слово методом шейкерной сортировки. Подчёркнуты те пары, в которых произошёл обмен. Вертикальной чертой ограничена рабочая часть массива.
| К | У | Р | А | П | О | В | А |
| А | В | ||||||
| А | О | ||||||
| А | П | ||||||
| А | А | ||||||
| А | Р | ||||||
| А | У | ||||||
| А | К | ||||||
| А | К | У | Р | А | П | О | В |
| К | У | ||||||
| Р | У | ||||||
| А | У | ||||||
| П | У | ||||||
| О | У | ||||||
| В | У | ||||||
| А | К | Р | А | П | О | В | У |
| В | О | ||||||
| В | П | ||||||
| А | В | ||||||
| А | Р | ||||||
| А | К | ||||||
| А | А | К | Р | В | П | О | У |
| К | Р | ||||||
| В | Р | ||||||
| П | Р | ||||||
| О | Р | ||||||
| А | А | К | В | П | О | Р | У |
| О | П | ||||||
| В | О | ||||||
| В | К | ||||||
| А | А | В | К | О | П | Р | У |
| К | О | ||||||
| О | П | ||||||
| А | А | В | К | О | П | Р | У |
Рисунок 4 Шейкерная сортировка
Алгоритм на псевдокоде
Метод шейкерной сортировки
Обозначим
L – левая граница рабочей части массива.
R – правая граница рабочей части массива.
n – количество элементов в массиве
L: = 1, R: = n, k: = n,
DO
DO (j =R, R-1, ... L+1)
IF (aj < aj-1) aj ↔ aj-1, k: = j FI
OD
L: = k
DO (j: = L, L+1, ... R-1)
IF (aj > aj+1) aj ↔ aj+1, k: = j, FI
OD
R: = k
OD (L < R)
Оценим трудоемкость метода. Количество пересылок такое же, как и в методе пузырьковой сортировки Mсред=О(n2), при n®¥. Улучшения в методе шейкерной сортировки приводят к снижению количества сравнений. Точное выражение для величины С получить не удается, поэтому определим границы, в которых изменяется С. Если сортируется массив, в котором элементы расположены в порядке возрастания, то в методе шейкерной сортировки достаточно один раз просмотреть массив. Тогда Сmin = n-1, где n – количество элементов в массиве. Если массив отсортирован в обратном порядке, то на каждой итерации границы слева и справа сдвигаются на одну позицию и Сmax = 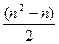 . Следовательно, Ссред=О(n2), при n®¥. Таким образом, как и пузырьковая сортировка, метод шейкерной сортировки сильно зависит от исходной упорядоченности массива по количеству сравнений. Метод обеспечивает устойчивую сортировку.
. Следовательно, Ссред=О(n2), при n®¥. Таким образом, как и пузырьковая сортировка, метод шейкерной сортировки сильно зависит от исходной упорядоченности массива по количеству сравнений. Метод обеспечивает устойчивую сортировку.
2.4 Варианты заданий
1. Разработать процедуру сортировки массива целых чисел методом прямого выбора (язык программирования Паскаль или Си). Правильность сортировки проверить путем подсчета контрольной суммы и числа серий в массиве. Предусмотреть подсчет количества пересылок и сравнений (М и С), сравнить их с теоретическими оценками.
2. В методе прямого выбора придумать способ устранения фиктивных перестановок и оценить его влияние на общую трудоемкость метода сортировки.
3.Разработать процедуру построения графика зависимости величин М и С от размера массива.
4. Разработать процедуру сортировки массива целых чисел методом пузырьковой сортировки (язык программирования Паскаль или Си). Правильность сортировки проверить путем подсчета контрольной суммы и числа серий в массиве. Предусмотреть подсчет количества пересылок и сравнений (М и С), сравнить с теоретическими оценками.
5. Разработать процедуру сортировки массива целых чисел методом шейкерной сортировки (язык программирования Паскаль или Си). Правильность сортировки проверить путем подсчета контрольной суммы и числа серий в массиве. Предусмотреть подсчет количества пересылок и сравнений (М и С), сравнить с теоретическими оценками.
6. Сравнить трудоемкости пузырьковой и шейкерной сортировок на массивах убывающих, случайных и возрастающих чисел.
7. Сравнить трудоемкости метода прямого выбора и шейкерной сортировки на массивах убывающих, случайных и возрастающих чисел.
3. Метод Шелла
3.1 Метод прямого включения
Сначала рассмотрим метод сортировки, который является базовым для метода Шелла. Метод прямого включения заключается в следующем. Начиная с i = 2, i=2,… n, берём очередной i–й элемент массива и включаем его на нужное место среди первых (i-1) элементов, при этом все элементы, которые больше ai сдвигаются на одну позицию вправо.
Пример. Отсортировать слово методом прямого включения.
Условные обозначения
X i-тый элемент
X сравнение элемента X с i-тым элементом
 сдвиг элемента на одну позицию вправо
сдвиг элемента на одну позицию вправо
| К | У | Р | А | П | О | В | А |
 К К
| У | Р | А | П | О | В | А |
| К | Р | У | А | П | О | В | А |
| А | К | Р | У | П | О | В | А |
| А | К | П | Р | У | О | В | А |
| А | К | О | П | Р | У | В | А |
| А | В | К | О | П | Р | У | А |
| А | А | В | К | О | П | Р | У |
Рисунок 5 Метод прямого включения
Дата добавления: 2022-02-05; просмотров: 590;











