Алгоритм на псевдокоде
Метод прямого выбора
DO (i = 1, 2, ... n-1)
k:=<номер наименьшего элемента из ai,… an>
ai ↔ ak
OD
Дадим оценку трудоёмкости метода прямого выбора. В данном случае можно найти точные выражения для М и С. Поскольку на каждой итерации происходит точно один обмен, то M = 3(n-1). Определим теперь количество сравнений. На первом этапе имеем (n-1) сравнений, на втором – (n-2) сравнений, на i-том этапе происходит (n- i) сравнений и т.д. Суммируя, получим C = 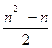
Отметим важные особенности метода прямого выбора. Метод не зависит от исходной отсортированности массива, т.е. значения М и С не меняются, даже если сортируется уже отсортированный массив. Сортировка методом прямого выбора неустойчива.
2.2 Пузырьковая сортировка
Популярный метод пузырьковой сортировки заключается в следующем. Двигаясь от конца массива к его началу, будем сравнивать между собой соседние элементы. При этом если правый элемент aj будет меньше чем левый aj-1, j=n, n-1, … ,2, то поменяем их местами. Таким образом, при первом проходе наименьший элемент переместится на первое место и можно не учитывать его при сортировке оставшейся части массива. При втором проходе наименьший элемент из оставшихся “всплывёт” на второе место. Через (n-1) итераций массив будет отсортирован.
Пример.Отсортировать слово методом пузырьковой сортировки. Подчёркнуты те пары, в которых произошёл обмен. Вертикальной чертой ограничена отсортированная часть массива.
| К | У | Р | А | П | О | В | А |
| А | В | ||||||
| А | О | ||||||
| А | П | ||||||
| А | А | ||||||
| А | Р | ||||||
| А | У | ||||||
| А | К | ||||||
| А | К | У | Р | А | П | О | В |
| В | О | ||||||
| В | П | ||||||
| А | В | ||||||
| А | Р | ||||||
| А | У | ||||||
| А | К | ||||||
| А | А | К | У | Р | В | П | О |
| О | П | ||||||
| В | О | ||||||
| В | Р | ||||||
| В | У | ||||||
| В | К | ||||||
| А | А | В | К | У | Р | О | П |
| О | П | ||||||
| О | Р | ||||||
| О | У | ||||||
| К | О | ||||||
| А | А | В | К | О | У | Р | П |
| П | Р | ||||||
| П | У | ||||||
| О | П | ||||||
| А | А | В | К | О | П | У | Р |
| Р | У | ||||||
| П | Р | ||||||
| А | А | В | К | О | П | Р | У |
| Р | У | ||||||
| А | А | В | К | О | П | Р | У |
Рисунок 3 Пузырьковая сортировка
Дата добавления: 2022-02-05; просмотров: 543;











