Алгоритм на псевдокоде
Метод прямого включения
DO (i: = 2, 3, … n)
t: = ai, j: =i-1
DO (j > 0 и t < aj)
aj+1:= aj
j: = j-1
OD
aj+1:= t
OD
Для метода прямого включения справедливы следующие оценки величин М и С.
Cmin £ Ссред £ Cmax, где Cmin = n-1, Cmax = 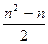 ,
,
Мmin £ Мсред £ Мmax, где Мmin = 2(n-1), Mmax = 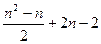 .
.
Минимальные и максимальные значения величин С и М достигаются на прямо отсортированном и обратно отсортированном массивах соответственно. Таким образом, средняя трудоемкость этого метода имеет квадратичный порядок, т.е. С = О(n2) М = О(n2), при n®¥.
Метод прямого включения устойчивый.
3.2 Метод Шелла
На базе метода прямого включения разработан алгоритм, обеспечивающий значительную производительность сортировки. Мы заметили, что в методе прямого включения, чем больше упорядочен массив, тем меньше операций требуется для его сортировки. При сортировке уже упорядоченного массива трудоемкость имеет линейный порядок. Поэтому имеет смысл попытаться предварительно несколько улучшить порядок элементов в массиве, а затем отсортировать массив методом прямого включения.
Предварительное упорядочивание будем проводить с помощью k – сортировок. Суть k – сортировки заключается в следующем. Массив разбивается на последовательности с шагом k
ai, ak+i, a2k+i, …,a[n/k]k+i, i = 1, 2,…,k
и сортировка происходит только внутри этих последовательностей.
Обозначим через H последовательность из m возрастающих шагов
H=(h1, h2, … hm), где h1=1, h1 < h2 < h3 < … < hm
Метод Шелла состоит в последовательном проведении hi-сортировки, i=m, m-1,…, 1, причем h1=1 гарантирует, что массив будет полностью отсортирован, поскольку 1-сортировка является методом прямого включения.
Пример.Отсортировать слово методом Шелла. Последовательность шагов выберем следующим образом h1=1, h2=2.
2-сортировка
| К | У | Р | А | П | О | В | А |
| |||||||
| К | У | Р | А | П | О | В | А |
| К | А | Р | У | П | О | В | А |
| К | А | П | У | Р | О | В | А |
| К | А | П | О | Р | У | В | А |
| В | А | К | О | П | У | Р | А |
| В | А | К | А | П | О | Р | У |
1-сортировка
| В | А | К | А | П | О | Р | У |
| А | В | К | А | П | О | Р | У |
| А | В | К | А | П | О | Р | У |
| А | А | В | К | П | О | Р | У |
| А | А | В | К | П | О | Р | У |
| А | А | В | К | О | П | Р | У |
| А | А | В | К | О | П | Р | У |
Рисунок 6 Метод Шелла
Дата добавления: 2022-02-05; просмотров: 537;











