Алгоритм на псевдокоде

Сортировка методом Шелла

DO (k=h_m, h_m-1, … 1)

DO (i=k+1, k+2, … n)

t: = a_i, j: =i-k

DO (j>0 и t < a_j)

a_j+k: = a_j

j: = j-k

OD

a_j+k: = t

OD

OD

Эффективность метода зависит от выбора значений шагов. Последовательность значений шагов, которая дает наилучшую трудоемкость, пока неизвестна, метод продолжает исследоваться, но существует и часто используется следующая последовательность шагов, предложенная Кнутом.

h₁=1, h_i=2h_i-1+1, i=2,… m, m=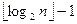

При такой последовательности шагов средний порядок трудоёмкости O(n^1.2), n → ∞. Таким образом, метод Шелла существенно быстрее методов с квадратичной трудоемкостью. Метод Шелла не устойчив.

3.3 Варианты заданий

1. Разработать процедуру сортировки массива целых чисел методом прямого включения (язык программирования Паскаль или Си). Правильность сортировки проверить путем подсчета контрольной суммы и числа серий в массиве. Предусмотреть подсчет количества пересылок и сравнений (М и С), сравнить их с теоретическими оценками.

2. Разработать процедуру сортировки массива целых чисел методом Шелла (язык программирования Паскаль или Си). Правильность сортировки проверить путем подсчета контрольной суммы и числа серий в массиве. Предусмотреть подсчет количества пересылок и сравнений (М и С), сравнить их с теоретическими оценками.

3.Сравнить метод прямого включения и метод Шелла по количеству сравнений и пересылок для различных типов массивов. Разработать процедуру построения графика зависимости величин М и С от размера массива.

4. Сравнить метод прямого включения и метод Шелла с ранее расмотренными методами сортировки по количеству сравнений и пересылок для различных типов массивов. Разработать процедуру построения графика зависимости величин М и С от размера массива

5. Экспериментально определить подходящую последовательность шагов для метода Шелла.

6. Опытным путем определить константы в выражениях оценки для количества сравнений и пересылок в методе Шелла.

4. Быстрые методы сортировки массивов

4.1 Пирамидальная сортировка

Пирамидальная сортировка основана на алгоритме построения пирамиды. Последовательность a_i, a_i+1,…,a_k называется (i,k)-пирамидой, если неравенство

a_j≤min(a_2j, а_2j+1) (*)

выполняется для каждого j, j=i,…,k для которого хотя бы один из элементов a_2j, a_2j+1 существует.

Например, массив А является пирамидой, а массив В ¾ не является.

А=(а₂ , а₃ , а₄ , а₅ , а₆ а₇ , а₈ )=(3, 2, 6, 4, 5, 7)

В=(b₁, b₂, b₃, b₄, b₅, b₆, b₇)=(3, 2, 6, 4, 5, 7)

Свойства пирамиды

1. Если последовательность a_i, a_i+1,…,а_k-1, a_k является (i, k)-пирамидой, то последовательность a_i+1,…,a_k-1, полученная усечением элементов с обоих концов последовательности, является (i+1, k-1)пирамидой.

2. Если последовательность a₁…a_n – (1, n)-пирамида, то а₁ – минимальный элемент последовательности.

3. Если a₁, a₂…,a_n/2,a_n/2+1,…a_n-произвольная последовательность, то последовательность a_n/2+1,…,a_n является (n/2+1, n)-пирамидой.

Процесс построения пирамиды выглядит следующим образом. Дана последовательность a_s+1,…,a_k, которая является (s+1, k)-пирамидой. Добавим новый элемент х и поставим его на s-тую позицию в последовательности, т.е. пирамида всегда будет расширяться влево. Если выполняется (*), то полученная последовательность – (s, k)-пирамида. Иначе найдутся элементы a_2s+1,a_2s такие, что либо a_2s < a_s либо a_2s+1 < a_s.

Пусть имеет место первый случай, второй случай рассматривается аналогично. Поменяем местами элементы a_s и a_2s. В результате получим новую последовательность a_s^’,a_s+1,…, a_2s^’,…, a_k. Повторяем все действия для элемента a_2s^’ и т.д. пока не получим (s, k)-пирамиду.

Пример.Добавим в (2, 8)-пирамиду новый элемент х=6.

Условные обозначения: Х новый элемент

Х сравнение с включаемым элементом

обмен элементов

								пирамида
6	3	2
					4	5
								пирамида

Рисунок 7 Добавление в пирамиду нового элемента