Основная теорема кодирования для канала связи без шума (теорема 3)

Теорема 3.

Формулировка. При заданной энтропии H источника и объеме m вторичного алфавита существует префиксный код с минимальной средней длиной n_{ср min} кодовых слов, отвечающей следующему неравенству:

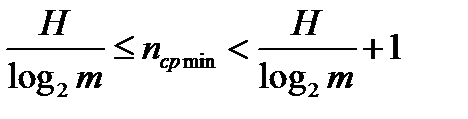. (3.3)

Доказательство

Докажем сначала левую часть неравенства (3.3), для чего перепишем его в виде: .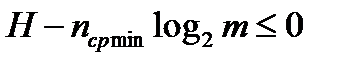

Далее выполним преобразования:

.

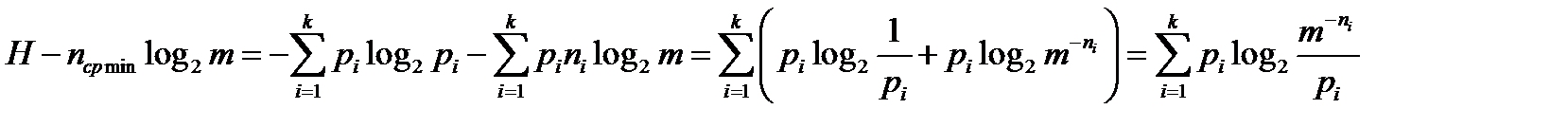Если разложить логарифм log₂x в ряд Тэйлора (степенной ряд) и взять первые 2 члена этого ряда, получим следующее неравенство: log₂x <= (x-1) log₂e .

Используя это неравенство, продолжим преобразование нашего выражения:

.

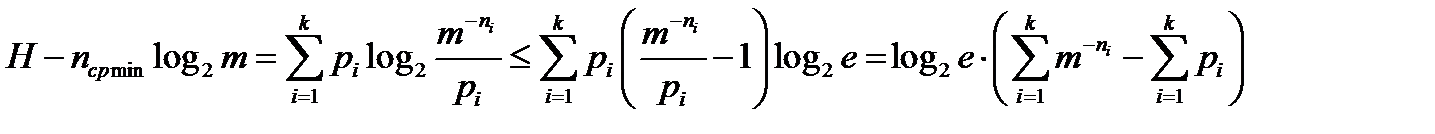Поскольку n_i – длины кодовых слов префиксного кода, согласно неравенству Крафта (3.1), первая сумма в скобках 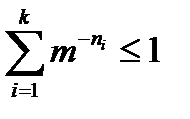. Вторая сумма = 1, т.к. является полной суммой вероятностей. Следовательно, уменьшаемое в скобках меньше вычитаемого и сама разность отрицательна. Логарифм log₂e >0, следовательно, само выражение отрицательно: 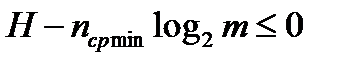. Отсюда следует, что 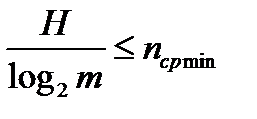и, таким образом, левая часть неравенства (3.3) доказана.

Докажем теперь правую часть неравенства (3.3).

Заметим, что при 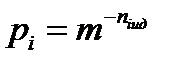логарифм в правой части равенства 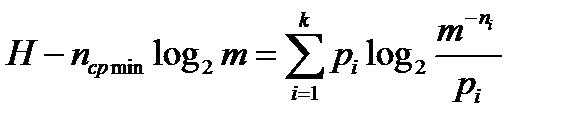становится равным 0. Тогда неравенство превращается в равенство 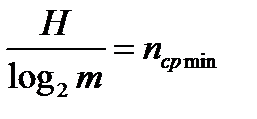. Достичь этого можно было бы, если бы идеальные длины n_iид кодовых слов находились из выражения 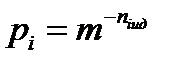(n_iид=-log_mp_i), однако в общем случае они должны бы тогда быть дробными числами, что невозможно. Эти длины должны быть целыми числами и, кроме того, их значения должны соответствовать неравенству Крафта (напомним, что теорема доказывается для префиксного кода): 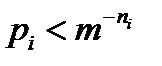. Значит, в качестве реальных длин кодовых слов можно выбирать ближайшее большее целое число. Максимальное же отличие реальной и идеальной длины при этом может приближаться к 1. Если предположить наихудший случай, когда все длины отличаются от идеальной на 1, то

.

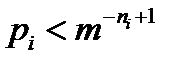Отсюда, логарифмируя левую и правую части неравенства, находим: .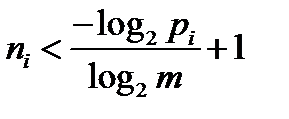

Умножая правую и левую части этого неравенства на p_i и суммируя результаты по всем i, получаем правую часть неравенства (3.3).

Таким образом, теорема 3 о минимальной средней длине кодового слова (основная теорема кодирования для канала без шума) доказана.