Теорема о минимальной средней длине кодового слова при поблочном кодировании (теорема 4)
Рассмотрим теперь случай кодирования не отдельных букв источника, а последовательностей из L букв.
Теорема 4.
Формулировка. Для данного дискретного источника без памяти (с независимыми буквами) и энтропией H и объемом вторичного алфавита m при кодировании блоками по L букв существует префиксный код со средней длиной кодового слова, отвечающей неравенству:
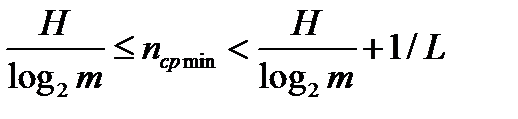 .
.
Доказательство.
Последовательность из L букв можно рассматривать как новую супербукву. Тогда можно использовать теорему 3, согласно которой минимальная средняя длина кодового слова для такого сообщения ограничивается неравенством:
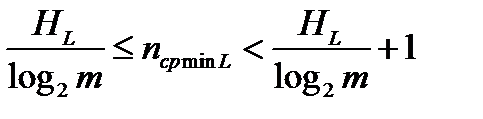 .
.
Так как отдельные буквы предполагаются независимыми, то энтропия последовательности L букв 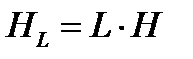 . Кроме того, средняя длина кода для последовательности L букв
. Кроме того, средняя длина кода для последовательности L букв 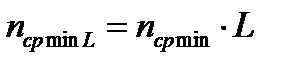 , тогда
, тогда
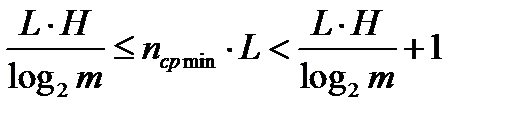 .
.
После деления всех частей неравенства на L получаем окончательный результат: 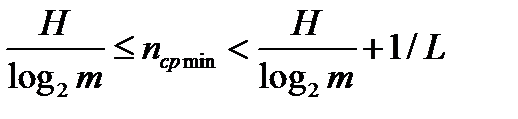 .
.
Из теоремы 4 следует, что если кодировать блоками, то, увеличивая размер блоков L, можно сколь угодно приблизиться к нижней границе средней длины кодового слова, т.е. 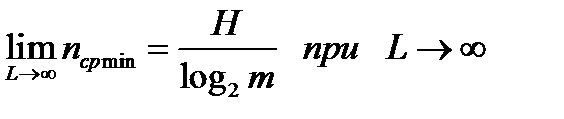 .
.
Дата добавления: 2021-04-21; просмотров: 489;











