Выбор периода дискретизации (квантования по времени) по критерию наибольшего отклонения

В результате квантования по времени функции x(t) получается ряд значений x(t₁), x(t₂), … квантуемой величины x(t) в дискретные моменты времени t₁, t₂, … Период квантования 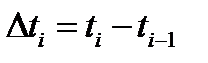может быть постоянным, когда 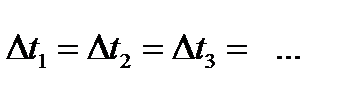, и переменным, когда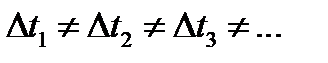

Если функция x(t) имеет ограниченный максимальной частотой 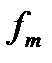спектр, время ее воспроизведения и сложность воспроизводящего устройства не имеют существенного значения, хорошего воспроизведения можно достичь при помощи ряда Котельникова. Необходимая частота дискретизации при этом, как ранее было показано, равна удвоенной максимальной частоте, а период дискретизации 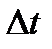, следовательно, находится по формуле .

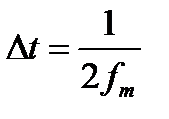Чаще, однако, одно или несколько из вышеуказанных условий не выполняется и тогда используют другие принципы выбора периода дискретизации и способы воспроизведения. Период дискретизации при этом, как правило, уменьшается в 5 – 10 раз.

При воспроизведении исходной функции широко используют хорошо проработанные в математике методы интерполяции, приближения и экстраполяции. При интерполяции по уже полученным отсчетам восстанавливаются прошлые значения функции, причем, чем больше этих отсчетов используется, тем точнее восстановление.

Методы экстраполяции позволяют предсказать будущие значения функции (прогнозировать), что для некоторых задач чрезвычайно важно (вспомним, например, прогноз погоды). И здесь, чем больше отсчетов используется для экстраполяции (предсказания), тем точнее предсказания выше.