Элементы обобщенной спектральной теории сигналов

Обобщенная спектральная теория сигналов объединяет методы математического описания сигналов и помех. Эти методы позволяют обеспечить требуемую избыточность сигналов с целью уменьшения влияния помех, облегчает анализ и синтез систем передачи информации и т.п.

Сигналы в обобщенной спектральной теории описываются в виде:

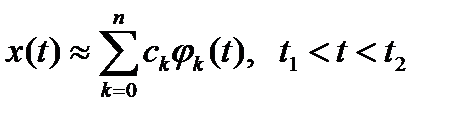, (2.1)

где x(t) – описываемый сигнал;

с_k – коэффициенты разложения сигнала x(t) в ряд по системе функций 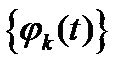( фигурные скобки обозначают множество);

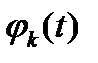− заранее известные функции, входящие в систему (множество) 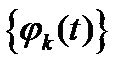; система в данном случае состоит из n+1 членов.

О записи (2.1) еще говорят, что она описывает разложение сигнала x(t) в ряд по системе функций 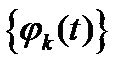. Функции, входящие в систему 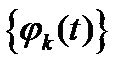, называют базисными, а саму систему 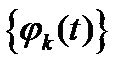− базисом разложения.

Если функции 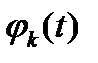отвечают условию:

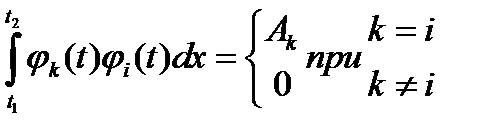, (2.2)

то такие функции называются ортогональными. Это очень удобное свойство. Поэтому для разложений (2.1) чаще всего используют именно системы ортогональных функций.

Кроме того, выбирают функции, отвечающие еще одному условию:

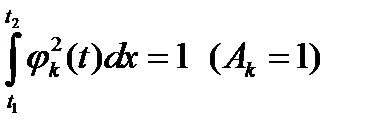. (2.3)

Функции, отвечающие условию (2.3) называются нормированными, а условиям (2.2) и (2.3) одновременно – ортонормированными.

Разложение (2.1), в котором используются ортогональные функции, называется ортогональным, а если используются ортонормированные функции, то ряд называется ортонормальным. Ряд Фурье является ортогональным, но не ортонормальным.

Ошибка разложения находится по формуле:

.

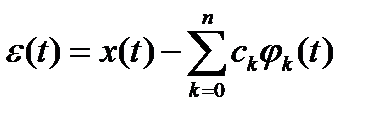В качестве критерия ошибки будем использовать среднеквадратическую погрешность, которая в данном случае будет записываться в виде:

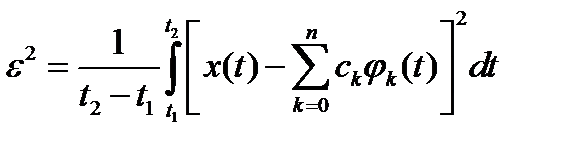. (4)

Найдем выражение для коэффициентов c_k, минимизирующих среднеквадратическую погрешность ортогонального разложения. На коэффициенты при этом никаких условий не накладывается. Для минимизации следует решить систему уравнений при k=0, 1,…, n. Если при этом окажется, что 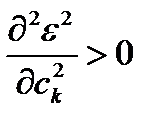, то найденное решение минимизирует .

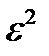Для решения задачи представим 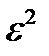в виде:

.

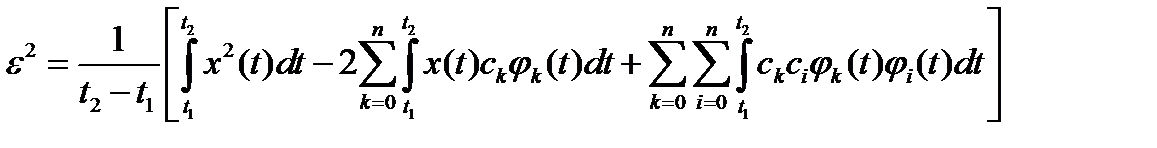Третье слагаемое с учетом ортогональности (2.2) равно: .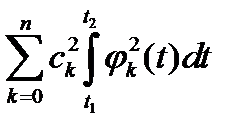

В результате: .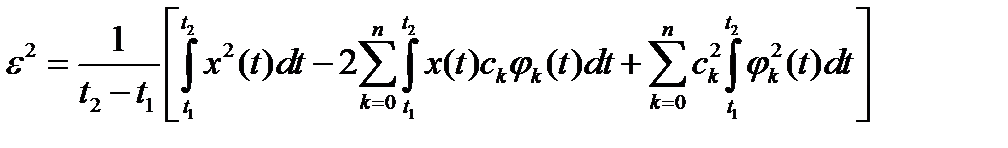

Находим производную:

.

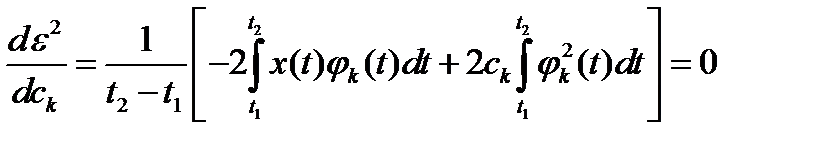Если предложить нормированность функций 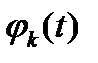, то второе слагаемое равно 2с_k . В результате легко найти c_k:

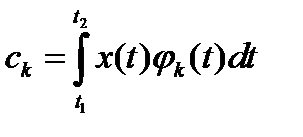. (2.5)

Несложно заметить, что вторая производная положительна. Таким образом, для того, чтобы среднеквадратическая погрешность ортонормального разложения была минимальна, коэффициенты разложения должны вычисляться по формуле (2.5).

Существует бесконечно много базисных систем. Легко показать, что при одном и том же числе n членов разложения в общем случае среднеквадратическая погрешность при их применении будет различна.

Можно поэтому подыскать такую базисную систему, при которой погрешность будет наименьшей.

Примером такого разложения является разложение в ряд Котельникова.