Оценка максимального значения ошибки при получении воспроизводящей функции на основе полинома Лагранжа

Найдем погрешность интерполяции. Представим ее виде:

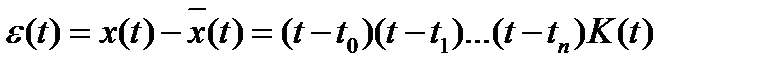, (2.16)

где K(t) – вспомогательная функция, которую надо найти.

Для произвольного t* имеем:

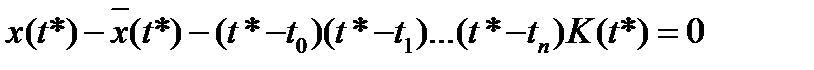(2.17)

Введем в рассмотрение еще одну функцию

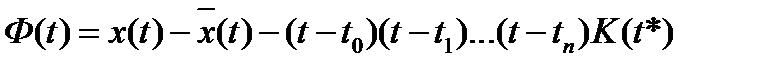(2.18)

Продиффенцируем ее n+1 раз по t.

Так как 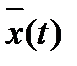- полином n-ой степени, то .

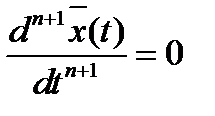K(t*) –константа, значит

.

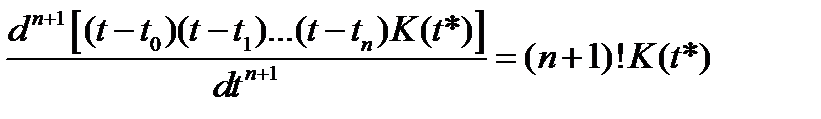Следовательно 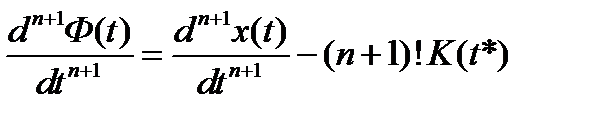. (2.19)

Функция Ф(t) пересекает ось t как минимум n+2 раз (при значениях аргумента t в точках t₁, t₂, …, t_n и t* − см. (2.17), (2.18), см. рис. 2.6).

Это значит, что первая производная имеет хотя бы n+1 нулей (по одному на нулю на каждом интервале), вторая производная – n нулей и т.д. n+1-я производная должна иметь хотя бы одно нулевое значение при некотором .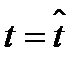

Рис. 2.6. Точки пересечения оси Ф функцией Ф(t).

Отсюда, учитывая (2.19), в этой точке

.

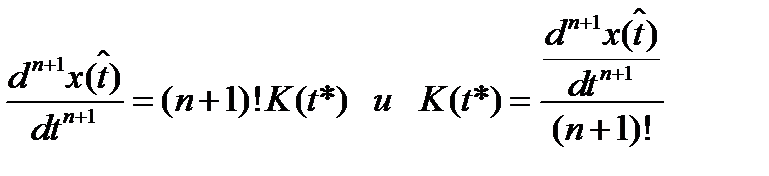Подставив эту формулу в формулу ошибки воспроизведения (2.16), получим:

.

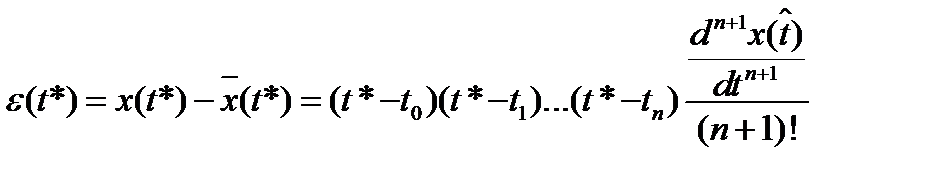Так как t* произвольно, его можно заменить на t:

.

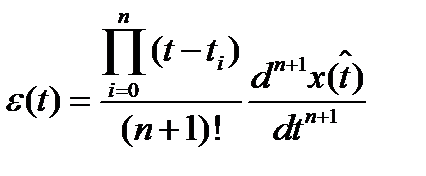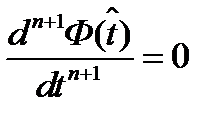выбиралось из условия . На практике найти сложно. Если вместо 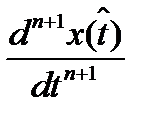подставить 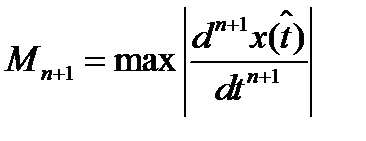и вместо подставить 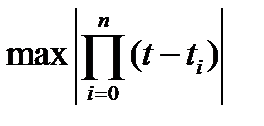, то получаем оценку абсолютной величины ошибки сверху:

.

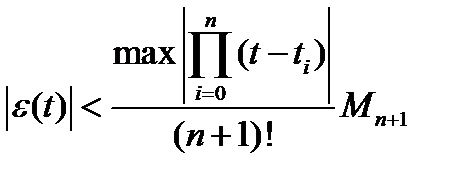Таким образом, для определения наибольшего отклонения воспроизводящей функции, представленной полиномом Лагранжа, от исходной необходимо знать максимальное по абсолютной величине значение производной исходной функции.

Приступим теперь к решению обратной задачи – по заданному значению максимальной погрешности 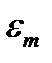, порядку n полинома Лагранжа и максимальному значению производной M_n находить максимально возможный шаг равномерной дискретизации.