Разложение в ряд Котельникова (Теорема Котельникова)

Описанный здесь результат Котельниковым был получен 1933 г., но ранее подобные результаты были получены в 1915 г. Виттакером и в 1928 г. Найквистом.

Котельников доказал, что, если некоторый сигнал x(t) имеет ограниченный сверху частотой f_m спектр, то его можно проквантовать по времени с периодом 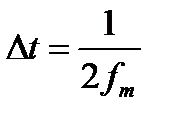и затем с абсолютной точность восстановить по формуле:

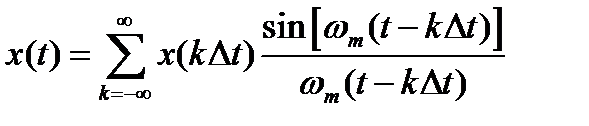(2.6)

Ряд (2.6) называется рядом Котельникова, а вышеуказанное утверждение – теоремой Котельникова.

По определению сигнал x(t) и его спектр S(jω) находятся в следующих отношениях:

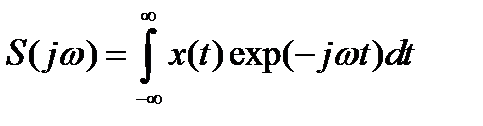; (2.7)

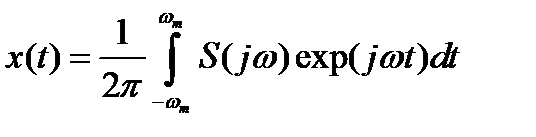. (2.8)

Формулы (2.7) и (2.8) образуют пару преобразований Фурье (прямое и обратное. Ограниченный интервал интегрирования в (2.8) – следствие ограниченности спектра, поскольку 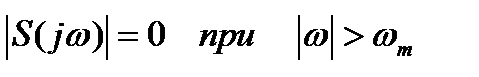. Здесь ω – круговая частота, а .

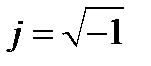Образуем новый спектр S_п(jω) путем периодического (с периодом 2ω_m) продолжения спектра S(jω) вдоль оси ω.

Тогда его, как периодическую функцию можно разложить в ряд Фурье:

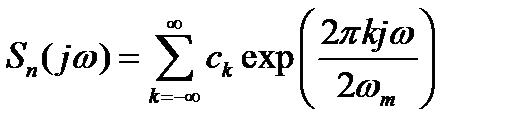, (2.9)

где 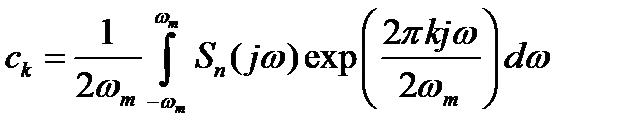. (2.10)

В формулах (2.8) и (2.10) можно подставлять как S(jω), так и S_п(jω), так как на участке интегрирования они равны.

Сравним (2.8) и (2.10). Интегралы совпадают, если в (2.8) положить:

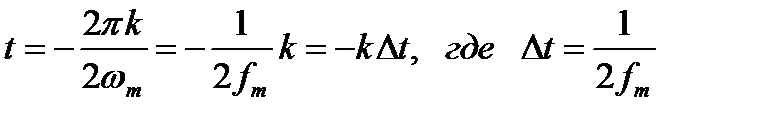
Домножим, кроме того, правую и левую части (2.8) на 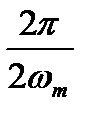. Тогда правая часть (2.8) совпадет с левой частью (2.10). Следовательно, можно приравнять и левые части:

.

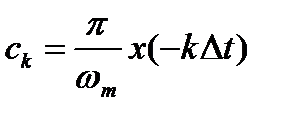Подставим выражение для с_k в (2.9):

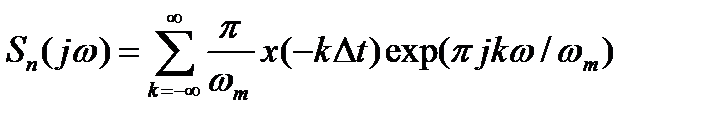. (2.11)

Подставим (2.11) в (2.8), так как S(jω) = S_п(jω) при –ω_m<=ω<=ω_m :

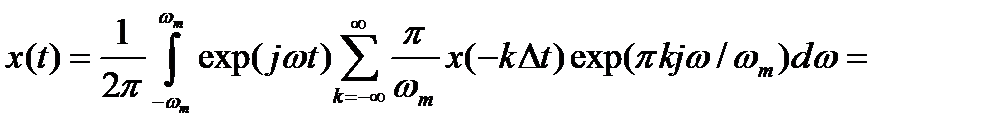
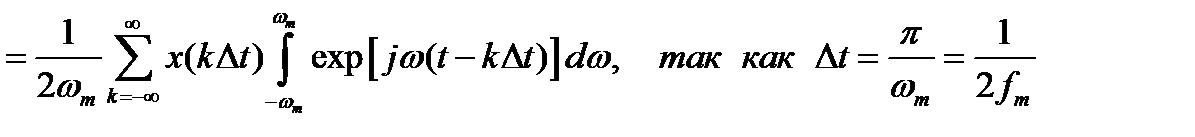(2.12)

Возьмем интеграл .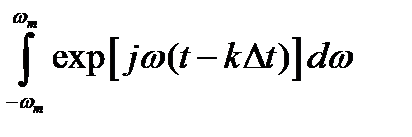

Введем обозначение z=t-kΔt, тогда определенный интеграл берется:

.

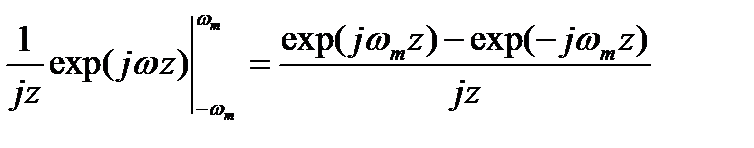Учитывая, что 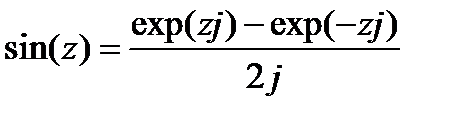получаем:

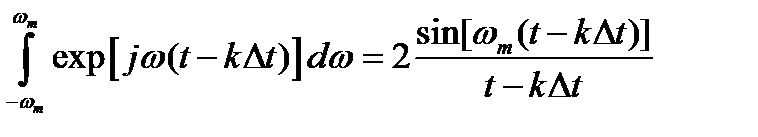. (2.13)

Подставим (2.13) в (2.12):

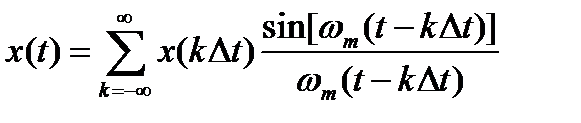, что и требовалось доказать.

Обозначим .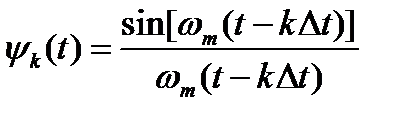

Функция 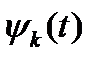называется функцией отсчетов.

Тогда формула восстановления принимает вид:

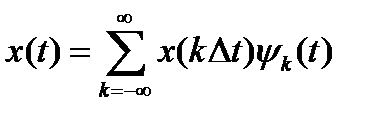
На рис. 2.4 изображена форма двух разных функций отсчетов:

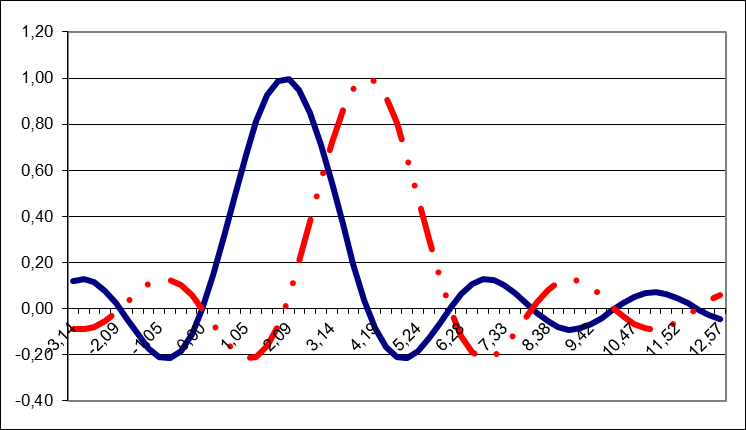
Рис. 2.4. Графики функций отсчетов.