О практическом использовании теоремы Котельникова

Возможную схему квантования-передачи-восстановления непрерывного сигнала можно представить в виде, изображенном на рис. 2.5.

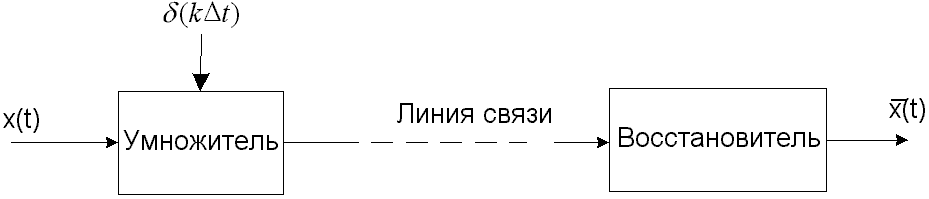
Рис. 2.5. Возможная схема квантования-передачи-восстановления непрерывного сигнала.

Технически восстановитель исходной функции может быть реализован при помощи электронного устройства, называемого идеальным фильтром нижних частот. Этот фильтр отличается тем, что на импульсное воздействие, описываемое так называемой дельта-функцией 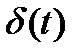, реагирует сигналом h(t) в виде функции отсчетов .

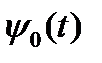Дельта-функция задается формулой:

.

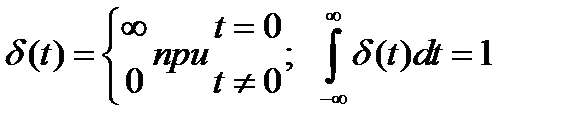Реакция h(t) идеального фильтра нижних частот на входное воздействие в виде дельта-импульса равна:

.

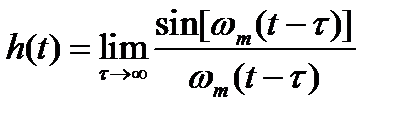Фильтр нижних частот, как и широкий класс электрических схем, является линейным устройством. Эти устройства отличаются тем, что их реакция на сумму воздействий равна сумме реакций на каждое воздействие в отдельности. Таким образом, если на вход такого устройства к примеру подать последовательность импульсов, его реакция будет равна сумме реакций на каждый импульс в отдельности.

Так реализуется получение суммы в формуле (6). Но результат все же отличается:

.

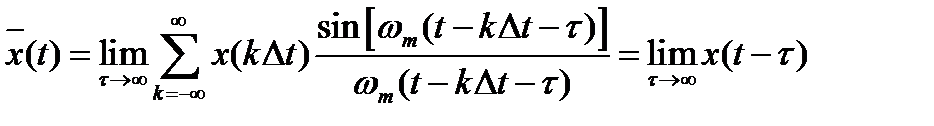Восстановленная функция оказывается смещенной по оси x на бесконечно большую величину.

Вторая принципиальная трудность практического использования теоремы Котельникова заключается в том, что все реальные сигналы конечны во времени. Математически доказывается, что в этом случае их спектр не ограничен максимальной частотой. Доказано, что ограниченный спектр могут иметь только сигналы бесконечно большой длительности.

По этой причине f_m приходится определять приближенно, руководствуясь, в зависимости от конкретных условий, различными рекомендациями.

Можно, например, f_m определить по доле энергии сигнала, сосредоточенной в диапазоне частот от 0 до f_m :

.

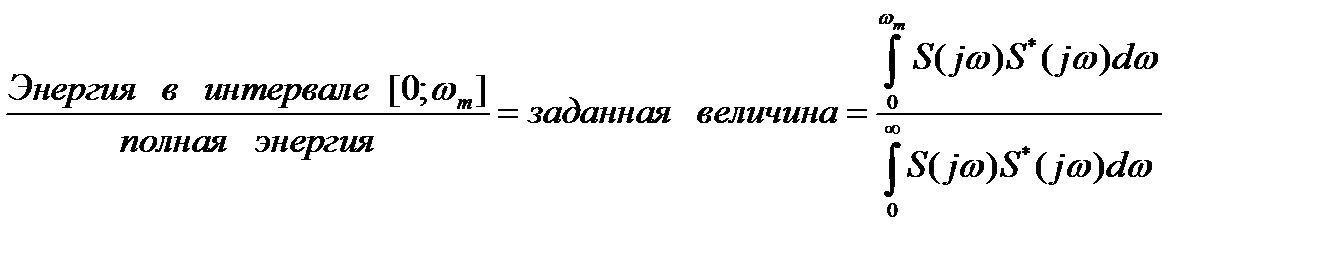Некоторые рекомендации позволяют сразу определить период квантования. Это, например, рекомендация, предложенная Железновым в 1960 г., согласно которой период дискретизации предлагается выбирать равным так называемому интервалу корреляции:

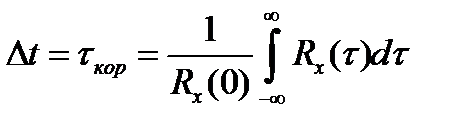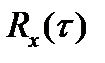, где - корреляционная функция.

Корреляционная функция связана со спектром следующей зависимостью:

.

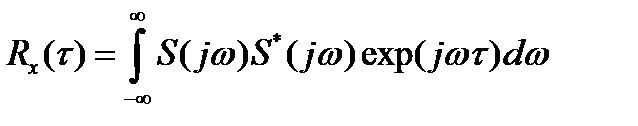Этот способ согласуется с результатом, полученным Котельниковым и, если спектр ограничен, дает полностью совпадающие результаты. Это означает, что отсчеты по Котельникову представляют собой ближайшие некоррелированные (независимые) значения квантуемого сигнала (если бы отсчеты брались с меньшим периодом, они были бы зависимы, т.е. несли бы частично совпадающую информацию, что излишне нагружало бы каналы связи).

В заключение заметим, что, хотя теорема Котельникова и базируется на идеализированной модели сигналов, она имеет большую практическую и теоретическую ценность.