Выбор интервала дискретизации по критерию среднеквадратического отклонения

Рассмотрим случай дискретизации случайного стационарного эргодического процесса x(t) с известной корреляционной функцией 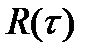. Восстанавливать будем при помощи полиномов Лагранжа. Наиболее часто используются полиномы нулевого и первого порядка.

Начнем с полинома нулевого порядка.

Ошибка, как известно, вычисляется по формуле: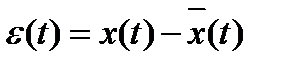

Дисперсия 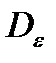ошибки в случае стационарных эргодических процессов может быть вычислена по формуле:

,

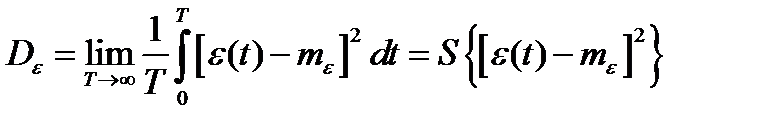где 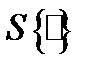− оператор усреднения по времени, 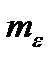− среднее значение (математическое ожидание) ошибки.

Найдем :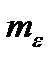

,

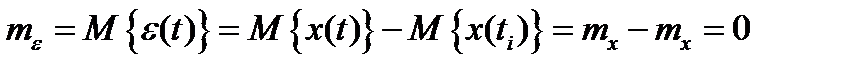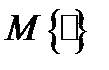− оператор математического ожидания.

Значит .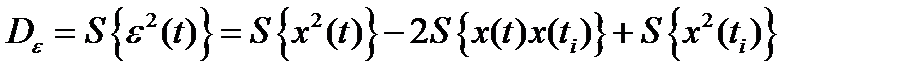

Найдем каждое из этих средних.

1) ;

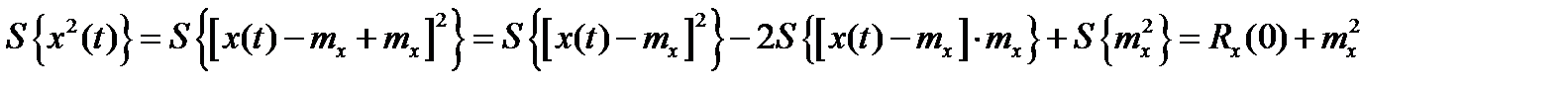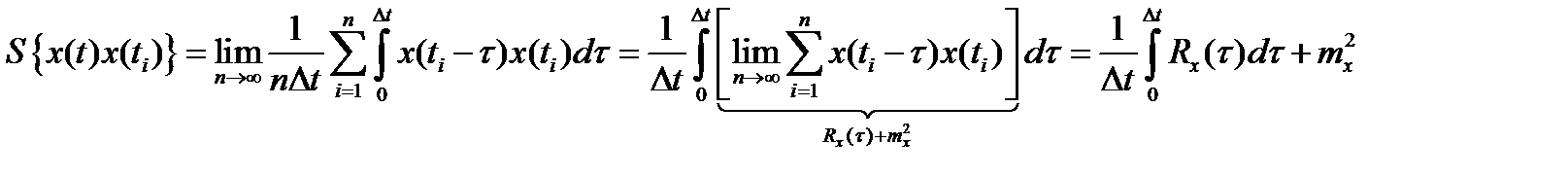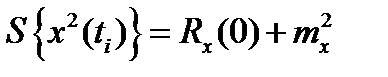2) по аналогичной причине;

3) .

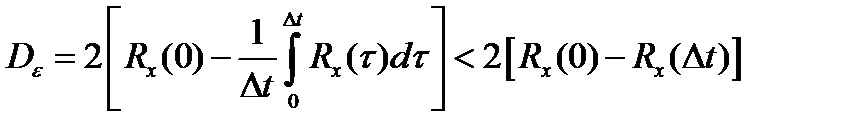
В итоге:

Отсюда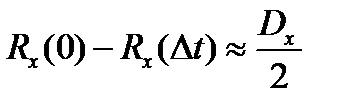

Используя эту формулу, шаг дискретизации 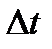можно найти графически так, как показано на рис. 2.12.

Рис. 2.12. Порядок графического определения шага дискретизации, если использовать критерий среднеквадратического отклонения.

В заключение отметим, что найдены также выражения для дисперсии ошибки и при восстановлении с помощью полиномов более высоких, чем нулевой, порядков.