АДАПТИВНОЕ И ИНТЕЛЛЕКТУАЛЬНОЕ УПРАВЛЕНИЕ
| 7.1 Общие сведения об адаптации и интеллектуальности в САУ |
Периодизация развития теории управления определяется поставленными целями. По рассматриваемому вопросу неоспорим и общепризнан вклад Я.З. Цыпкина, который считал, что в развитии теории управления следует выделить три периода: детерминизма, стохастичности и адаптивности. В настоящее время мы являемся свидетелями становления нового, четвертого периода развития теории управления: периода интеллектуальности.
В период детерминизма уравнения, описывающие состояния ОУ, и внешние воздействия (задающие и возмущающие) предполагались известными. Полная определенность в постановке задач анализа и синтеза САУ позволяла широко использовать классический аналитический аппарат для решения различных проблем теории управления. Особенно это относится к линейным САУ, рассмотренным в разделах 2 и 3. Для линейных систем принцип суперпозиции существенно облегчал решение задач исследования САУ и создавал видимость отсутствия принципиальных затруднений. Затруднения возникли при необходимости учета нелинейностей (см. разделы 4 - 6), но и здесь, несмотря на отсутствие общих регулярных методов, удается при наличии полной информации об ОУ и внешних воздействиях успешно решать задачи анализа и синтеза САУ.
Для периода стохастичности характерен учет более реальных условий работы САУ. Было установлено, что внешние воздействия, задающие, а особенно возмущающие, непрерывно изменяются во времени и заранее не могут быть определены однозначно. В некоторых случаях это относится и к коэффициентам уравнений ОУ. Поэтому возникла необходимость в привлечении иных подходов, учитывающих вероятностный характер внешних воздействий и уравнений. Эти подходы основаны на знании статистических характеристик случайных функций и также используют аналитические методы.
Характерная особенность названных двух периодов развития теории управления состоит в том, что она применима к системам с достаточной априорной информацией, т.е. уравнения ОУ и внешние воздействия либо их статистические характеристики предполагаются известными.
В период адаптивности, наступившей в 60-е годы, учитываются самые разнообразные условия работы современных сложных САУ, при этом уравнения ОУ и внешние воздействия (либо их статистические характеристики) могут не только быть неизвестными, но по различным причинам отсутствует возможность заранее определить их экспериментальным путем. Иначе говоря, исследователь сталкивается с большей или меньшей начальной (априорной) неопределенностью. Возможность управления объектами при неполной и даже весьма малой априорной информации основана на применении адаптации и обучения САУ, которые уменьшают первоначальную неопределенность на основе использования информации, получаемой в течение процесса управления. Таким образом, под адаптацией понимают процесс изменения параметров и структуры системы, а возможно, и управляющих воздействий на основе текущей информации с целью достижения определенного, обычно оптимального, состояния системы при начальной неопределенности и изменяющихся условиях работы.
В середине 90-х годов начинается четвертый период развития теории управления, который по аналогии с названиями предыдущих удобно назвать периодом интеллектуальности. Становление нового научного направления в теории управления - теории интеллектуального управления - отмечают многие ученые (В.Н. Захаров, А.А. Ерофеев и др.). Это направление появилось на стыке ТАУ и теории искусственного интеллекта. В теории интеллектуального управления пока нет устоявшейся терминологии и однозначного понимания существа протекающих в интеллектуальных системах управления (ИСУ) процессов, однако характерным отличием ИСУ от предшествующих типов САУ, в том числе адаптивных САУ, является взаимодействие с внешней средой, которая для ИСУ является не только источником возмущений, но и источником информации. ИСУ - информационно связанные с реальным внешним миром системы, которые "живут" в естественном внешнем мире и перерабатывают информацию из этого мира.
Вместе с Я.З. Цыпкиным подчеркнем, что периоды детерминизма, стохастичности, адаптивности и интеллектуальности не сменяют друг друга подобно кадрам в кино. Каждый из них зарождается в недрах предшествующих периодов, и их проблематика существует в настоящее время.
На начальной стадии каждого из периодов в основном решалась задача анализа систем и выяснения их свойств. Затем появились задачи синтеза систем, удовлетворяющих определенным требованиям. Вполне естественно, что чаще всего задача синтеза САУ ставилась и решалась на основе оптимизационного подхода в силу его универсальности.
Несмотря на новизну проблем адаптации и интеллектуализации САУ число научных работ, посвященных этим проблемам, чрезвычайно велико, достаточно разнообразны также методы анализа и синтеза адаптивных и интеллектуальных САУ. Однако при рассмотрении проблем адаптации и обучения в САУ для учебных целей следует отдать предпочтение подходу Я.З.Цыпкина, в котором разнообразные задачи адаптации решаются на основе вероятностных итеративных методов.
В качестве критерия оптимальности (показателя качества) предлагается рассматривать условное математическое ожидание
J(c) = My{F(y,c)} = F(y,c)p(y)dy, (7.1)
где F(y,c) - функционал вектора c = (c1, ..., cn), зависящий также от вектора случайных последовательностей или процессов у = (у1, ..., уm), плотность распределения которого равна р(у); Y - пространство векторов у (условимся, что здесь и далее все векторы представляются столбцовыми матрицами).
Векторы у и с, входящие в функционал критерия оптимальности, стеснены ограничениями вида
My{hv(y,c)} = 0 (v = l, 2, ..., M1) (7.2)
или My{hv(y,c)} ≤ 0 (v = l, 2, ..., M2). (7.3)
Если функции распределения для случайных процессов у известны и можно определить в явной форме критерии качества J(c), то стохастическая задача оптимизации (7.1) принципиально не отличается от детерминированной, рассмотренной в разделе 6.
Существенно иная ситуация возникает, когда функция распределения заранее неизвестна. Здесь уже обычный подход теряет силу и необходим иной, адаптивный подход. Адаптивный подход может быть применен и в тех случаях, когда применение обычного хотя и возможно, но сопряжено с большой работой по предварительному определению функций распределения.
Итак, решение проблемы оптимальности сводится к определению такого вектора с*, который, удовлетворяя ограничениям (7.2), (7.3), доставлял бы функционалу (7.1) экстремальное значение. Для решения задачи оптимизации применяются самые разнообразные методы, которые можно разделить на аналитические и алгоритмические.
Аналитические методы на первый взгляд представляются наиболее привлекательными, т.к. они приводят к явному формульному решению задачи. Но эти методы пригодны для решения относительно простых задач.
Алгоритмические методы не дают явного формульного решения задачи, а лишь указывают алгоритм, т.е. последовательность действий, операций, осуществление которых приводит к искомому решению
| 7.1.1 Условия оптимальности |
Рассмотрим вначале случай достаточной априорной информации, т.е. функционал J(с) известен в явной форме, известны также ограничения. Если функционал J(c) допускает дифференцирование, то он достигает экстремума (максимума или минимума) только при таких значениях c = (c1, ..., cN), для которых N частных производных 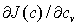 (v = 1, 2, ..., N) одновременно обращаются в нуль, или, иначе говоря, для которых градиент функционала
(v = 1, 2, ..., N) одновременно обращаются в нуль, или, иначе говоря, для которых градиент функционала 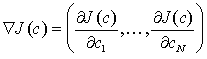 обращается в нуль. Векторы с, удовлетворяющие условию
обращается в нуль. Векторы с, удовлетворяющие условию
∇J(с) = 0 , (7.4)
называются стационарными или особыми. Не все стационарные векторы оптимальны, т.е. соответствуют нужному экстремуму функционала. Поэтому (7.4) является лишь необходимым условием оптимальности.
Можно было бы выписать и достаточные условия экстремума, однако, исходя непосредственно из условий задачи, удается определить, чему соответствует оптимальный вектор - минимуму или максимуму. Условие оптимальности (7.4) выделяет лишь локальные экстремумы, и если их много, то задача нахождения глобального экстремума становится очень сложной. Ограничимся случаем, когда оптимальное значение вектора единственно и соответствует минимуму J(с).
| 7.1.2 Итеративные алгоритмы оптимизации |
Основная идея решения уравнения (7.4) состоит в поиске оптимального вектора с помощью последовательных приближений или итераций:
с[n] = с[n-1] - γ[n]∇J(c[n-1]) , (75)
где n = 0, 1, 2,... - дискретное время (номер итерации).
Значение γ[n] определяет величину очередной итерации. При выполнении соответствующих условий сходимости для любого начального выбора с[0] оказывается, что
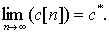
Итак, соотношение (7.5) определяет последовательность действий, которые нужно осуществить, чтобы определить оптимальный вектор с*. Используя (5.28), алгоритм оптимизации (7.5) можно переписать в виде
∆c[n-1] = -γ[n]∇J(c[n-1]). (7.6)
Алгоритмы (7.5) и (7.6) - дискретные алгоритмы оптимизации.Предельным переходом из них можно получить непрерывный алгоритм оптимизации
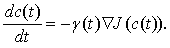 (7.7)
(7.7)
| 7.1.3 Вероятностные итеративные алгоритмы |
Пусть критерий (7.1) в явной форме неизвестен. Это значит, что плотность распределения р(х) неизвестна, а известны лишь реализации F(y,c), которые зависят от стационарных последовательностей или процессов у и вектора с.
Очевидно, единственно возможный способ определения связан с наблюдением реализаций и их обработкой. Ясно, что регулярные итеративные алгоритмы (7.5) - (7.7) здесь непригодны, но для решения проблемы оптимальности в условиях недостаточной априорной информации естественно использовать идейную сторону итеративных методов.
Для пояснения идеи вероятностных итеративных алгоритмов (алгоритмов адаптации) обратимся к условию оптимальности (7.4), которое с учетом (7.1) запишем в виде
∇J(c) = My{∇cF(y,c)} = 0, (7.8)
где 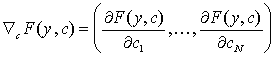 , представляет собой градиент F(y,c) по с.
, представляет собой градиент F(y,c) по с.
В (7.8) нам неизвестен градиент функционала, т.е. ∇J(c), а известны лишь реализации ∇cF(y,c) . В этом как раз и заключена центральная идея вероятностных итеративных алгоритмов. Следовательно, вероятностный итеративный алгоритм оптимизации (алгоритм адаптации) можно представить в рекуррентной форме
с[n] = с[n-1] - γ[n]∇cF(y[n], c[n-1]) , (7.9)
в разностной форме
∆c[n-1] = - γ[n]∇cF(y[n], c[n-1]) (7.10)
или как непрерывный алгоритм
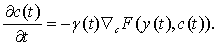 (7.11)
(7.11)
Легко видеть аналогию между регулярными итеративными алгоритмами (7.5) - (7.7) и вероятностными итеративными алгоритмами (7.9) - (7.11). Но в то же время они существенно отличаются друг от друга тем, что теперь
∇cF(y,c*) ≠ 0. (7.12)
Из-за этой особенности накладываются определенные условия на характер γ[n], чтобы обеспечить сходимость алгоритмов адаптации.
Оказалось, что этот подход позволяет решать самые разнообразные задачи:
- обучения опознаванию образов;
- определения характеристик динамических объектов (идентификация);
- обнаружения и выделения сигналов на фоне помех (фильтрация);
- в теории надежности;
- в исследовании операций;
- в теории игр;
- изучения поведения конечных автоматов.
Рассмотрим применение алгоритмических методов адаптации для управления динамическими объектами в условиях неопределенности.
| 7.2 Адаптивное управление |
Примем описание управляемого объекта в виде системы нелинейных разностных уравнений в векторной форме
y[n] = f(y[n-1], u[n-1]), (7.13)
где f(y,u )= (f1(y,u), ..., fl(y,u) - l-мерный вектор неизвестных функций;
y = (y1, …, yl) - вектор переменных состояния ОУ;
u = (u1, ..., um) - вектор управляющих воздействий.
УУ будем характеризовать законом управления
u[n] = φ(y[n]), (7.14)
где φ(y) = (φ1(y), ..., φm(y)) - m-мерный вектор неизвестных функций.
Переменные состояния и управляющего воздействия могут (или должны) подчиняться некоторым дополнительным ограничениям. Например,
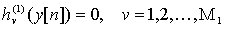 (7.15)
(7.15)
и 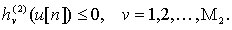 . (7.16)
. (7.16)
Пусть к системе приложено стационарное случайное задающее воздействие g[n]. Тогда критерием оптимальности может служить функционал
J1 = М{F1(g[n] - y[n])}, (7.17)
где F1(...) - некоторая выпуклая функция.
Задача состоит в определении такого закона управления (7.14), при котором переменные состояния и управляющие воздействия удовлетворяли бы ограничениям, а заданный критерий оптимальности (7.17) достигал минимума.
Особенность этой задачи, ее отличие от задач теории оптимального управления (как детерминированного, так и стохастического), состоит в том, что уравнения ОУ нам неизвестны и у нас нет достаточной априорной информации, на которую мы могли бы опереться, чтобы заранее рассчитать оптимальный закон управления.
| 7.2.1 Дуальное управление |
Недостаточность априорной информации приводит к необходимости совмещать изучение ОУ и управление им. Нельзя оптимально управлять объектом, не зная его характеристик, но можно изучать объект, управляя им, и тем самым иметь возможность улучшать управление, приближая его к оптимальному. В этой ситуации управляющие воздействия носят двойственный характер. Они служат как средством изучения, познавания объекта, так и средством направления его к желаемому (т.е. оптимальному), состоянию. Такое управление называют дуальным управлением. В системах дуального управления всегда существует противоречие между познавательной и направляющей сторонами управляющего воздействия. Очевидно, что двойственность знания и управления тесно связана с двойственностью прошлого и будущего. Можно обладать знанием о прошлом, но нельзя управлять им, и можно управлять будущим, не зная его.
Начнем с задачи изучения ОУ, т.е. задачи идентификации. Будем аппроксимировать каждую компоненту вектор-функции f(y,u) конечной суммой fi(у,u,с) = 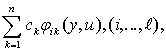 или в векторном виде f(у,u,с) = Ф(у,u)с, где Ф(у,u) = ||φik(y,u)|| (i=1, ..., l; k=1, ...1, N) - матрица линейно независимых функций φik(y,u) размера l x N .
или в векторном виде f(у,u,с) = Ф(у,u)с, где Ф(у,u) = ||φik(y,u)|| (i=1, ..., l; k=1, ...1, N) - матрица линейно независимых функций φik(y,u) размера l x N .
Задача идентификации объекта сводится к минимизации математического ожидания меры уклонения
J2(с)=М{F2[y[n] - Ф(y[n-1], u[n-1])c[n-1]]},
где F2(...) - строго выпуклая функция.
Минимизация J2(c) достигается с помощью следующего алгоритма:
c[n] = c[n-1] - γ2[n]∇cF2(y[n] - Ф(y[n-1], u[n-1])c[n-1]). (7.18)
Этот алгоритм можно назвать алгоритмом "изучения" и управляющее воздействие в нем не произвольно, а определяется законом управления, который принят в данный момент в системе. Примем закон управления в виде u[n] = ψ(y[n])b, где ψ=||ψvμ || (v=1, …, m; μ=1, …, M) - матрица размера m x M линейно-независимых функций, a b - вектор неизвестных коэффициентов управляющего устройства размерности М. Теперь критерий оптимальности (7.17) можно записать в виде
J1(b,c) = M{F1[g[n] - Ф(y[n-1], ψ(y[n-1])b)с]}
Оптимальный вектор b=b* соответствует минимуму J1(b,с). Естественно, b* существенно зависит от вектора с, определяющего характеристики управляемого объекта, и это подчеркнуто в обозначении аргументов формулы J1(b,c). Для нахождения оптимального вектора b* можно поступить так же, как и при определении оптимального вектора характеристик объекта с*, т.е.
b[n] = b[n-1] - γ1[n]∇bF1(g[n] - Ф(y[n-1], ψ(y[n-1])b[n-1])c[n-1]). (7.19)
Здесь значения с[n-1] определяются по алгоритму (7.18). Алгоритм (7.19) уместно назвать алгоритмом "управления".
Алгоритмы "изучения" и "управления" тесно связаны между собой. Это говорит о том, что процессы изучения и управления неразрывны, в чем и состоит суть дуального управления.
| 7.2.2 Поисковые адаптивные САУ |
Определим структурную схему адаптивной САУ с помощью поисковых алгоритмов дуального управления: алгоритма "изучения" (7.18) и алгоритма "управления" (7.19). Структурная схема рассматриваемой САУ (рис. 7.1) представляет собой объединение схем идентификации объекта и адаптивного фильтра, основанных на поисковых алгоритмах дуального управления. В адаптивной САУ каждое новое значение состояния ОУ у[n] вызывает изменение параметров с[n] и b[n].
Возможны и другие стратегии "изучения" и "управления".
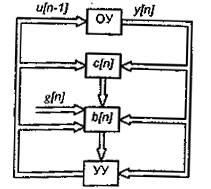
Рис. 7.1 - Адаптивная САУ
Например, изменение с[n] и b[n] можно производить после каждых l тактов, где l - предполагаемый порядок системы, т.е. число переменных состояния (фазовых координат) ОУ, либо по истечении такого числа тактов, когда можно с уверенностью считать, что при данных условиях определены действительно оптимальные значения векторов с* и b*
| 7.2.3 Беспоисковые адаптивные САУ |
Если невозможно или почему-либо нежелательно применять поиск, то можно осуществить синтез беспоисковой адаптивной системы управления на основе алгоритмов дуального управления (7.18) и (7.19).
Расшифровав в алгоритме управления (7.19) градиент реализации ∆bF1(...), можно заметить, что помимо известных функции 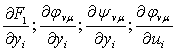 (так как функции F1(…), φvμ , ψvμ известны), в него войдут неизвестные функции
(так как функции F1(…), φvμ , ψvμ известны), в него войдут неизвестные функции 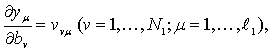 представляющие собой частные производные от выходной величины объекта по параметрам b. Эти функции называются функциями чувствительности. Они характеризуют влияние изменения параметров системы на процессы в ней и могут быть определены с помощью специальных моделей чувствительности.
представляющие собой частные производные от выходной величины объекта по параметрам b. Эти функции называются функциями чувствительности. Они характеризуют влияние изменения параметров системы на процессы в ней и могут быть определены с помощью специальных моделей чувствительности.
Для того чтобы не усложнять существа решаемой задачи деталями, ограничимся линейным ОУ, описываемым разностным уравнением вида
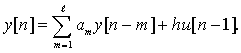 (7.20)
(7.20)
Вводя вектор коэффициентов
c = (a1, ..., al;h) (7.21)
и вектор ситуации
z[n] = (y[n-1], ..., y[n-l]; u[n-1]), (7.22)
запишем оценку у[п] в виде
y[n] = cTz[n]. (7.23)
Закон управления примем линейным:
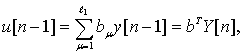 (7.24)
(7.24)
где b = (b1, ..., bl1) - вектор параметров УУ,
Y[n] = (y[n-1], ..., y[n-l1]) - вектор входных координат УУ.
Идентификация ОУ осуществляется с помощью алгоритма "изучения"
с[n] = с[n-1] + γ2[n]F2(x[n] - сT[n-1]z[n])z[n], (7.25)
который минимизирует функционал качества идентификации ОУ
J2(c) = M{F2(y[n] - cTz[n])}.
Если допустить, что dc[n]/db[n] ≈ 0, то алгоритм "управления" можно представить в следующем виде:
b[n] = b[n-1] + γ1[n]F1(g[n] - cT[n-1]z[n])Vb[n]c[n-1], (7.26)
где 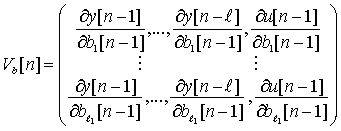 - матрица функций чувствительности размера l1х(l+1).
- матрица функций чувствительности размера l1х(l+1).
Если ввести матрицы
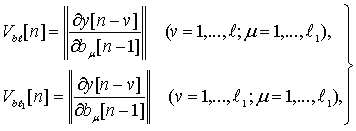
и вектор а=(a1,…,a?) - то алгоритм (7.26) можно записать в виде
b[n] = b[n-1] + γ1[n]F1(g[n] - сT[n-1]z[n])
(Vbl[n]а[n] + h[n]Vbl1[n]b[n-1] + h[n]Y[n]). (7.27)
Структурная схема адаптивной САУ, в основу которой положены алгоритмы (7.26) и (7.27), изображена на рис. 7.2 для случая, когда
l = l1 = 2.
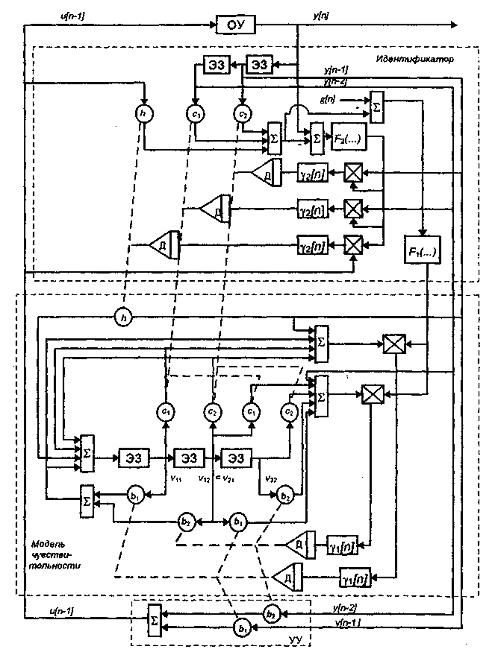
Рис. 7.2 - Беспоисковая адаптивная САУ
В эту схему входят Д-дигратор (дискретный интегратор, т.е. дискретный аналог интегратора) и модель чувствительности, которая заслуживает того, чтобы ее рассмотреть особо.
| 7.2.4 Модель чувствительности |
Модель чувствительности позволяет непосредственно определять функции чувствительности 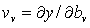 .Входом ее является выходная величина ОУ, а величины, снимаемые с определенных точек, равны искомым функциям чувствительности. Чтобы определить структуру модели чувствительности, продифференцируем обе части уравнения ОУ (7.20) по bv. Тогда, учитывая соотношение (7.24), получим следующее уравнение относительно функций чувствительности:
.Входом ее является выходная величина ОУ, а величины, снимаемые с определенных точек, равны искомым функциям чувствительности. Чтобы определить структуру модели чувствительности, продифференцируем обе части уравнения ОУ (7.20) по bv. Тогда, учитывая соотношение (7.24), получим следующее уравнение относительно функций чувствительности:
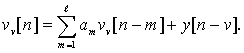 (7.28)
(7.28)
Оно внешне похоже на уравнение ОУ (7.20): выходной величине у[n] соответствует функция чувствительности, а управляющему воздействию hu[n-1] - выходная величина ОУ, запаздывающая на v тактов.
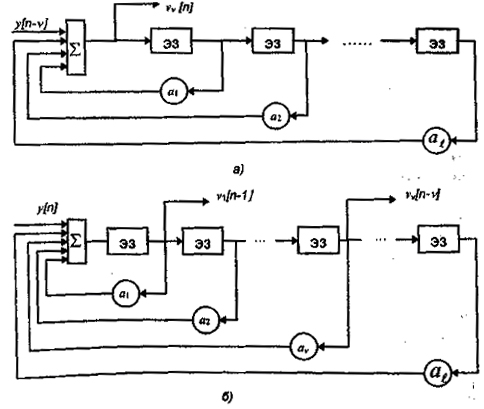
Рис. 7.3 - Модели чувствительности
Структурная схема модели чувствительности, описываемая уравнением (7.28) (рис. 7.3, а), представляет собой дискретный фильтр, на вход которого подается величина у[n-v], а ошибка представляет собой соответствующую функцию чувствительности. Структура модели чувствительности совпадает со структурой модели ОУ, описываемого линейным разностным уравнением. В общем случае для получения функции чувствительности vv[n] (v=1, ..., l) необходимо l моделей чувствительности. Но так как ОУ предполагается линейным с постоянными параметрами и, следовательно, уравнение чувствительности представляет собой уравнение с постоянными коэффициентами, то для получения всех функций чувствительности можно использовать лишь одну модель. Этот вывод следует из рис.7.3, б. На вход дискретного фильтра подается выходная величина объекта у[n], а с элементов запаздывания (ЭЗ) снимаются величины, соответствующие функциям чувствительности vv[n-m]. Аналогично можно составить модели чувствительности и для нелинейных ОУ. Но здесь уже нельзя обойтись одной моделью, как в случае линейного ОУ. Если бы удалось каким-то образом создать условия, при которых выходная и входная величины ОУ были бы независимы, то можно было бы использовать сам ОУ в качестве модели чувствительности.
Наиболее простым и известным типом адаптивной САУ является экстремальная система управления (ЭСУ) (см. рис. 1.12), а наиболее традиционный путь ее реализации представлен на рис. 5.17. Здесь УУ осуществляет поиск экстремума непосредственно на ОУ с помощью алгоритма (5.100). Задача адаптации возникает в связи с тем, что к ОУ (рис. 1.12) приложены воздействие g(t) и возмущение f(t), вызывающие "дрейф" экстремального значения зависимости (5.91). Дрейф экстремума может быть представлен "моделью блуждания" ЭСУ по графу состояний (см. рис. 5.18). Успешное решение задачи отслеживания дрейфующего экстремума функции (5.91) определяется правильным выбором величины ∆ в алгоритме (5.100). Применительно к схеме адаптивной САУ (см. рис. 7.1) дрейф экстремума задается функцией g[n], а величина ∆ является коэффициентом b[n]. Для настройки этой величины на оптимальное значение ∆*, которое в свою очередь зависит от скорости дрейфа экстремума, схему ЭСУ на рис. 5.17 следует дополнить вторым контуром управления. Таким образом, адаптивные САУ, кроме основного контура управления, содержат дополнительные контуры управления, которые осуществляют настройку структуры и параметров УУ. К настоящему времени наиболее совершенную форму имеет теория двухконтурного самоорганизующегося регулятора с экстраполяцией (СОРЭ), развитая А.А. Красовским Литературный комментарий поможет заинтересованному читателю более глубоко изучить данный тип адаптивной САУ.
| 7.3 Интеллектуальное управление |
Понятие "интеллектуальная система" возникло лет тридцать тому назад. Вначале под этим термином подразумевались системы, реализующие "антропоморфные функции". Данное определение оказалось неконструктивным, так как из него не следовали какие-нибудь предпосылки создания интеллектуальных управляющих систем. Но с течением времени развитие этого нового научного направления, получившего в дальнейшем название "искусственный интеллект", особенно таких его разделов, как инженерия знаний, компьютерные логика и лингвистика, когнитивная психология, методы поиска и принятия решений, модели обучения, подготовило теоретическую основу для создания программных систем по обработке и использованию знаний для успешного решения многих прикладных задач, включая создание систем, моделирующих творческие возможности человека. Такие системы стали называть "интеллектуальными", а применительно к области управления получил распространение термин "интеллектуальные системы управления". В структуре любой ИСУ содержатся следующие основные блоки: база знаний с развитыми механизмами вывода на знаниях, интеллектуальный решатель (формулирующий постановку и общий план решения задачи), интеллектуальный планировщик (формирующий конкретный план решения задачи), система объяснения и интерфейс с пользователем. ИСУ могут существенным образом различаться по структуре и выполняемым функциям, но в них в той или иной мере присутствуют перечисленные блоки. Иерархическая структура ИСУ соответствует базовому принципу, который считается в теории интеллектуальных систем фундаментальным. Принцип имеет аббревиатуру IPDI (Increasing Precision with Decreasing Itelligence) и сформулирован американским ученым Дж. Саридисом (учеником Я.З. Цыпкина) в 1989 г. и означает, что по мере продвижения к высшим уровням иерархической структуры ИСУ повышается интеллектуальность системы, но снижается ее точность, и наоборот. Иначе говоря: точность управления тем выше, чем меньше интеллектуальность уровня ИСУ, и наоборот, точность управления тем ниже, чем выше интеллектуальность данного уровня иерархии ИСУ. Для ИСУ справедливы следующие пять принципов:
- информационное взаимодействие ИСУ с реальным внешним миром с использованием специально организованных информационных каналов связи;
- принципиальная открытость системы для повышения интеллектуальности и совершенствования собственного поведения;
- наличие механизмов прогноза изменений внешнего мира и собственного поведения системы в динамически меняющемся внешнем мире;
- многоуровневая иерархическая структура, построенная в соответствии с правилом: повышение интеллектуальности и снижение требований к точности по мере повышения ранга иерархии в системе (и наоборот);
- сохраняемость функционирования (возможно с некоторой потерей качества или эффективности, т.е. с некоторой деградацией) при разрыве связей или потере управляющих воздействий от высших уровней иерархии.
Поясним кратко суть перечисленных принципов. Первый принцип подчеркивает непосредственную связь ИСУ с внешним миром. Находясь в непрерывном взаимодействии с внешним миром, ИСУ получает из него всю необходимую информацию для принятия решений и пополнения знаний. ИСУ, в свою очередь, может оказывать на внешний мир непосредственное активное воздействие в результате реализации собственного поведения. Модель знаний о внешнем мире ИСУ должна предполагать в этом смысле возможность изменений внешнего мира и знаний о нем в результате собственных на него воздействий. Принципиальная открытость систем в соответствии со вторым принципом обеспечивается наличием таких уровней высшего ранга в иерархической структуре ИСУ, как самонастройка, самоорганизация и самообучение. Система знаний ИСУ состоит из двух частей: постоянных (проверенных) знаний, которыми ИСУ обладает и постоянно пользуется, и временных (проверяемых) знаний, в которых система не уверена, с которыми она экспериментирует в процессе обучения. Знания второго типа либо отбрасываются ИСУ, либо переходят в знания первого типа в зависимости от результатов анализа своего поведения во внешнем мире. Выполнение второго принципа требует организации в ИСУ процесса приобретения и пополнения знаний. В соответствии с третьим принципом ИСУ нельзя считать в достаточной мере интеллектуальной, если она не обладает возможностью прогноза изменений самого внешнего мира и собственного в нем поведения (в динамически изменяющемся внешнем мире). Система без прогноза (функционирующая именно в динамически меняющемся внешнем мире) может попасть в критическую ситуацию, из которой не сможет найти выхода из-за временных ограничений на работу механизмов формирования управляющих воздействий, определяющих ее поведение, адекватное сложившейся ситуации. Примером могут служить автономно функционирующие интеллектуальные роботы в экстремальных ситуациях. Четвертый принцип позволяет наметить пути построения моделей ИСУ в тех случаях, когда неточность знаний о модели САУ или ее поведении можно скомпенсировать за счет увеличения числа уровней интеллектуальности, а также за счет использования совершенных механизмов принятия решений в условиях неопредленности в алгоритмах управления ИСУ. Пятый принцип устанавливает лишь частичную потерю интеллектуальности, но не прекращение функционирования при отказах в работе высших уровней иерархии ИСУ. Сохранение автономного функционирования в рамках более простого (автономного) поведения системы, характерного для нижних уровней структуры управления, также чрезвычайно важно для автономно функционирующих систем в реальном внешнем мире. Примером могут служить интеллектуальные роботы. Перечисленные пять принципов построения ИСУ позволяют ввести понятия "интеллектуальность в малом" и "интеллектуальность в большом".
Определение 7.1. ИСУ, организованные и функционирующие в соответствии с пятью принципами (в полном их объеме), называются ИСУ, обладающими свойством "интеллектуальности в большом".
Из определения 7.1 следует, что системы, обладающие свойством "интеллектуальности в большом", должны иметь многоуровневую иерархическую структуру со следующими уровнями (в порядке понижения ранга): самоорганизации (самоперестройки по результатам обучения); обучения; прогноза событий; адаптации; формирования решений; работы с базами событий и знаний; планирования операции по реализации сформированного решения; исполнительный. Каждый из перечисленных уровней имеет свою функциональную специфику и в реальной ИСУ может состоять из нескольких подуровней. При этом на самом нижнем исполнительном уровне обычно используются традиционные модели САУ. Все остальные уровни более высокого ранга можно рассматривать как надстройку над традиционными моделями. Минимальная надстройка может содержать всего лишь базу знаний, состоящую из нескольких продукционных правил. В этом простейшем случае могут отсутствовать уровни принятия решений и планирования.
Определение 7.2. ИСУ, структурно не организованные в соответствии с приведенными выше пятью принципами, но использующие при функционировании знания (например, в виде правил) как средство преодоления неопределенности входной информации, модели САУ или ее поведения, называются ИСУ, обладающими свойством "интеллектуальности в малом".
Определение 7.2 соответствует общепринятому определению интеллектуальной системы, ориентированной на обработку знаний с целью поиска решения задачи.
Определения 7.1 и 7.2 устанавливают границы уровней интеллектуальности ИСУ. Степень интеллектуальности ИСУ внутри этих границ можно определить по наличию или отсутствию тех или иных, введенных выше уровней. В ИСУ, интеллектуальных в большом, на верхних уровнях иерархической управляющей структуры используются, как правило, экспертные системы (рис.7.4). Структура ИСУ включает пять основных блоков.Блок "Интеллектуальный интерфейс" служит для связи с экспертом в области управления и используется в основном для обучения системы. Блок "Экспертная система" может быть представлен структурой, изображенной на рис. 7.5.
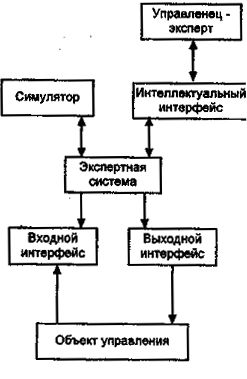
Рис. 7.4 - Структуры ИСУ, интеллектуальной в большом
Блок "Симулятор" осуществляет моделирование развития текущей ситуации (прогноз) и в некоторых случаях может выполнять функции анализа путей развития процессов, приведших к текущей ситуации (регноз).
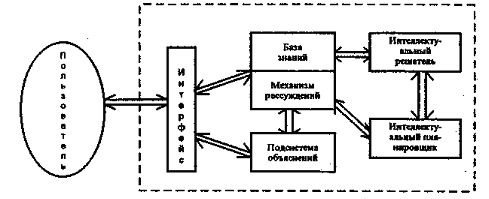
Рис. 7.5 - типовая структура экспертной системы
Структура ИСУ (рис. 7.4) может служить основой для построения многоуровневых структур логического управления. При этом функции исполнительного уровня будут реализованы в блоке "Выходной интерфейс". ИСУ на базе экспертной системы, снабженная механизмами обучения и прогноза развития текущих ситуаций, удовлетворяет пяти принципам построения ИСУ и, следовательно, относится к системам управления, обладающим свойством "интеллектуальности в большом". В настоящее время ведутся интенсивные исследования по созданию ИСУ на основе экспертных регуляторов, использующих технологию инженерии знаний и рассуждений на знаниях.
В структуре таких ИСУ (рис. 76), так же как и в структуре адаптивных САУ (см. рис. 7.1), кроме основного контура управления (УУ-ОУ) имеется так называемая интеллектуальная обратная связь с включенной в нее упрощенной экспертной системой.
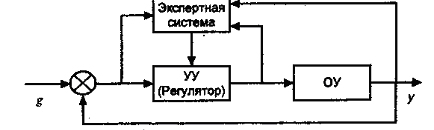
Рис. 7.6 - ИСУ с экспертным регулятором
Упрощение заключается в ориентации экспертной системы на решение управленческих задач, а также в отсутствии некоторых специфических блоков, присущих экспертным системам более широкого класса (например, подсистемам объяснения). С помощью экспертной системы осуществляется автоматическое управление коэффициентами УУ (регулятора) в зависимости от изменения характеристик внешней среды и ОУ. Основной проблемой при реализации экспертного регулятора является формирование базы знаний экспертной системы, получаемых в результате анализа динамических свойств системы в условиях изменения внешней среды и характеристик ОУ. Формирование базы знаний и организация эффективных механизмов вывода необходимы при разработке любой экспертной системы. Однако для экспертного регулятора проблема осложняется специфическими для САУ требованиями: высоким быстродействием и эффективностью поиска решений, удовлетворяющих целям управления; высокой надежностью (способностью обеспечивать эффективное функционирование системы управления в условиях неполностью определенной входной информации); гибкостью (способностью к подключению различных механизмов вывода на соответствующих фрагментах знаний) и компактностью (малыми массогабаритными характеристиками устройств, реализующих функции экспертной системы).
В заключение подчеркнем, что развитие технологии обработки информации оказывает существенное влияние на методы анализа и синтеза САУ. Особенно перспективно использование современной информационной технологии в ИСУ.
| Контрольные вопросы |
1. Суть понятий "детерминизм", "стохастичность", "адаптация", "интеллектуальность".
2. Критерий оптимальности и ограничения при неполной априорной информации.
3. Аналитические и алгоритмические методы решения задач теории управления.
4. Итеративные алгоритмы оптимизации.
5. Вероятностные итеративные алгоритмы адаптации.
6. Адаптивное управление (постановка задачи).
7. Дуальное управление. Алгоритмы дуального управления.
8. Структурная схема поисковой адаптивной САУ.
9. Беспоисковая адаптивная САУ.
10. Модели чувствительности.
11. Понятие об экстремальной системе управления.
12. Структура интеллектуальной системы.
13. Пять принципов построения ИСУ.
14. Интеллектуальность в "большом" и в "малом".
15. ИСУ с экспертной системой. Типовая структура экспертной системы. ИСУ с экспертным регулятором.
| Заключение |
Завершая изучение основ теории управления, попытаемся ответить на вопрос: достигнуты ли поставленные нами цели? В этой связи обратимся к Государственному образовательному стандарту высшего профессионального образования (ГОС ВПО), содержащему государственные требования к минимуму содержания и уровню подготовки выпускника по специальности "Программное обеспечение вычислительной техники и автоматизированных систем". Из ГОС ВПО следует, что изучив дисциплину "Основы теории управления" инженер должен:
- знать и уметь использовать основные положения теории управления, основные методы анализа и синтеза линейных непрерывных и дискретных систем управления;
- иметь представление об использовании основных положений теории управления в различных областях науки и техники.
Наше изложение основ теории управления не ограничивается описанием методов теории линейных систем управления. На практике разнообразные по своим свойствам системы в своем большинстве являются нелинейными, поэтому в настоящем учебном пособии изложены также элементы теории нелинейны<
Дата добавления: 2021-04-21; просмотров: 1083;











