Понятие о дискретном управлении

Задачи дискретного управления возникают в двух случаях: процесс управления по своей сути является дискретным; для управления непрерывным процессом используется дискретное управляющее устройство, в частности ЭВМ.
Дискретные регуляторы появились еще в прошлом столетии для регулирования паровых машин "на отсечку пара". Их исследование привело к рождению теории прерывистого регулирования на основе линейных разностных уравнений.
Позднее, в связи с появлением турбин и усовершенствованием паровых машин, регуляторы на отсечку потеряли свое значение, и интерес к теории дискретного управления на некоторое время ослаб.
В 20-е годы нашего столетия он возрождается в связи с созданием вибрационных и импульсных регуляторов электрических машин. Однако в определенных условиях работы динамические свойства импульсных и непрерывных линейных САУ достаточно хорошо совпадают, поэтому существенного развития теория дискретного управления в те годы не получила.
В 30-е годы интерес к дискретным системам усилился в связи с появлением регуляторов с падающей дужкой для медленных теплоэнергетических процессов. Действие этих регуляторов в какой-то степени аналогично действию человека, импульсами управляющего смесителем горячей и холодной воды при регулировании ее температуры: наблюдение за поведением системы во время паузы облегчает принятие решения о направлении и величине последующего импульса.
В регуляторах с падающей дужкой сравнительно просто и эффективно была решена проблема управления мощными сервомоторами от маломощных сигналов термопар.
Эти и аналогичные им устройства широко применяются для управления разнообразными объектами и в настоящее время.
В 40-е и 50-е годы в связи с развитием импульсной радиосвязи, радиолокации и вычислительной техники появляются дискретные САУ, использующие ЭВМ, и начинается новый этап развития теории дискретного управления.
Функциональная схема дискретной САУ не имеет принципиальных отличий от типовой схемы, представленной на рис. 1.7.
По сути, основное отличие дискретной САУ от непрерывной состоит в элементе ППЭ (см. рис. 1.7).
В дискретной САУ этот элемент является элементом дискретного действия, замыкающим и размыкающим контур управления. Далее данный элемент именуется ДЭ - дискретный элемент.
При комбинированном управлении возможно применение ДЭ и в качестве ПЭВ (см. рис. 1.7).
Во многих случаях схему дискретной САУ посредством переноса связей и воздействий, а также других преобразований удается привести к структурной схеме, представленной на рис. 5.1, где все элементы с непрерывными характеристиками и инерционными свойствами объединены в непрерывную часть (НЧ) системы, а безынерционный элемент дискретного действия представлен звеном ДЭ.

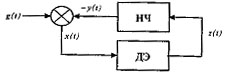
Рис. 5.1 - Дискретная САУ

Управляемая (регулируемая) величина y(t) на выходе НЧ, задающее воздействие g(t) и их разность - ошибка регулирования x(t) = g(t)-у(t) на входе ДЭ являются непрерывными функциями времени. ДЭ, часто называемый также импульсным элементом или аналого-цифровым преобразователем (АЦП), преобразует x(t) в последовательность импульсов z(t). Процесс преобразования непрерывной функции x(t) в дискретную z(t), осуществляемый ДЭ, называется квантованием. Различают три основных вида квантования: по времени, по уровню и комбинированное, сочетающее квантование по времени и по уровню. В соответствии с тремя способами квантования дискретные системы делят на три основных типа: импульсные, релейные и релейно-импульсные, или цифровые САУ. Отметим, что чаще всего под дискретными системами понимают только системы, в которых осуществляется квантование по времени, т.е. импульсные и цифровые, а релейные системы выделяют в особый тип САУ.
Рассмотрим способы квантования, наиболее распространенные в дискретных системах (рис. 5.2).

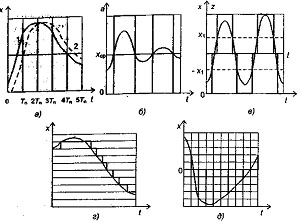
Рис. 5.2 - Квантование

На рис. 5.2, а квантование осуществляется по времени: значения непрерывной функции x(t) выделяются в дискретные моменты времени t_n(n = 0, ±1, ±2,...), называемые также моментами квантования. Квантование - это линейная операция. Моменты квантования часто отделены друг от друга равными промежутками времени, т.е. t_n = n•T , где T_n- период квантования (период чередования или повторения импульсов). Совокупность ординат х[n]=х(nT_n), n=0,1,2,..., называется решетчатой функцией, соответствующей непрерывной функции x(t). Решетчатая функция имеет дискретный аргумент, но ее ординаты могут принимать любые значения непрерывной функции. На рис. 5.2, б, в, г показано квантование функции по уровню. Выходная величина z(t) может принимать конечное множество значений, зависящих от достижения функцией x(t) некоторых пороговых значений. На рис.5.2,б пороговое значение только одно и равно величине срабатывания х_ср, поэтому при x(t) ≥ х_ср
z(t)= a = const; при x(t) < x_ср z(t) = 0.
Эта система относится к числу двухпозиционных релейных систем, реализующих принцип "включено - выключено". НА рис. 5.2, в представлена характеристика трехпозиционной релейной системы, имеющей два пороговых значения (+х₁, х₁) и зону нечувствительности между ними. На рис. 5.2, г показано квантование в многопозиционной релейной системе. Выходная величина ДЭ изменяется всякий раз, когда функция x(t) переходит через один из уровней квантования. На рис. 5.2, д показа но одновременное квантование по уровню и по времени. Значения функции фиксируются в равноотстоящие дискретные моменты времени пТп, при этом значения выходных величин округляются, например, до большего ближайшего уровня или до ближайшего меньшего уровня. Из трех основных типов дискретных САУ релейные системы являются существенно нелинейными, элементы теории которых были рассмотрены в разделе 4. В настоящем разделе изучим подробнее САУ, в которых осуществляется квантование по времени, т.е. импульсные и цифровые САУ. Для них главным в механизме квантования является квантование по времени. На рис. 5.2, а, д приведены примеры периодического квантования. Существуют и более сложные способы квантования. Например, в разных контурах управления могут использоваться разные периоды квантования. Такое квантование называется многочастотным и может рассматриваться как суперпозиция нескольких схем периодического квантования. Периодическое квантование изучено достаточно хорошо. В последние годы роль многочастотного квантования усиливается в связи с развитием многопроцессорных систем, а также в связи с техническими преимуществами использования разных частот квантования для различных переменных.
Рассмотрим особенности квантования в импульсных САУ. Прежде всего отметим, что для данного типа САУ ДЭ принято называть импульсным элементом (ИЭ). Квантование, осуществляемое ИЭ в виде преобразования непрерывного сигнала x(t) в последовательность импульсов z(t), называется импульсной модуляцией. Она заключается в изменении какого-либо параметра импульсов в зависимости от входного сигнала: амплитуды, длительности или момента начала действия импульса (обычно форма импульсов сохраняется при модуляции неизменной). В соответствии с этим различают три вида модуляции импульсов:

1) амплитудно-импульсную модуляцию (АИМ), при которой амплитуда импульсов а зависит от значения входного сигнала в момент начала действия импульса t_n (рис. 5.3), т.е. a(t_n) = k_ux(t_n)

Рис. 5.3 - Аплитудо-импульсная модуляция

2) широтно-импульсную модуляцию (ШИМ), при которой длительность импульса Т_u зависит от значения входного сигнала в момент начала действия импульса (рис. 5.4), т.е. T_u(t_n) = χx(t_n)

Рис. 5.4 - Широтно-импульсная модуляция

3) временную импульсную модуляцию (ВИМ), при которой временной сдвиг Т_с (запаздывание) импульса зависит от, значения входного сигнала в определенный момент времени (рис. 5.5), т.е. T_с(t_n) = χx(t_n).

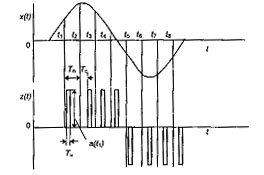
Рис. 5.5 - Временная импульсная модуляция

При АИМ и ШИМ модулирующий сигнал изменяет площадь (интенсивность) импульсов.
При ВИМ площадь импульса остается постоянной. Зависимость модулируемого параметра вырабатываемых импульсов от соответствующих дискретных значений входной переменной называется характеристикой ИЭ.
ИЭ с линейной характеристикой является линейным, а ИЭ с нелинейной характеристикой - нелинейным.
Обычно ИЭ работает периодически, вырабатывая по одному импульсу за каждый период.
Период следования импульсов T_n называется периодом повторения импульсов, или тактом дискретной системы. Величина ω = 2π/Т_п представляет собой частоту повторения импульсов.
Отношение длительности (средней в случае ШИМ) одного импульса к периоду повторения импульсов γ = Т_и/Т_п представляет собой относительную длительность импульсов. Величину 1 - γ принято называть скважностью ИЭ. Форма импульсов на выходе ИЭ может быть разной: прямоугольной, треугольной, совпадающей по форме с кривой x(t) во время импульсов и т.п. Для удобства исследования часто заменяют ИЭ, генерирующий импульсы сложной формы, последовательным соединением идеального ИЭ, генерирующего импульсы вида δ-функций, и формирователя, преобразующего δ-функцию в импульсы заданной формы.
Если на входе формирователя действует δ-функция k•δ(t),а z(t) - уравнение импульса на его выходе, то передается точная функция формирователя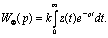
При линейной непрерывной части системы, имеющей передаточную функцию W_л(p), формирователь можно отнести к НЧ и считать, что НЧ имеет передаточную функцию
W_н(p) = W_ф(p)W_л(p).
Функциональная схема импульсной САУ по-прежнему будет иметь вид, представленный на рис. 5.1.
Перейдем к рассмотрению особенностей цифровых САУ.
При их реализации широко используются ЭВМ в роли управляющего устройства (рис. 5.6).

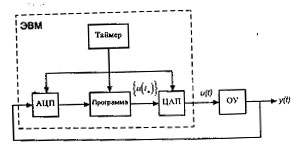
Рис. 5.6 - Цифровая САУ

Непрерывный выходной сигнал x(y) объекта управления преобразуется в цифровую форму АЦП. В зависимости от желания исследователя АЦП может рассматриваться как отдельное устройство или как составная часть ЭВМ.
Преобразование осуществляется в моменты квантования t_n и заключается в квантовании непрерывной величины по времени, по уровню и представлении полученных дискретных значений в виде чисел, т.е. в цифровом коде. В зависимости от принципа действия АЦП это преобразование может осуществляться либо путем последовательного выполнения перечисленных выше действий, либо сразу в виде одной операции. Описываемое преобразование называется кодоимпульсной модуляцией. Поэтому цифровые системы иногда именуют коде импульсными системами. Соответственно АЦ - преобразование называют кодированием, а обратное ЦА - преобразование - декодированием.
В отличие от импульсной модуляции, применяемой в импульсных САУ, в данном случае каждое значение преобразуемой входной величины представляется не одним импульсом модулируемый параметр которого (амплитуда - высота, длительность - ширина, момент начала действия импульса - фаза пропорционален входной величине, а серией импульсов. Каждое численное значение входной величины представляется определенной комбинацией этих импульсов, соответствующей дискретным значениям модулируемого параметра.
Существуют различные цифровые коды. Простейший из них - единичный код: каждое значение дискретной величины представляется числом импульсов, равным числовому значении величины. В случае десятичного кода дискретная величина выражается в виде десятичного числа и представляется серией импульсов, количество которых равно количеству разрядов этого числа. Каждый импульс несет информацию о цифре определенного разряда. Для этого модулируемый параметр импульса принимает одно из десяти дискретных значений.
Наибольшее распространение получил двоичный код: каждый разряд двоичного числа принимает одно из двух значение (0 или 1) и соответственно модулируемому параметру каждого импульса, представляющего значение одного из разрядов, тоже придается одно из двух крайних значений. Знак величины передается с помощью отдельного импульса с двумя возможными значениями модулируемого параметра.
В самом простом случае при учете только знака входной величины получается двухпозиционная релейная система с квантованием еще и по времени.
Преобразованный сигнал {y(t_n)} интерпретируется ЭВМ как последовательность чисел. ЭВМ обрабатывает эту последовательность по некоторому алгоритму и выдает новую последовательность чисел {y(t_n)} - которая преобразуется в непрерывный сигнал u(t) цифроаналоговым преобразователем (ЦАП). Заметим что САУ между ЦА- и АЦ- преобразователями разомкнута.
Таймер реального времени синхронизирует работу ЭВМ. Каждая операция в ЭВМ занимает определенное время, но на выходе ЦАП должен быть непрерывный по времени сигнал. ЦАП преобразует цифровые величины {u(t_n)} (см.рис.5.6) в ступенчатую функцию u(t)=u(nt_n), которая изменяется скачком в моменты t_n=nT_n, а в промежутке между этими моментами сохраняется неизменной или изменяется по определенному экстраполяционному закону (линейно, квадратично и т.д.).
Следовательно, управляющий сигнал u(nT_n) подобен квантованному по уровню сигналу с АИМ при γ = 1. Однако, если импульсные САУ могут быть как линейными, так и нелинейными, то наличие в цифровых САУ квантования по уровню делает их принципиально нелинейными, как и релейные САУ.
ЭВМ по-разному могут быть использованы для управления объектом или процессом, начиная от периодических вычислений вне контура управления и заканчивая работой в замкнутом контуре системы управления в реальном масштабе времени.
В настоящее время ЭВМ широко применяются для управления разнообразными объектами и процессами: технологическими процессами и производством, организационными и организационно-технологическими комплексами.
Условно можно выделить четыре этапа внедрения ЭВМ в системы управления: начальный этап; этап прямого цифрового управления; этап миникомпьютерной техники; этап микропроцессорной техники.
На 4-м этапе стоимость микрокомпьютеров резко снизилась и появилась возможность модульного наращивания их вычислительной мощности. Следовательно, становится реальным дискретное (цифровое) управление любым объектом независимо от его масштабов.
Развитие вычислительной техники стимулирует развитие теории управления и практическую реализацию все более сложных алгоритмов дискретного управления.