Автоматические системы с комбинированным управлением

4.9.1. Способы повышения точности автоматических систем. Одним из основных требований к автоматическим системам является точность. Чем выше точность, тем меньше ошибка воспроизведения задающего воздействия, меньше чувствительность системы к внешним возмущениям, лучше качество работы.

Повысить точность автоматических систем можно двумя способами:

1. Увеличением коэффициента усиления разомкнутой системы. При этом будут уменьшаться все коэффициенты ошибок, так как коэффициент усиления системы входит в знаменатель выражений всех коэффициентов ошибок. Однако, этот универсальный прием повышения точности приводит к снижению устойчивости и ухудшению качества работы в переходных режимах;

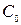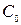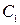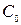
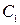
2. Повышением порядка астатизма. При этом становятся равными нулю младшие коэффициенты ошибок ( – в системах с астатизмом первого порядка; , – в системах с астатизмом второго порядка; 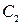– в системах с астатизмом третьего порядка и т.д.). Вследствие этого в этих системах не будет ошибки по положению, по положению и по скорости, по положению, скорости и ускорению и т.д.

Повышение порядка астатизма может быть достигнуто различными путями:

– Введением интеграторов в прямую цепь системы можно повысить порядок астатизма, как по входному сигналу, так и по возмущению. При этом интеграторы должны включаться до точки приложения возмущения, в часть системы с передаточной функцией 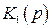(см. рис. 4.21).

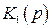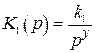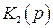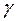Пусть содержит у интеграторов , а – интеграторов 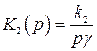. Передаточные функции по ошибке от входного сигнала и возмущения будут

,

.

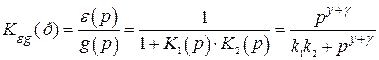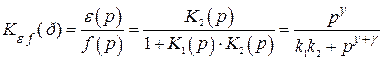Откуда видно, что порядок астатизма по задающему сигналу определяется общим числом интеграторов 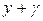, а по возмущению – числом интеграторов в 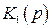до точки приложения возмущения. Следует отметить, что повышать порядок астатизма введением интеграторов возможно только в статических системах, так как каждый интегратор сдвигает фазовую характеристику на минус 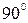и системы с двумя интеграторами становятся структурно неустойчивыми. При отсутствии в них форсировки фазовая характеристика, начинаясь с минус 180 градусов, заходит дальше при минимальной инерционности в прямой цепи, и система будет неустойчивой при любых величинах коэффициента усиления и постоянных времени.

– Введением изодромных устройств в прямую цепь системы (пропорционально–интегральных регуляторов). ПИ–регулятор представляет собой параллельное соединение интегратора с безинерционным звеном (см. рис. 4.22).

Передаточная функция такого регулятора

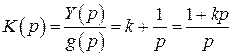(4.47)

можно трактовать как интегратор с форсирующим звеном. Постоянная времени форсировки определяется величиной коэффициента передачи безинерционного звена. Фазовая характеристика

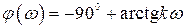. (4.48)

При соответствующем выборе 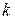фазовый сдвиг в области частоты среза системы можно сделать достаточно малым, и в этом случае ПИ–регулятор будет мало влиять на устойчивость системы.

– Комбинированным управлением, т.е. применением компенсирующих цепей для компенсации ошибок, обусловленных действием входного сигнала и возмущений.

4.9.2. Автоматические системы с комбинированным управлением. В системах с комбинированным управлением управление осуществляется как сигналом ошибки, так и компенсирующими сигналами, которые формируются из задающего воздействия и возмущений. Управление по ошибке происходит по замкнутому контуру, а управление по входному сигналу и возмущениям – по разомкнутому. Автоматические системы, в которых реализуется этот принцип управления по замкнутому и разомкнутому контурам, называются системами с комбинированным управлением. Структурные схемы систем с комбинированным управлением по входному сигналу и возмущению изображены на рис. 4.23 и 4.24 соответственно.

Рис. 4.23. Комбинированное управление по входному сигналу

Введение в систему компенсирующих цепей с передаточными функциями 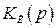теоретически позволяет получить абсолютную инвариантность системы, как по задающему воздействию, так и по возмущению, т.е. абсолютно точную систему, в которой ошибка равна нулю независимо от законов изменения сигналов.

В системах с комбинированным управлением по задающему сигналу (см. рис. 4.14) передаточная функция по ошибке

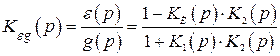, (4.49)

а передаточная функция замкнутой системы

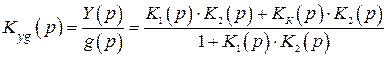. (4.50)

При выполнении условия

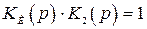(4.51)

передаточная функция по ошибке обращается в нуль, а передаточная функция замкнутой системы будет тождественно равна единице.

Условие (4.51) является условием абсолютной инвариантности по входному сигналу. При этом ошибка будет равна нулю при любом законе изменения сигнала.

В системах с комбинированным управлением по возмущению (см. рис. 4.15) передаточная функция по ошибке от возмущения

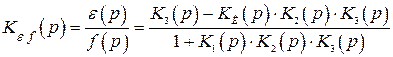. (4.52)

При выполнении условия

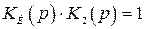(4.53)

она обращается в нуль. Это является условием абсолютной инвариантности систем по возмущению.

Условия абсолютной инвариантности легко объяснить из принципа работы по структурной схеме. Если в схеме на рис. 4.14 передаточная функция по цепи прохождения компенсирующего сигнала равна единице, т.е 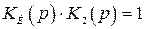, то выходной сигнал 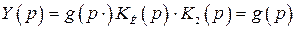будет полностью формироваться только по цепи компенсации ошибки. Сигнал же на входе 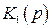, т.е. сигнал ошибки, при этом будет равен нулю.

В системах с комбинированным управлением по возмущению (см. рис. 4.15) при выполнении условия абсолютной инвариантности (4.53) сигналы на входе 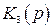, обусловленные действием возмущения 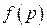, и 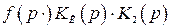будут равны и противоположны по знаку и компенсируют друг друга, т.е. действие возмущения будет скомпенсировано.

Замечательным свойством автоматических систем с комбинированным управлением является то, что компенсирующие цепи не изменяют характеристическое уравнение системы, а, следовательно, не влияют на устойчивость.

Следует отметить, что комбинированное управление позволяет уменьшить ошибку только по тому сигналу, по которому оно введено, т.е. комбинированное управление по входному сигналу позволяет уменьшить ошибку только от этого сигнала, и не влияет на ошибку от возмущения. Комбинированное управление по возмущению позволяет уменьшить ошибку только от этого возмущения, не влияя на ошибки от входного сигнала и других возмущений.

Условия абсолютной инвариантности (4.51) и (4.53) реализовать на практике не удается из-за физической нереализуемости требуемых передаточных функций, у которых порядок числителя должен быть выше порядка знаменателя. Приближенная реализация условий (4.51) и (4.53) позволяет получить частичную инвариантность (инвариантность до 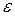). При этом повышается порядок астатизма системы, и она становится инвариантной к определенным видам воздействия (инвариантной к скорости изменения сигнала, инвариантной к ускорению и т.д.).

Рассмотрим возможность компенсации ошибки на примере системы с комбинированным управлением по входному сигналу (см. рис. 4.14). Часть системы с передаточной функцией 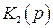является исполнительной, силовой частью системы. В нее входят исполнительный двигатель с редуктором, усилитель мощности, являющиеся наиболее инерционными силовыми элементами. Передаточная функция этой части обычно содержит интегратор и несколько инерционных звеньев:

,

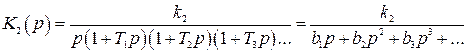где , , …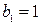

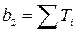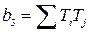Для выполнения условия инвариантности (4.51) передаточная функция компенсирующей цепи должна быть

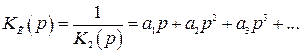, (4.54)

где , , …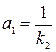

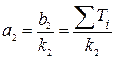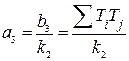На выходе 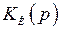должен формироваться сигнал, пропорциональный производным входного сигнала, причем число производных определяется порядком знаменателя .

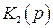Передаточная функция по ошибке

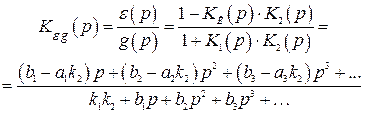(4.55)

Приравняв к нулю коэффициенты числителя, получим условия повышения порядка астатизма. Так, если в компенсирующей цепи реализовать только один дифференциатор с передаточной функцией

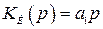, (4.56)

коэффициент передачи которого 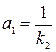, то порядок астатизма системы повысится на единицу и система станет с астатизмом второго порядка.

Если в компенсирующей цепи реализовать

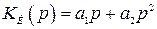, (4.57)

и установить коэффициенты передачи 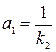, , 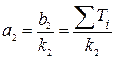то астатизм повысится на два порядка.

Астатизм системы повысится на три порядка при условии

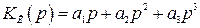, (4.58)

где , , .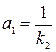

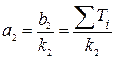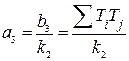Реализовать компенсирующую цепь с передаточной функцией 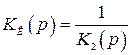практически не удается. Если первую производную входного сигнала (угла поворота командной оси) сравнительно легко получить с помощью тахогенератора, то вторую и высшие производные можно получить дифференцированием выходного сигнала тахогенератора, которое может быть выполнено лишь приближенно. Реальные дифференциаторы реализуют передаточную функцию вида

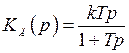, (4.59)

поэтому на каждую производную получается дополнительная паразитная инерционность. Реально реализуемая передаточная функция компенсирующей цепи получается в виде

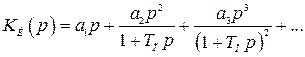. (4.60)

Наличие баластных постоянных времени в передаточной функции компенсирующей цепи влияет на условия компенсации ошибки и повышения порядка астатизма, а также на характеристическое уравнение замкнутой системы, повышая его порядок.

Отрицательной стороной комбинированного управления по задающему воздейсвию является существенное ухудшение качества переходных характеристик и некоторое увеличение их длительности. Увеличение порядка астатизма по управлению выше единицы не требуется для подавляющего числа приложений. В электроприводе с комбинированым управлением от использования ПИ-регулятора скорости всячески борются, устраняя его задатчиком интенсивности управляющего сигнала. Всегда комбинированое управление создает нули в передаточной фукнции замкнутой системы, и если они не сокращаются с полюсами, качество управления ухудшается. В хорошо спроектированной замкнутой системе нулей быть не должно.

4.9.3. Оценивание возмущений без установки дополнительных датчиков. Напротив, комбинирование управление по возмущению всегда имеет смысл. При этом вовсе не обязательно устанавливать датчики для каждого возмущения. Можно вообще возмущения не измерять непосредственно, а оценивать их интегральное воздействие с помощью наблюдателя, работающего от штатного датчика обратной связи. Для этого модель объекта в наблюдателе дополняем интегратором, воздействующим на вход модели. Порядок регулятора наблюдателя увеличится на единицу для подачи сигнала на вход интегратора. Регулятор наблюдателя L по рассогласованию выходов объекта и модели выделит на интеграторе оценку суммарного воздействия всех возмущений, приведенных к входу объекта. Схема модели объекта с регуляторами объекта K, наблюдателя L и оценивателем неизмеряемых возмущений приведена на рис. 4.25.

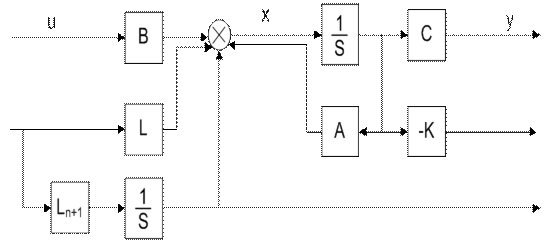
Рис. 4.25.

Остается сигнал с выхода интегратора подать со знаком минус на вход объекта, и те самым компенсировать все возможные возмущения без их непосредственного измерения. Таким путем обеспечивается астатизм по возмущению первого порядка для всех возможных возмущений, а не для одного конкретного. При этом не требуется устанавливать дополнительные измерители возмущений.

Для обеспечения астатизма второго порядка по возмущению, если уж таковой кому-то понадобится, модель в наблюдателе дополняется не одним, а двумя последовательно включенными интеграторами. Издержками будут более сложный регулятор наблюдателя и более медленный процесс оценивания.

4.9.4. Методы расчета систем с комбинированным управлением. При синтезе систем с комбинированным управлением решаются две задачи:

– Синтез параметров системы и необходимых корректирующих устройств для обеспечения требуемых устойчивости и качества регулирования в переходных процессах.

– Синтез структуры и параметров компенсирующей цепи, обеспечивающие требуемый порядок астатизма и точность.

Так как компенсирующая цепь влияет на точность и не оказывает существенного влияния на устойчивость, задача синтеза может быть решена по частям.

На первом этапе решается задача обеспечения устойчивости и качества замкнутого контура без предъявления требований к точности, а на втором этапе производится синтез компенсирующей цепи из условия обеспечения заданной точности. Задача синтеза может быть решена как аналитически (по частям), так и методом эквивалентных ЛАХ.

При аналитическом методе последовательность расчета может быть следующей:

1. По заданным требованиям к устойчивости и качеству работы в переходных режимах определяют параметры системы, обеспечивающие получение заданной устойчивости и качества, не обращая особого внимания на точность, что может быть обеспечено выбором соответствующего коэффициента усиления. Так в системе, не содержащей форсирующих звеньев, с передаточной функцией 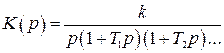для получения требуемого показателя колебательности М коэффициент усиления должен быть [6]

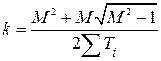. (4.61)

2. Определяют передаточную функцию по ошибке и коэффициенты ошибок в системе без комбинированного управления с рассчитанным коэффициентом усиления.

3. Рассчитывают величины ошибок по положению, скорости, ускорению и высшим производным.

4. Сравнивая рассчитанные ошибки с допустимой, определяют, какие из них должны быть компенсированы, т.е. определяют, сколько производных должно быть реализовано в компенсирующей цепи.

5. Определяют реально реализуемую передаточную функцию компенсирующей цепи.

6. Определяют передаточную функцию по ошибке в системе с комбинированным управлением и реально реализуемой передаточной функцией компенсирующей цепи.

7. Приравнивая к нулю коэффициенты числителя полученной передаточной функции, определяют условия компенсации ошибок, превышающих допустимую, т.е. определяют условия повышения порядка астатизма.

8. Выбирают схемную реализацию и рассчитывают параметры компенсирующей цепи.

При расчете систем с комбинированным управлением обычно используют ЛАХ несимметричного вида, у которых с повышением частоты наклоны возрастают (–1, –2, –3 и т.д.). Для таких ЛАХ проще получить большие значения добротностей по скорости, ускорению и высшим производным, что облегчает реализацию компенсирующих цепей.

Комбинированное управление в системе с регулятором в обратной связи. Регуляторы в обратной связи как модальный, так и линейно-квадратичный, если свести их к одному кубику (один вход, один выход), представляют собой сложные дифференцирующие модули с вычислением производных вплоть до (n – 1)-го порядка. Если стоит задача введения комбинированного управления по задающему воздействию, было бы непростительно не воспользоваться возможностями такого модуля. Вместо разработки и введения в систему управления специальных дифференцирующих блоков воспользуемся уже имеющимся в системе модулем гибкой обратной связи.

Для введения комбинированного управления переносим точку ввода задающего воздействия на вход модуля, что эквивалентно переносу регулятора из цепи обратной связи в прямую цепь. При этом приходится инвертировать задающее воздействие. Не вводя никаких новых элементов в систему, и не производя никаких расчетов, получаем очень мощное комбинированное управление, чаще всего чрезмерно мощное. Чрезмерность его проявляется в сильном возрастании перерегулирования и показателя M колебательности АЧХ.

Для уменьшения чрезмерного эффекта дозируем комбинированное управление коэффициентом ky < 1, подавая на вход дифференцирующего модуля лишь часть задающего воздействия. На прежний вход системы управления через коэффициент (1 – ky) подаем оставшуюся часть задающего воздействия. Таким способом по двухканальной схеме производим регулирование комбинированного управления изменением коэффициента ky. Схема с регулируемым комбинированным управлением изображена на рис. 4.26.

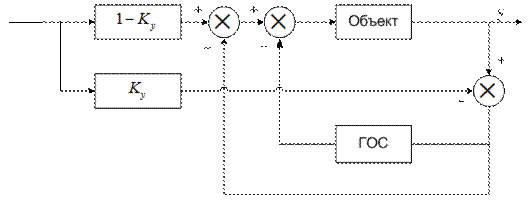
Рис. 4.26.

Критерием выбора коэффициента ky целесообразно выбрать показатель M колебательности АЧХ замкнутой системы, вычисляемый в Матлабе командой norm. Регуляторы в обратной связи обычно обеспечивают показатель колебательности M = 1. Последовательно увеличивая коэффициент ky, улавливаем начало превышения единицы показателем колебательности. Останавливаемся на границе или вблизи ее. Что обычно гарантирует небольшое перерегулирование (3 – 7) % переходной характеристики и улучшение интегральной квадратичной оценки в 2, 3 раза, интегральной модульной оценки в 1.5 раза.

На рис. 4.27. изображены переходные характеристики системы управления с регулятором в обратной связи (красная), с тем же регулятором в прямой цепи (голубая) и дозированным комбинированным управлением (зеленая).

Рис. 4.27.

Из графиков видно, что динамическая точностость систем с комбинированным управлением выше, интегральные оценки ошибок меньше.

На рис. 4.28. изображены ЛАХ вышеупомянутых замкнутых систем управления с той же маркировкой.

Рис. 4.28.

Из графиков видно, что полоса пропускания систем с комбинированным управлением значительно расширяется, в то же время как показатель колебательности удается сохранить вблизи единицы путем дозирования комбинированного управления.

Следует иметь в виду, что красивые переходные процессы систем с комбинированным управлением соответствуют процессам в малом. Физические ограничения на уровень сигнала управления объектом при комбинированном управлении срабатывают чаще и раньше из-за мощного дифференцирования.

4.9.6. Комбинированное управление в системе регулирования с наблюдателем.Регуляторы в обратной связи очень часто работают вместе с наблюдателем. Комбинированное управление по задающему воздействию, в таком случае, следует заводить на вход регулятора наблюдателя в инверсном виде, вместе с сигналом ошибки оценивания сигнала датчика. Схема изображена на рис. 4.29.

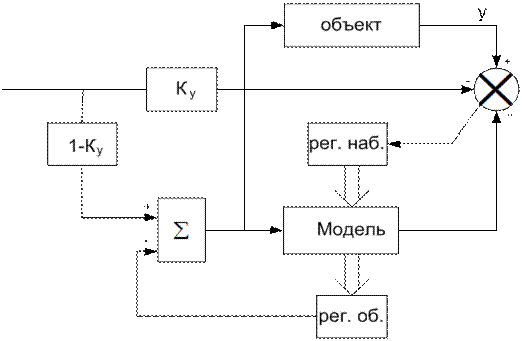
Рис. 4.29

Эффективность комбинированного управления через наблюдатель зависит от динамики наблюдателя относительно динамики управления объектом. При более быстром, чем замкнутый объект управления, наблюдателе эффект комбинированного управления значителен, при более медленном – эффекта может не быть вовсе. Дополнительная подстройка комбинированного управления коэффициентом ky позволяет устанавливать показатель колебательности M на желаемом уровне чуть больше единицы и получать в меру форсированную систему управления с малым перерегулированием переходной характеристики. Такая организация комбинированного управления по задающему воздействию не требует никаких дополнительных технических средств.