Описание дискретных систем в пространстве состояний
Проблему описания непрерывной системы, связанной с ЭВМ АЦ - и ЦА - преобразователями, рассмотрим на примере (рис. 5,10).
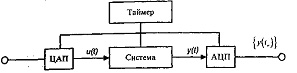
Рис. 5.10 - Непрерывная система соединенная с АЦ - и ЦА преобразователями
Определим зависимость между сигналами в ЭВМ, представляющими собой рассмотренные выше (рис.5.2, д; рис. 5.6) последовательности {u(tn)} и {y(tn)}. Пусть непрерывная система задана уравнениями состояния вида (2.42). Обычно при цифровом управлении АЦП сохраняет уровень аналогового сигнала постоянным до тех пор, пока не потребуется новое преобразование, поэтому моменты квантования tnможно определить как время, когда меняется управляющее воздействие. Следовательно, управляющий сигнал является дискретным процессом {u(tn): n=…-1,0,1,...}.
Определим связь между переменными системы в моменты квантования. Если состояние системы в момент квантования tn задано, то ее состояние в некоторый момент t можно получить, решив систему уравнений (2.42):
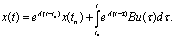 (5.51)
(5.51)
На основании (5.51) вектор состояния системы в момент квантования tn+1 определяется следующим образом
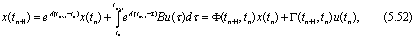
где 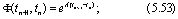
При определении второго слагаемого в (5.52) учтено, что u не изменяется в течение периода квантования. Из (5.52) следует, что вектор состояния в момент времени tn+1 есть линейная функция от x(tn) и u(tn). Если АЦП и ЦАП абсолютно синхронизированы и время преобразования незначительно, то можно считать, что переменные и и у квантуются в одни и те же моменты времени. Тогда уравнения, описывающие дискретную линейную систему в пространстве состояний, примут следующий вид:
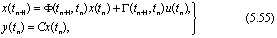
где Ф(tn+1, tn), Г(tn+1, tn) определены формулами (5.53) и (5.54).
Отметим, что уравнения (5.55) не приближенные, так как они дают точные значения переменных состояния и выходных переменных в моменты квантования, поскольку управляющие воздействие постоянно в период квантования. Поэтому уравнения (5.55) называют квантованием в приближении нулевого порядка системы уравнений (2.42). Систему (5.55) называют также эквивалентом системы (2.42) в приближении нулевого порядка.
Для квантования с периодом Т, tn = nTn, уравнения (5.55) описывают стационарную дискретную линейную систем поэтому
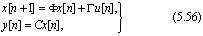
где 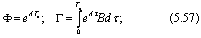
x[n] = x(nTn); y[n] = y(nTn); u[n] =u(nTn). (5.58)
Система уравнений (5.56) решается на основе следующих итераций:
x[n0+1] = Фx[n0] + Гu[n0],
x[n0+2] = Фx[n0+1] + Гu[n0+1] = Ф2x[n0] + ФГu[n0] + Гu[n0+1],
…
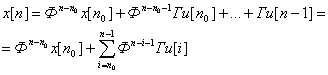 (5.59)
(5.59)
В полученном решении уравнения состояния две части: первая часть зависит от начальных условий, вторая является взвешенной суммой управляющих (входных) воздействий.
Инверсия квантования. Квантование определяет отображение непрерывных систем типа (2.42) в дискретные типа (5.56). Следующий простой пример показывает, что это отображение не всегда обратимо: не существует дифференциального уравнения первого порядка, которое после квантования приводило бы к разностному уравнению х[n+1] = -0,5x[n]+u[n], так как уравнение еa = -0,5 не имеет действительного решения, поскольку экспоненциальная функция всегда положительна.
Следовательно, модель (5.56) более общая, чем (2.42). Однако, если матрица Ф не имеет действительных отрицательных собственных значений, то существует соответствующая непрерывная система.
Поведение системы между моментами квантования. Дискретные модели (5.55) и (5.56) позволяют определить значения переменных состояния и выходных переменных в моменты квантования {tn}. Однако представляют интерес их значения между моментами квантования. Эти значения можно определить на основе выражения (5.51), которое можно переписать в виде
x(t) = Ф(t, tn)x(tn) + Г(t, tn)u(tn), (5.60)
где 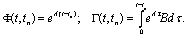
В пространстве состояний можно ввести новые координаты состояний и на этой основе осуществить преобразование моделей систем. Пусть S-невырожденная матрица и определят новый вектор состояния v[n] = Sx[n]. Тогда
v[n+1] = Sx[n+1] = SФх[п] + SГu[n ]=
= SФS-1v[n] + SГu[n] = 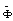 v[n] +
v[n] + 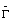 u[n]
u[n]
и y[n] =Сх[п] = CS-1v[n] = 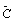 v[п].
v[п].
Следовательно, матрицы Ф, Г и С зависят от выбора координат для описания состояния системы. Интерес представляют инварианты, полученные после преобразования.
Теорема 5.1. Характеристическое уравнение D(λ) = |Ф - λE| = 0 является инвариантом, если новые состояния вводятся через невырожденную матрицу преобразования S.
Доказательство
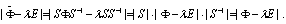
Новые координаты состояния системы вводятся для получения более простой формы уравнений, описывающих ее поведение.
Диагональная форма. Предположим, что матрица Ф имеет различные собственные значения. Тогда существует матрица S
такая, что 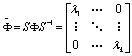 , где λ1 - собственные значения матрицы Ф. В результате преобразования получаете система разностных уравнений первого порядка:
, где λ1 - собственные значения матрицы Ф. В результате преобразования получаете система разностных уравнений первого порядка:
v1[n+l] = λ1v1[n] + β1u[n],
…
vk[n+1] = λ1v1[n] + β1u[n],
y[n] = γ1v1[n] + ... + γ1v1[n].
Решение этой системы уравнений имеет вид
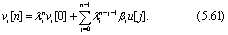
Если матрица Ф имеет кратные собственные значения то приводится к диагональной форме. В этом случае возможно приведение к жордановой форме. В жордановой форме преобразованная матрица 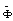 имеет собственные значения на главной диагонали и несколько единиц на наддиагонали.
имеет собственные значения на главной диагонали и несколько единиц на наддиагонали.
Наблюдаемая форма. Допустим, что характеристическое уравнения матрицы Ф имеет вид
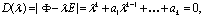 (5.62)
(5.62)
и что матрица
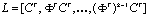 (5.63)
(5.63)
невырожденна. Тогда существует такая матрица преобразования S, что преобразованная система примет вид
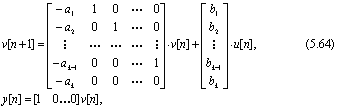
который называется наблюдаемой канонической формой. Примущества этой формы будут рассмотрены ниже.
Управляемая форма. Предположим, что характеристическое уравнение матрицы Ф определяется формулой (5.62), и что матрица
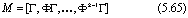
невырожденна. Тогда существует такое преобразование S, что преобразованная система примет вид:
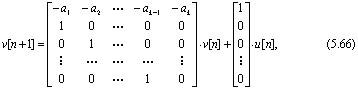
который называется управляемой канонической формой. Преимущество данной формы рассматриваются ниже.
Отметим, что наблюдаемую и управляемую формы также называют присоединенными (сопряженными).
Преобразование уравнений состояния в модели типа "вход - выход"
Весовую (импульсную переходную) функцию дискретной системы, описываемой моделью состояния (5.56), несложно определить из формулы (5.59):
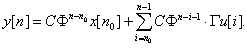
Из этого выражения следует, что импульсная переходная функция (в данном случае ее часто называют импульсной функцией) дискретной системы имеет вид
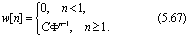
Теорема 5.2. Импульсная характеристика (5.67) инвариантна относительно линейного невырожденного преобразовав координат пространства состояний.
Доказательство.
Введем новые координаты v=Sx. Тогда импульсная характеристика преобразованной системы примет вид
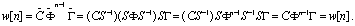
Определим передаточный оператор и передаточную функцию дискретной системы, описываемой моделью (5.56).
Для получения уравнения "вход-выход" исключим и (5.56) вектор состояния х[n+1] = qх[n] = Фх[n] + Ги[n], откуда (qE - Ф)х[n] = Гu[n]. В этих соотношениях q - оператор прямого сдвига. Тогда
y[n] = Cx[n] = C(qE - Ф)-1Гu[n]. (5.68)
Таким образом, передаточный оператор дискретной системы (5.56) имеет вид
W(q) = С(qЕ - Ф)-1Г. (5.69)
Этот оператор также можно выразить с помощью оператор обратного сдвига W*(q-1) = C(E - q-1Ф)q-1Г = W(q). Следовательно, передаточный оператор системы (5.56) является матрицей, элементы которой есть рациональные функции от q. Для одномерной системы получим
W(q) = C(qE - Ф)-1Г = P(q)/Q(q). (5.70)
Если размерность вектора состояния равна k, а многочлены Р(q) и Q(q) не имеют общих множителей, то степень многочлена Q равна k. Из (5.64) следует, что многочлен Q также является характеристическим многочленом матрицы Ф. Это означает, что модель "вход-выход" можно записать в виде уравнений (5.34), (5.35) и (5.41).
Теорема 5.3. Передаточный оператор W(q) для модели в пространство состояний не зависит от выбора координат пространства состояний.
Доказательство.
Пусть заданы передаточный оператор (5.69) и матрица преобразования S. В новых координатах
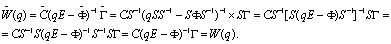
Упомянутое выше z-преобразование можно использовать для решения уравнений состояния (5.56). Применяя z-преобразование для обеих частей уравнения (5.56)
получим
z[X(z) - x(0)] = ФХ(г) + ГU(z),
X(z) = (zE - Ф)-1[zх(0) + ГU(z)],
Y(z) = C(zE - Ф)-1zx(0) + C(zE - Ф)-1ГU(z).
Следовательно, можно ввести передаточную функцию для системы (5.56) вида
W(z) = C(zE - Ф)-1Г. (5.71)
Это соотношение идентично (5.69) с заменой q на z. Осуществляя z-преобразование, получаем последовательность y[n]. Следовательно, справедлива следующая теорема.
Теорема 5.4. Импульсная характеристика (5.67) и импульсная передаточная функция связаны z-преобразованием.
| 5.3 Устойчивость дискретных систем |
Если выполнены условия известной теоремы Котельникова - Шеннона по неискаженной передаче непрерывного сигнала конечным числом его дискретных значений, то дискретная система сводится к непрерывной и, соответственно, ее устойчивость может исследоваться методами, изложенными в подразделах 3.2 и 4.3. Если эти условия не выполняются, то дискретная САУ должна исследоваться с учетом квантования по времени, т.е. на основе ее описания, изложенного в подразделе 5.2. При этом необходимо использовать или модели типа "вход-выход" (5.35), (5.41), (5.68) или модели пространства состояний (5.56).
| 5.3.1 Устойчивость дискретных линейных систем |
Используем общее необходимое и достаточное условие устойчивости линейных систем (3.38) и представление весовой функции дискретной линейной системы в форме (5.3). Подставляя (5.3) в (3.38), получим общее необходимое и достаточное условие устойчивости дискретной линейной системы
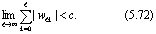
Для стационарной дискретной линейной системы wlk = wl-k, и заменой индекса суммирования на m = l-k условие (5.72) приводится к виду
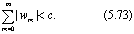
Следовательно, необходимым и достаточным условие устойчивости стационарной дискретной линейной системы является абсолютная сходимость ряда, членами которого являются ее весовые коэффициенты.
Импульсная передаточная функция стационарной дискретной линейной системы определяется формулой (5.20). Из сходимости ряда (5.73) следует, что ряд (5.20) сходится при z = 1. Но в таком случае он сходится при любом z-1, по модулю меньшем единицы, т.е. при |z|>1. Следовательно, импульсная передаточная функция устойчивой системы конечна всюду вне единичного круга плоскости комплексной переменной z с центром начале координат.
Таким образом, для устойчивости стационарной дискретной линейной системы необходимо и достаточно, чтобы все полюсы ее импульсной передаточной функции Ф(z) лежали внутри единичного круга с центром в начале координат.
В некоторых случаях импульсную передаточную функцию Ф(z) удобно рассматривать как функцию параметра 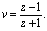 Данное соотношение называется преобразованием Мебиуса. Тогда
Данное соотношение называется преобразованием Мебиуса. Тогда

Обозначая импульсную передаточную функцию, рассматриваемую как функцию v, через Ω(v), получим
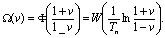
Преобразование Мебиуса отображает единичный круг на плоскости переменной z в левую полуплоскость переменной v. При этом окружность единичного радиуса плоскости z отображается в мнимую ось переменной v. Следовательно, для устойчивости стационарной дискретной линейной системы необходимо и достаточно, чтобы все полюсы ее передаточной функции Ω(v), рассматриваемой как функции комплексной переменной v, лежали в левой полуплоскости.
Отсюда следует, что к стационарным дискретным линейным системам применимы критерии устойчивости, рассмотренные в подразделе 3.2, но модифицированные с учетом особенностей описания дискретных систем.
Рассмотрим критерии устойчивости дискретных линейных систем с АИМ. Обозначим через 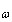 = ωТ - относительную частоту, через Ф(z)=Ф(
= ωТ - относительную частоту, через Ф(z)=Ф( 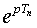 )=Ф(
)=Ф( 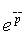 ) - импульсную передаточную функцию системы. Особенность дискретной передаточной функции Ф(
) - импульсную передаточную функцию системы. Особенность дискретной передаточной функции Ф( 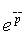 ) состоит в том, что она является периодической функцией мнимой части
) состоит в том, что она является периодической функцией мнимой части 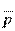 с периодом 2π, так как
с периодом 2π, так как 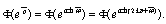
Физически периодичность частотной характеристики дискретной системы объясняется тем, что выходной сигнал ИЭ и, соответственно, воздействие на НЧ системы определяются значением входного сигнала только в дискретные моменты времени через промежуток времени Т.
Поэтому при гармоническом воздействии на ИЭ выходной сигнал системы не изменится при изменении частоты гармонического сигнала на любую величину, кратную  .
.
В результате при снятии частотной характеристики путем неограниченного увеличения частоты сигнала на выходе ИЭ должна получиться периодическая характеристика.
Передаточная функция Ф( 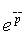 ) является периодически вдоль мнимой оси, поэтому при изучении ее полюсов на комплексной плоскости
) является периодически вдоль мнимой оси, поэтому при изучении ее полюсов на комплексной плоскости  достаточно рассмотреть их в полосе ±π вдоль действительной оси (рис. 5.11).
достаточно рассмотреть их в полосе ±π вдоль действительной оси (рис. 5.11).
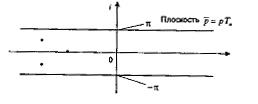
Рис. 5.11 - Расположение полюсов передаточной функции устойчивой дискретной системы
В изложенной трактовке условия устойчивости дискретных систем совпадают с условиями устойчивости непрерывных систем. Для применения критерия Рауса-Гурвица по-прежнему используется знаменатель Q(z) передаточной функции системы (5.48). Рассмотрим пример для системы первого порядка Q(z) = a0z + a1. Подставляя сюда (5.74), получим
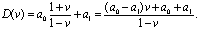
Соответствующее характеристическое уравнение имеет вид
(a0 - a1)γ + a0+a1=0,
и, следовательно, условия устойчивости Рауса-Гурвица, заключающиеся здесь в положительности коэффициентов характеристического уравнения, сведутся к неравенству а0 > а1.
Для системы второго порядка
Q(z) = a0z2+a1z+a2.
Соответственно.
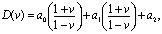
и характеристическое уравнение имеет вид
(a0 - a1 + a2)λ2+2(a0 - a2)λ+(a0 + a1 + a2)=0.
Из этого уравнения получаются следующие условия устойчивости: a0 - a1 + a2 > 0; a0 - a0 > 0; a0 + a1 + a2 > 0. Аналогично можно получить условия устойчивости для систем более высоких порядков, однако они оказываются сложнее, чем в случае непрерывных систем.
Критерий Найквиста для дискретных систем сохраняет прежнюю формулировку: условием устойчивости замкнутой системы, которая в разомкнутом состоянии устойчива, является неохват АФХ разомкнутой системы  точки (-1,i0) (рис.5.12).
точки (-1,i0) (рис.5.12).
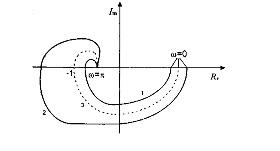
Рис 5.12 - Критерии устойчивости Найквиста для дискретной системы
На рисунке кривая 1 соответствует устойчивой системе, кривая 2- неустойчивой системе, а кривая 3-системе, находящейся на границе устойчивости. Разница по сравнению с непрерывным САУ заключается лишь в особенностях самих АФХ дискретных систем, которые строятся в диапазоне относительных частот 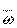 от 0 до π, поэтому данные характеристики не стягиваются в начало координат, а кончаются на действительной оси, как показано на рис. 5.12. Если разомкнутая система неустойчива, и функция W(
от 0 до π, поэтому данные характеристики не стягиваются в начало координат, а кончаются на действительной оси, как показано на рис. 5.12. Если разомкнутая система неустойчива, и функция W(  ) имеет k полюсов в правой полуполосе ±i?, то для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы конец вектора частотной характеристики W(i
) имеет k полюсов в правой полуполосе ±i?, то для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы конец вектора частотной характеристики W(i 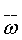 ) при возрастании
) при возрастании 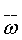 от 0 до π повернулся вокруг точки (-1, i0) вещественной оси в положительном населении k/2 раз. Критерий устойчивости Михайлова для дискретных систем требует, чтобы годограф
от 0 до π повернулся вокруг точки (-1, i0) вещественной оси в положительном населении k/2 раз. Критерий устойчивости Михайлова для дискретных систем требует, чтобы годограф 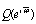 , представляющий собой знаменатель
, представляющий собой знаменатель  , начинаясь на положительной действительной полуоси комплексной плоскости
, начинаясь на положительной действительной полуоси комплексной плоскости  , охватывал начало координат, последовательно проходя 2n квадратов, где n - порядок системы (рис. 5.13).
, охватывал начало координат, последовательно проходя 2n квадратов, где n - порядок системы (рис. 5.13).
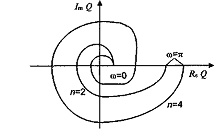
Рис. 5.13 - Критерий устойчивости Михайлова для дискретных систем
| 5.3.2 Устойчивость дискретных систем в пространстве состояний |
Рассмотрим дискретное уравнение движения в пространстве состояний
x[n+1] = F[x[n],n]. (5.75)
Уравнение (5.75) обобщает (5.56) на случай нестационарной и нелинейной дискретной системы.
Пусть х*[] и х[n] - решения (5.75) при начальных условиях х*[n0] и х[n0] соответственно.
Приведем следующие два определения устойчивости.
1. Решение х*[n] уравнения (5.75) устойчиво, если для заданного ε > 0 существует δ(ε, n0) такое, что для всех решений, удовлетворяющих условию
||x[n0] - x*[n0]|| < δ, ||x[n] - x*[n]|| < ε для всех n≥n0.
2. Решение х*[n] уравнения (5.75) асимптотически устойчиво, если оно устойчиво и если
||x[n] - x*[n]|| → 0 при n → ∞ , при условии, что
||x[n0] - x*[n0]||достаточно мало.
В этих определениях и далее ||•|| обозначает норму.
Из определений следует, что устойчивость, вообще говоря, определяется для конкретного решения (движения системы), а не для системы в целом.
Рассмотрим, в частности, устойчивость стационарной дискретной линейной системы, описываемой уравнением (5.56), свободное движение которой в пространстве состояний задано
уравнением
x*[n+1] = Фх*[n], х*[0]=a* . (5.76)
Для исследования устойчивости решения уравнения (5.76) изменим начальные условия.
Тогда получим
х[n+1] = Фх[n], х[0]=a .
Разность η = х - х* удовлетворяет уравнению
η[n+1] = Фη[n], η[0] = a - a*. (5.77)
Отсюда следует, что если решение х* устойчиво, то каждое другое решение также устойчиво, т.е. для стационарных дискретных линейных систем устойчивость - это свойство системы, а не конкретного движения системы.
Согласно (5.59) система (5.77) имеет решение
η[n] = Фnη[0]. (5.78)
Если матрицу Ф можно привести к диагональному виду, то решение является линейной комбинацией 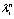 , где
, где 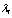 (i=1,... k) - собственные значения матрицы Ф (см. (5.61)). В общем случае, когда имеются кратные собственные значения матрицы Ф и ее диагонализация невозможна, решение (5.78) представляет собой линейную комбинацию рi[n]
(i=1,... k) - собственные значения матрицы Ф (см. (5.61)). В общем случае, когда имеются кратные собственные значения матрицы Ф и ее диагонализация невозможна, решение (5.78) представляет собой линейную комбинацию рi[n] 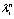 , где рi[п] - многочлен, порядок которого на единицу меньше кратности собственного значения
, где рi[п] - многочлен, порядок которого на единицу меньше кратности собственного значения 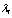 .
.
Для достижения асимптотической устойчивости все решения должны стремиться к нулю при n → ∞. Это возможно тогда и только тогда, когда | 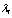 |<1, i=1,... n. Следовательно, справедлива следующая теорема.
|<1, i=1,... n. Следовательно, справедлива следующая теорема.
Теорема 5.5. Стационарная дискретная линейная система (5.76) асимптотически устойчива тогда и только тогда, когда все собственные значения матрицы Ф лежат строго внутри единичного круга.
Из приведенных рассуждений следует, что если дискретная линейная система асимптотически устойчива, то она устойчива и по условиям (3.38), (5.72), (5.73), т.е. ограниченный вход вызывает ограниченный выход при любых начальных условиях. Таким образом, асимптотическая устойчивость самое сильное условие, поэтому далее под устойчивостью понимается асимптотическая устойчивость.
Из теоремы 5.5 следует, что непосредственно проверку устойчивости исследуемой системы можно осуществить путем вычисления собственных значений матрицы Ф. Для этого созданы пакеты прикладных программ для ЭВМ. Однако этот метод нельзя применять, если матрица имеет параметры в своих элементах.
В ряде случаев проще исследовать характеристическое значение Q(z) = 0. Характеристический многочлен Q(z) является знаменателем импульсной передаточной функции (5.20), (5.48), (5.71). Проверка устойчивости осуществляется путем исследования условий, при которых корни многочлена попадают внутрь единичного круга. При этом используются как рассмотренные выше дискретные аналоги критериев Рауса-Гурвица, Найквиста, Михайлова, так и критерии Шура, Коха и Джури, эквивалентные критерию Рауса-Гурвица, а также хорошо известный метод корневого годографа.
| 5.3.3 Второй метод Ляпунова |
A.M. Ляпунов разработал свой метод для динамических систем, описываемых дифференциальными уравнениями (см. подраздел 4.3), но аналогичные теоремы и выводы, следующие из них, могут быть получены и для разностных уравнений.
Рассмотрим частный случай (5.69), когда движение системы в пространстве состояний описывается уравнением
x[n+1] = F[x[n]], F[0]=0. (5.79)
Функция V(x) является функцией Ляпунова для системы(5.79), если
V(x) непрерывна по x и V(0)=0 ;
V(x) положительно определена;
∆V(x) = V(F[0]) - V(x) отрицательно определена.
Теорема 5.6. Решение х[n] асимптотически устойчиво, если для системы (5.73) существует функция Ляпунова.
Кроме того, если 0 < φ(||х||) < V(x), где φ(||х||) → ∞ при ||x|| → ∞, то решение асимптотически устойчиво для любых начальных условий.
При использовании теоремы Ляпунова главная трудность состоит в построении подходящей функции Ляпунова. В общем случае это очень трудная задача, но для линейной системы (5.76) легко построить квадратичную функцию Ляпунова вида
V(x)xTAx. (5.80)
Проверим, является ли (5.80) функцией Ляпунова. Ее приращение равно
∆V(х) = V(Фх) - V(х)= хTФTАФх - хTАх = хT(ФTАФ -А)х = -хTВх.
Для того чтобы V(x) была функцией Ляпунова, необходимо и достаточно, чтобы существовала положительно определенная матрица А, удовлетворяющая уравнению
ФTАФ - А = -В, (5-81)
где В - положительно определена.
Уравнение (5.81) называется уравнением Ляпунова.
Доказано, что если линейная система устойчива, то уравнение (5.81) всегда имеет решение.
| 5.4 Устойчивость дискретных систем |
В подразделе 2.2 были сформулированы два фундаментальных свойства непрерывных динамических систем: управляемость и наблюдаемость. Первое свойство связано с возможностью перевода системы из заданного начального состояния в любое другое, а второе - с возможностью определения состояния динамической системы по наблюдаемым входам и выходам.
Рассмотрим эти свойства для дискретной системы, описываемой уравнением (5.56). Предположим, что задано ее начальное состояние х[0]. Тогда состояние системы в момент времени п (здесь п - порядок системы) определяется решением (5.59), которое в данном случае запишется в виде
x[n] = Фnx[0] + Фn-1Гu[0] + ... + Гu[n-1] = Фnx[0] + МU, (5.82)
где М = [ГФГ ... Фn-1Г]; U = [uT[n-l] ... ut[0]]T.
Если М имеет ранг n, то можно найти n уравнений, решение которых определит управляющий сигнал, переводящий системy из начального состояния х[0] в желаемое конечное состояние х[n]. Такое решение неединственно, если существует более одного входного сигнала.
Определение управляемости. Система (5.56) управляема, если существует управляющая последовательность, переводящая систему из любого начального состояния в начало координат за конечное время.
Матрицу М по аналогии с непрерывными системами называют матрицей управляемости.
С управляемостью тесно связано понятие достижимости.
Определение достижимости. Система достижима, если существует управляющая последовательность, переводящая систему из любого начального состояния в произвольное состояние за конечное время.
Управляемость не означает достижимость, что следует из уравнения (5.82). Если Фnx[0]=0, то нулевое состояние получается при нулевом входе, но система необязательно достижима. Однако эти понятия эквивалентны, если матрица Ф обратима.
Из определения достижимости следует, что система (5.56) достижима тогда и только тогда, когда матрица М имеет ранг n.
Нетрудно показать, что матрица управляемости не зависит от выбора системы координат в пространстве состояний. Допустим, что с помощью невырожденной матрицы преобразования S введены новые координаты. В этих координатах

Если М имеет ранг n, 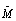 будет того же ранга. Следовательно, достижимость системы не зависит от выбора системы координат.
будет того же ранга. Следовательно, достижимость системы не зависит от выбора системы координат.
Из приведенных выше определений следует, что можно найти такую управляющую последовательность, что любое состояние достигается не более чем за n шагов (тактов дискретной системы). Означает ли при этом достижимость возможность отслеживания некоторой заданной траектории в пространстве состояний? Предположим, что из произвольного известного состояния x[k] систему надо перевести в состояние x[k+1]. Из (5.82) видно, что это выполнимо только в том случае, когда матрица Г имеет ранг n, т.е. необходимо, но не достаточно иметь п входных сигналов. В частном случае одномерной системы некоторое состояние можно получить только в каждой n-й точке квантования при условии, что оно известно за n шагов до него.
Задача отслеживания заданного выхода существенно проще. Предположим, что заданная траектория есть y0[k]. Тогда управляющее воздействие и должно удовлетворять условию
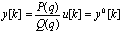 или
или 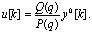 (5.83)
(5.83)
Предположим, что в системе существует временная задержка на d шагов. Тогда управление u[k] имеет причинный характер только тогда, когда требуемая траектория известна за d шагов. В этом случае управляющий сигнал вырабатывается в реальном времени. Таким образом, управляющее воздействие получают, подавая на вход обращенной системы Q(q)/P(q) требуемый выходной сигнал. Управление (5.83) имеет единственное решение, если сигнал y0[k] таков, что существует k0, при котором u[k]=0 для всех k<k0. Сигнал и ограничен, если сигнал у0 ограничен и обращенная система устойчива.
Для решения проблемы отыскания состояния системы по ее выходу вводится понятие ненаблюдаемых состояний: состояние х0 ≠ 0 ненаблюдаемо, если существует конечное k1 ≥ n-1, такое, что y[k]=0 для 0 ≤ k ≤ k1 при х[0] = х0 и u[k]=0 для 0 ≤ k ≤ k1.
Система (5.56) наблюдаема, если существует такое конечное k, что знания входов u[0],...,u[k -1] и выходов y[0],...,y[k-1] достаточно для определения ее начального состояния.
Рассмотрим систему (5.56). Действие известного входного сигнала всегда можно определить, и поэтому общность решения не пострадает, если предположить, что u[k]=0. Пусть даны y[0],y[1],...,y[k-1]Тогда можно записать следующую систему уравнений:
у[0] = Сх[0],
y[1] = Cx[1] = СФx[0],
…
y[n-1] = СФn-1x[0].
Векторная запись этой системы уравнений имеет вид
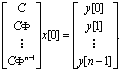 (5.84)
(5.84)
Состояние х[0] можно определить из (5.84) тогда и только тогда, когда матрица наблюдаемости
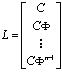 (5.85)
(5.85)
имеет ранг п. Состояние х[0] ненаблюдаемо, если принадлежит нуль-пространству L. Если два состояния ненаблюдаемы, то их линейная комбинация также ненаблюдаема. Следовательно, ненаблюдаемые состояния образуют линейное подпространство. Справедливо следующее утверждение: система (5.56) наблюдаема тогда и только тогда, когда L имеет ранг n. Аналогично (см. подраздел 2.2) определялась наблюдаемость для непрерывных систем. Легко показать, что матрица наблюдаемости, так же как и матрица управляемости, не зависит от выбора системы координат. Рассмотрим четыре примера на введенные понятия.
Пример 5.3. Система
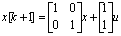
недостижима, так как
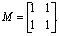
Если было бы два входа с невырожденной матрицей Г, то система достигала бы любого состояния за конечное время.
Пример 5.4. Пусть дана система
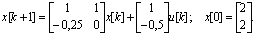
Можно ли найти такую управляющую последовательность, что хT[2] = [-0,5 1] ? Из уравнения (5.82) следует, что х[2]=Ф2х[0]+ФГu[0]+Гu[1], или
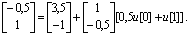
Отсюда получаем, что 0,5u[0] + и[1] = -4 .
Следовательно, одна допустимая управляющая последовательность существует: u[0] = -2 и и[1] = -3 . Предположим теперь, что хT[2] = [0,5 1]. Соответствующая система уравнений 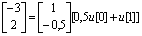 не имеет решения, так как система недостижима. Матрица управляемости имеет следующий вид:
не имеет решения, так как система недостижима. Матрица управляемости имеет следующий вид: 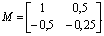
Из начала координат можно достичь только тех точек в пространстве состояний, которые принадлежат подпространству, "натянутому" на вектор [1 -0,5]T. Этот вывод следует из теоремы Гамильтона-Кэли, доказанной в теории матриц. Теорема утверждает, что если D(λ) (см. (2.43)) есть характеристическое уравнение матрицы А, тогда А удовлетворяет уравнению D(A) = 0, т.е. матрица А удовлетворяет собственному характеристическому уравнению. В силу теоремы Гамильтона-Кэли из (5.82) следует, что все состояния, достигаемые из начала координат, "натянуты" на столбец матрицы управляемости М. Это означает, что достижимые состояния принадлежат линейному подпространству, порождаемому столбцами матрицы М. В примере 5.4 достижимы и другие точки из-за влияния начального значения.
Пример 5.5. Рассмотрим систему третьего порядка (п=3)
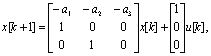
которая записана в управляемой форме. Матрица управляемости М и обратная матрица М-1 имеют вид:
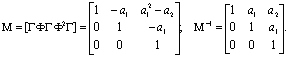
Пример 5.5 можно обобщить до порядка п, где
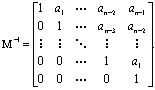
Пример 5.6. Рассмотрим систему
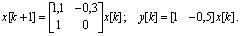
Представим графики выходной переменной для четырех различных начальных условий (рис. 5.14).
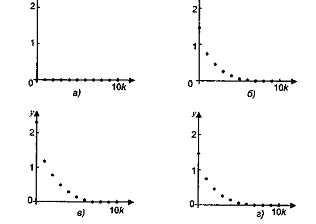
Рис. 5.14 - Выход системы, описанной в примере 5.6:
а - [0,5 1]; б - [1,5 0,5]; в - [2,5 0]; г - [1 -0,5]
Матрица наблюдаемости имеет вид 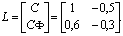 Ранг матрицы L равен 1 и наблюдаемые состояния принадлежат нуль-пространству L, т.е. [0,5 1] (рис. 5.14, а). Из рис. 5.14, б, в, г следует, что различные начальные состояния дают одинаковый выход, если они лежат на линии, параллельной линии, проходящей через состояние [0,5 1] и начало координат [0 0] (см. рис. 5.14, б, г).
Ранг матрицы L равен 1 и наблюдаемые состояния принадлежат нуль-пространству L, т.е. [0,5 1] (рис. 5.14, а). Из рис. 5.14, б, в, г следует, что различные начальные состояния дают одинаковый выход, если они лежат на линии, параллельной линии, проходящей через состояние [0,5 1] и начало координат [0 0] (см. рис. 5.14, б, г).
| 5.4.1 Декомпозиция Калмана |
Достижимая и ненаблюдаемая части дискретной системы - это два линейных подпространства в пространстве состояний. Они не зависят от выбора системы координат в пространстве состояний. Американский ученый Р. Калман показал, что существует такая система координат, в которой поведение дискретной системы описывается следующей блочной формой:
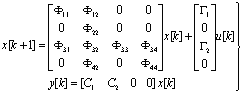 (5.86)
(5.86)
где Фij, Гi, Ci - матрицы соответствующего ранга.
Система уравнений (5.86) разлагается на четыре часта, каждая из которых соответствует достижимому и наблюдаемому, недости-жимому, но наблюдаемому, достижимому, но ненаблюдаемому, недостижимому и ненаблюдаемому состояниям. Р.Калман доказал следующую теорему.
Теорема 5.7. Линейная система может быть разложена на четыре подсистемы со следующими свойствами:
S1 - наблюдаемая и достижимая подсистема;
S2 - наблюдаемая, но недостижимая подсистема;
S3 - ненаблюдаемая, но достижимая подсистема;
S4 - ненаблюдаемая и недостижимая подсистема.
На основании этой теоремы дискретную систему представим схемой (рис. 5.15).
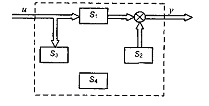
Рис. 5.15 - Декомпазиция Калмана
В результате несложных алгебраических преобразований импульсная передаточная функция системы может быть записана в виде 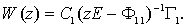 Таким образом, импульсная передаточная функция системы однозначно определяется наблюдаемой и достижимой частью системы (подсистемой S1,).
Таким образом, импульсная передаточная функция системы однозначно определяется наблюдаемой и достижимой частью системы (подсистемой S1,).
| 5.4.2 Потеря достижимости и наблюдаемости при квантовании |
Квантование непрерывной линейной системы дает дискретную систему с матрицами, ранг которых зависит от периода квантования. Проанализируем, как влияет период квантования на достижимость и наблюдаемость дискретной системы. Для получения достижимой дискретной системы необходимо, чтобы исходная непрерывная система также была достижима, так как допустимые управляющие сигналы дискретной системы (кусочно-постоянные сигналы) есть подмножество допустимых управляющих сигналов непрерывной системы. Однако для некоторых значений периода квантования достижимость теряется.
Условия ненаблюдаемости для непрерывной системы более строгие, так как выход должен быть равен нулю на некотором интервале времени, тогда как для дискретной системы выход должен быть равен нулю только в моменты квантования. Это значит, что непрерывный выход может колебаться между моментами квантования и быть равным нулю в эти моменты. Данное явление иногда называют скрытым колебанием. Таким образом, дискретная система может быть ненаблюдаема, даже если соответствующая непрерывная - наблюдаема.
Пример 5.7. Для иллюстрации изложенного рассмотрим модель гармонического осциллятора - математический маятник (рис. 5.16). Ускорение точки подвеса является входом, а угол отклонения нити - выходом.
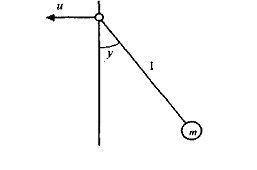
Рис. 5.16 - Маятник
Такая система описывается следующими нормализованными нелинейными уравнениями: 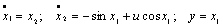 где x1 - угол отклонения; x2 - угловая скорость. Линеаризация уравнений в окрестности точки u = х1 = 0 дает
где x1 - угол отклонения; x2 - угловая скорость. Линеаризация уравнений в окрестности точки u = х1 = 0 дает
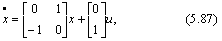
у = [1 0]х.
Передаточная функция для (5.87) имеет вид
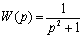
и в более общем виде -
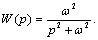
Для этой передаточной функции уравнения (5.87) перепишутся в следующем виде:
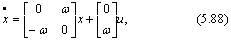
y=[1 0]х.
Система уравнений (5.88) может быть использована также для описания в первом приближении динамики подъемного крана.
Квантование (5.88) с фиксатором нулевого порядка приводит к следующей дискретной модели гармонического осциллятора:
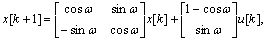 (5.89)
(5.89)
y[k] = [1 0]x[k].
Определители матриц управляемости и наблюдаемости системы (5.89) имеют вид:
detM = -sinω(l - cosω),
detL = sinω.
Достижимость и наблюдаемость дискретной системы (5.89) теряется при ω = nπ, тогда как соответствующая ей непрерывная система (5.88) управляема и наблюдаема.
| 5.5 Графовые модели дискретной нелинейной динамической системы |
Достоинства графического представления поведения систем управления в двухмерном пространстве состояний очевидны. Особенно очевидны эти преимущества при существующем уровне развития вычислительной техники и соответствующих возможностях графического представления разнообразной информации на мониторе (дисплее) ЭВМ. Однако реальные дискретные динамические системы имеют размерность пространства состояний существенно больше двухмерной. Наличие в их структуре нелинейностей создает дополнительные значительные трудности исследования таких систем. В этой связи преобразование пространства состояний дискретной нелинейной динамической системы любой конечной размерности к двухмерному, предложенное Г.А. Медведевым, представляет не только теоретический, но и практический интерес. Изложим его суть на примере дискретной нелинейной САУ (рис. 5.17).
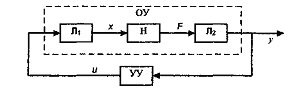
Рис. 5.17 - Дискретная нелинейная САУ
Реальный инерционный объект управления характеризуется тем,
Дата добавления: 2021-04-21; просмотров: 887;











