Описание дискретных систем разностными уравнениями

Рассматривая входную и выходную переменные дискретной системы только в определенные моменты времени t_n=nT_n (n=0,±1,±2,...), мы не имеем возможности давать времени бесконечно близкие значения и совершать предельные переходы, неограниченно сближая эти значения. Поэтому становится неудобным характеризовать скорость изменения функции ее производной. В этой связи, рассматривая поведение дискретных систем лишь в определенные равноотстоящие моменты времени, вместо производных используют конечные разности функций, а вместо дифференциальных уравнений - разностные уравнения.
Выражение
∆y[n] = ∆y(nT_n) =y((n+1)T_n) - y(nT_n) = y[n+1] - y[n] (5.28)
называется первой конечной разностью или конечной разностью первого порядка функции y(t)=(nТ_n) в точке t = nТ.
Аналогично определяются разности высших порядков. Так, ∆²у[n] = ∆(∆y[n]). Дважды применяя формулу (5.28), получим
∆²y[n] = {y[n+2] - y[n+1]} - {y[n+1] - y[n]} = y[n+2] - 2y[n+1] + y[n]. (5.29)
Заметим, что в (5.29) и далее используются введенные в (5.28) обозначения
y[n] = y(nT_n) (n=0,±1,±2,...), (5.30)
∆у[n]=у((n+1)Т_n)-y(nТ_n) (n=0,±1,±2,...). (5.31)
Если определена конечная разность (k - 1)-го порядка ∆^k-1y[n], то конечная разность k-го порядка есть ∆(∆^k-1y[n]). Методом полной математической индукции можно доказать формулу
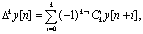(5.32)
где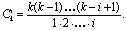

Формула (5.32) выражает конечную разность k-го порядка через значения функции y(t) = у(nТ_n) = у[п] в точках nТ_n, (n+1)T_n, …, (n+k)T. Можно получить также формулу, в которой y[n+k] = y((n+k)T_n) выражается через конечные разности этой функции в точке nТ_n. Для этого положим по определению ∆⁰y[n] = y[n]. Тогда y[n+1] = y[n] + ∆y[n] = ∆⁰y[n] + ∆⁰y[n]. Методом полной математической индукции легко доказывается формула

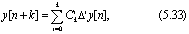
где 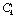- определенные выше биномиальные коэффициенты.
Соотношение, связывающее значения неизвестной функции у[n] и разностей различных порядков ∆y[n], ∆²y[n], ..., называется уравнением в конечных разностях или разностным уравнением. Если это соотношение линейно, то оно представляет собой линейное разностное уравнение.
Разностное уравнение может содержать или значения неизвестной функции и ее разностей различных порядков при одном и том же значении аргумента t=пТ, или значения неизвестной функции при различных равноотстоящих значениях аргумента. При помощи формул (5.32) и (5.33) можно преобразовать разностное уравнение из одной формы в другую. Разностное уравнение, содержащее разности неизвестной функции до k-го порядка или значения неизвестной функции от у[n] до y[n+k], называется разностным уравнением k- го порядка.
На основании вышеизложенного стационарная дискретная линейная система описывается линейным разностным уравнением вида
c₀∆^ky[n] + с₁∆^k-1y[n] + ... + с_k∆⁰y[n] =
=d₀∆^mx[n]+ d₁∆^m-1x[n] + ... + d_m∆⁰x[n] (5.34)
или вида
a₀y[n+k] + a₁y[n + (k-1)] + … + a_ky[n] =
= b₀x[n+m] + b₁x[n+(m-1)] + ... + b_mx[n] (5.35)
Для стационарной системы коэффициенты а_i и c_i (i=0,1,...k), b_j и d_j (j=0,1,…m), m<k, являются постоянными величинами, а для нестационарной - функциями времени, правая часть уравнении (5.34) и (5.35) - заданная функция.
Итак, получено описание дискретной системы разностными
уравнениями, использующими прямые (упреждающие) разности (5.28).
Аналогично выводятся разностные уравнения на основе обратных (отстающих) разностей
∇y[n] = y(nT_n) - y((n-1)T_n = y[n]-y[n-1]. (5.36)
В этом случае уравнения дискретной САУ имеют вид:
c₀∇^k[n] + c₁∇^k-1y[n] + ... + c_k∇⁰y[n]=
= d₀∇^mx[n]+ d₁∇^m-1x[n] + ... + d_m∇⁰x[n], (5.37)
a₀y[n] + a₁y[n-1] + … + a_ky[n-k] =
= b₀x[n] + b₁x[n-1] + ... + b_mx[n-m]. (5.38)
При исследовании непрерывных линейных систем, описываемых линейными дифференциальными уравнениями, удобно использовать оператор дифференцирования р = d/dt. Для систем, описываемых линейными разностными уравнениями, можно построить аналогичное операционное исчисление. Для задания оператора определяется класс входных сигналов и его действие на них. В операционном исчислении принято, что все сигналы - неограниченные справа и слева последовательности {у[n]: n=...-1,0,1,…}. Оператор прямого сдвига, обозначаемый через q, обладает следующим свойством:
qy[n] = y[n+1]. (5.39)
Инверсия оператора прямого сдвига называется опера тором обратного сдвига q^-1, который обладает следующим свойством: q^-1y[n] = y[n-1]. (5.40)
На основании формулы (5.39) уравнение (5.35) можно переписать в комплексной форме
Q(q)y[n] = P(q)x[n], (5.41)
где Q(q) и P(g) - полиномы относительно оператора сдвига:

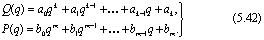
Определим передаточную функцию стационарной дискретной линейной системы, описываемой разностным уравнением (5.41). По определению передаточной функции, изложенному в подразделе 2.1, реакция такой системы на показательное возмущение
x(t) = e^pt, x[n] = 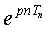(5.43)
определяется формулой
y[n] = Ф(z) 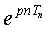. (5.44)
Подставляя (5.44) и (5.43) в (5.41), получим
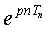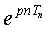Ф(z)Q(q) =P(q) . (5.45)
Согласно (5.39) имеем 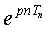q = q = = .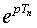
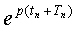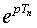
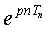Используя обозначение z = 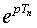перепишем это выражение в виде
q 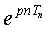= z 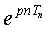, (5.46)
т.е. применение операции сдвига к показательной функции сводится к ее умножению на величину z. Следовательно,
q^lepnTn=z^lepnTn, (l=1,2,…). (5.47)
На основании формулы (5.47) мы можем заменить в уравнении (5.45) оператор q величиной z и получим алгебраическое уравнение для Ф(z). Сокращая это уравнение на 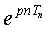и решая его, получим следующую формулу для передаточной функции системы, описываемой разностным уравнением (5.41):
Ф(z) = Р(z)/Q(z), (5.48)
Следовательно, передаточная функция стационарной дискретной линейной системы, поведение которой описывается разностными уравнениями, всегда является дробнорациональной функцией переменной z = .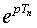
Таким образом, передаточные функции стационарных дискретных линейных систем, описываемых разностными уравнениями, определяются так же, как и передаточные функции непрерывных стационарных линейных систем, описываемых дифференциальными уравнениями. В непрерывной системе оператор дифференцирования в дифференциальном уравнении заменяется параметром показательной функции р, а в дискретной системе оператор сдвига в разностном уравнении заменяется величиной 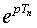. В обоих случаях в итоге получается алгебраическое уравнение для передаточной функции системы.
Отметим, что операторы дифференцирования и сдвига связаны тем же самым соотношением, что и величины р и z , т.е.
q = 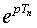. (5.49)
В (5.49) в показателе экспоненты р = d/dt.
Нетрудно проверить, что передаточная функция Ф(z) стационарной дискретной линейной системы, представляющей собой последовательное соединение ИЭ и непрерывной стационарной линейной системы, описываемой дифференциальные уравнением F(p)y=H(p)x, в случае простых корней р₁,...,р_n полинома F(p) определяется формулой

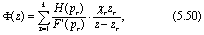
где z_r = 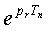, (r=1,2,...,k), η(τ)-функция
определяющая форму импульсов, вырабатываемых ИЭ.
Если F(p) имеет кратные корни, то выражение (5.50)
усложняется, но по-прежнему будет дробно-рациональной функцией переменной z. Приводя дроби в (5.50) или в аналогичной формуле для случая кратных корней полинома F(p) к общему знаменателю, получим передаточную функцию в виде отношения двух полиномов (5.48), по которому можно легко написать соответствующее разностное уравнение. Следовательно, математической моделью рассматриваемого соединения ИЭ и стационарной линейной системы, описываемой дифференциальным уравнением, является некоторое разностное уравнение которое легко находится по дифференциальному уравнению HЧ системы и функции η(t), определяющей форму импульсов, вырабатываемых ИЭ.
Изложенные выше математические модели дискретных САУ характерны тем, что они являются моделями типа "вход - выход" и учитывают особенности механизма квантования по времени. Математические модели дискретных САУ в пространстве состояний рассмотрим на примере цифровых САУ, но по-прежнему без учета особенностей квантования по уровню. Исследование цифровых САУ показывает, что квантованный по уровню сигнал можно представить как неквантованный сигнал с наложенной на него ошибкой квантования, изменяющейся в пределах ±T_n/2. При достаточно малом шаге квантования оно эквивалентно источнику шума на входе приведенной НЧ САУ и может быть учтено при исследовании точности системы, а при достаточно большом шаге квантования цифровая САУ должна исследоваться как существенно нелинейная релейная САУ. При этом могут использоваться методы, изложенные в разделе 4.