Математическое описание дискретных систем

Дискретная система может быть описана как с помощью внешних, так и внутренних математических моделей. Внешние модели являются моделями типа "вход - выход" и выражают зависимость только между выходом и входом системы, а внутренние модели, в частности модели пространства состояний описывают все внутренние связи между переменными системы.
Рассмотрим вначале дискретные (импульсные) линейные САУ и покажем, что для их описания могут использоваться дискретные аналоги временных (переходных), передаточных и частотных функций, рассмотренные в подразделе 2.1. Уточнение в скобках типа дискретной САУ означает, что главным в механизме квантования является квантование по времени, а особенности преобразования полученных дискретных значений не рассматриваются.

Рассмотрим случай, когда НЧ САУ является нестационарной линейной системой. Обозначим через w_k(t) реакцию дискретной линейной системы на кратковременное входное возмущение, равное единице и действующее только в течение времени действия k -го импульса. Тогда ее реакция на кратковременное возмущение, равное x(t_k) и действующее только в течение времени действия k-го импульса, будет на основании принципа суперпозиции равна w_k(f)x(t_k).
Реакция дискретной линейной системы на всю последовательность импульсов, модулированных входным возмущением x(t) , в силу принципа суперпозиции определится формулой
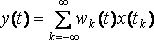(5.1)
Это основная формула, определяющая зависимость выходной переменной дискретной нестационарной линейной САУ от входного сигнала.
Функции w_k(t) определяют долю, или удельный вес, значений входной переменной, действующих в различные моменты времени t_k, в формировании выходной переменной системы в любой момент времени t. Поэтому функции w_k(t) называются весовыми коэффициентами дискретной линейной системы.
Весовые коэффициенты w_k(t) полностью характеризуют дискретную линейную систему, так как, зная эти функции, можно вычислить реакцию дискретной линейной системы на любое входное возмущение x(t).
Для физически возможной дискретной линейной системы, находящейся в покое до момента t₀ формула (5.1) примет следующий вид:
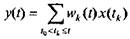(5.2)
где неравенство под знаком суммы означает, что суммирование распространяется только на моменты действия импульсов t_kє[t₀, t].
Если положить в (5.1) x(t)= δ(t - τ), то получим формулу для весовой (импульсной переходной) функции w(t,τ) дискретной линейной системы:
(5.3)
Следовательно, весовая функция любой дискретной линейной системы представляет собой линейную комбинацию δ - функций, и наоборот.
Конкретизируем описание дискретной линейной системы: пусть НЧ представляет собой непрерывную линейную систему с весовой функцией w₁(t,τ) (рис. 5.7), а ИЭ осуществляет АИМ.

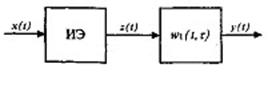
Рис. 5.7 - Импульсная САУ

Обозначим функцию, описывающую форму импульсов, вырабатываемых ИЭ, через η(t) (рис. 5.8). Тогда выходной АИМ - сигнал линейного ИЭ выразится формулой

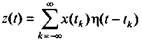
Эта функция является входной переменной непрерывной линейной системы с весовой функцией w₁(t,τ), следовательно,

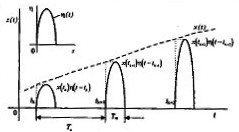
Рис. 5.8 - Выходной сигнал ИЭ

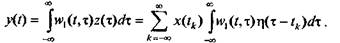
Поскольку 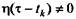только для , то

Из сравнения этой формулы с (5.1) следует, что

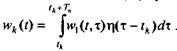
Вводя переменную 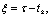получим
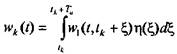(5.4)
Отсюда следует, что весовые коэффициенты последовательного соединения ИЭ и непрерывной линейной системы зависят от формы импульсов, вырабатываемых ИЭ, и весовой функции НЧ системы. Из (5.4) видно, что практически для любой физически возможной дискретной линейной системы начальные значения весовых коэффициентов w_k(t_k) = 0, поскольку при t = t_k подинтегральная функция тождественно равна нулю в интервале интегрирования (так как по определению w_k(t) = 0, при t < t_k) Для физически возможной дискретной системы w_k(t_k) могут быть отличны от нуля в теоретическом случае идеализированного ИЭ, вырабатывающего без запаздывания импульсы:
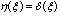если при этом
Пример 5.1. Найти весовые коэффициенты дискретной линейной системы, представляющей собой последовательное соединение ИЭ, вырабатывающего единичные прямоугольные импульсы длительностью Т_u, и апериодического звена.
Подставляя в (5.4) выражение весовой функции апериодического звена 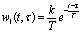и принимая во внимание, что 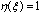при 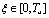, получим
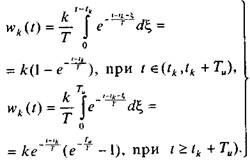(5.5)
На этом примере легко проверить, что w_k(t_k) =0.
Рассмотрим дискретную систему с ШИМ, при этом будем для простоты считать, что ИЭ (см. рис. 5.7) вырабатывает прямоугольные импульсы постоянной величины а, длительность которых пропорциональна значениям входного сигнала в соответствующие моменты времени. Тогда на вход НЧ поступают сигналы z(t) = a для моментов времени tє[t_k,t_k + χx(t_k)] и z=0 вне этого интервала. Согласно (2.10), получим
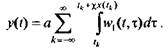(5.6)
Очевидно, что система, описываемая формулой (5.6), нелинейна. Однако при малой длительности импульсов ее можно приближенно рассматривать как линейную, так как в этом случае (5.6) перепишется в виде

Отсюда следует, что при ШИМ с кратковременными прямоугольными импульсами последовательное соединение ИЭ и непрерывной системы с весовой функцией w₁(t,τ) является линейной дискретной системой, весовые коэффициенты которой определяются соотношением
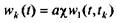. (5.7)
Величина аχ определяет интенсивность импульсов.
Аналогичные выкладки позволяют сделать вывод о том, что при ВИМ с импульсами произвольной формы последовательное соединение ИЭ и непрерывной линейной системы является линейной дискретной системой лишь при условии, что максимальный возможный временной сдвиг импульса настолько мал, что весовую функцию НЧ системы w₁(t,τ) можно приблизительно считать линейной функцией τ в диапазоне возможных значений временного сдвига.
Во многих случаях выходная переменная дискретной линейной системы интересует нас лишь в определенные моменты времени t'_l(l=0,±1,±2,...), или система выдает выходную переменную только в определенные моменты времени t'_l. Полагая в (5.1) t = t'_l, получим
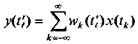(5.8)
Обозначая для краткости записи формулы (5.8) x_k=x(t_k), 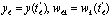, получим
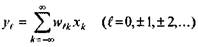(5.9)
Для случая, когда последовательность моментов фиксации выходной системы совпадает с последовательностью моментов действия импульсов t'_l = t_l, формула (5.2) при t = t_l определяет следующее выражение для выходной переменной физически возможной дискретной линейной системы:
(5.10)
Формулы вида (5.10) описывают, в частности, работу ЭВМ, когда результаты вычислений линейно зависят от исходных данных В этом случае исходные данные для линейной программы вычислений на ЭВМ, вводимые на каждом шаге вычислений, являются входными сигналами, а результаты вычислений на ЭВМ - выходными переменными.
Весовые коэффициенты ω_lk определяют линейную программу вычислений. Т.е. формула (5.10) на простейшем примере показывает, что динамические характеристики ЭВМ полностью определяются программой вычислений, т.е. решаемой задачей.
Перейдем к рассмотрению частного случая, когда НЧ САУ является стационарной линейной системой.
Известно, что стационарной называется такая система, реакция которой на любой данный тип возмущения зависит только от интервала времени между данным моментом времени и моментом начала действия возмущения.
С помощью рис. 5.2, а нетрудно убедиться в том, что дискретная система не может быть стационарной в смысле данного определения. Легко проверить, что при сдвиге входного возмущения во времени на величину, не равную целому числу периодов повторения (пунктирная кривая 2), значения входного возмущения x(t), действующего на систему, изменяются и вследствие этого выходной сигнал системы не только сдвигается во времени, но и изменяет свою форму.
Но если пренебречь интервалами времени, меньшими периода повторяемости импульсов Т, то можно определить стационарную и нестационарную дискретную систему.
Дискретную систему назовем стационарной, если при сдвиге во времени входного возмущения без изменения его формы на интервал времени, кратный периоду повторения импульсов, выходная переменная сдвигается во времени на такой же интервал без изменения своей формы, т.е. дискретная система может быть стационарной только тогда, когда действующие на систему входные возмущения следуют друг за другом через равные про, межутки времени. По определению весовой коэффициент w_k(t) линейной дискретной системы есть ее реакция на кратковременное возмущение (т.е. его длительность меньше Т), равное единице в момент времени t_k = kT_n.
Если система стационарна, то при сдвиге кратковременного единичного возмущения во времени на интервал iT_n ее реакция сдвинется во времени на тот же интервал iT_n, не изменяя формы, т.е. будет равна w_k(t-iT_n) .
С другой стороны, реакция системы на единичное возмущение, действующее в момент t_k+i=(k + i)T , равна ее весовому коэффициенту w_k+i(t).
Следовательно, для стационарной дискретной линейной системы при любых i и k справедливо равенство
w_k+i = w_k(t-iT_n).
Полагая k = 0, получим при любом i
w_i(t) = w₀(t-iT_n) (i = 0,±1,±2,...), (5.11)
т.е. весовые коэффициенты стационарной дискретной линейной системы представляют собой одну и ту же функцию, сдвинутую во времени на интервалы, кратные периоду повторения
импульсов.
В частности, для последовательного соединения ИЭ, вырабатывающего последовательность равноотстоящих импульсов, и стационарной непрерывной линейной системы с весовой функцией w(t-τ) из формулы (5.4) получим
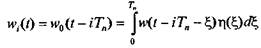(5.12)
Полагая в (5.12) t = t_l = lТ_n, получим
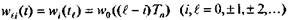, (5.13)
т.е. для стационарной дискретной линейной системы весовые коэффициенты w_li зависят только от разности индексов.
Обозначая разность индексов m, т.е. l - i = m, введем для весовых коэффициентов обозначение w_m. Для физически возможных стационарных дискретных линейных систем w(t) = 0 при t < 0, следовательно, w_m = 0 при m < 0. На основании изложенного выше для нестационарных реальных дискретных линейных систем и w₀ = 0.
Итак, весовые коэффициенты w_m последовательного соединения ИЭ и непрерывной стационарной линейной системы определяются формулой
. (5.14)
Формула (5.9) для стационарной дискретной линейной системы принимает вид
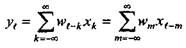.(5.15)