Передаточная функция стационарной дискретной импульсной линейной системы с дискретным выходом

Рассмотрим действие на стационарную дискретную линейную систему показательного возмущения х = e^pt. В этом случае 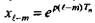, и из формулы (5.15) следует

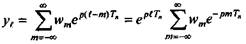
т.е. реакция стационарной дискретной линейной системы на показательное возмущение e^pt в момент t = lT равна значению этого же возмущения в тот же момент, умноженному на функцию
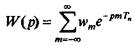(5.16)
зависящую только от комплексного параметра р. Функция W(p) является передаточной функцией стационарной дискретной линейной системы. Полагая в (5.16) р = iw, получим
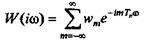(5.17)
Выражение (5.17) определяет частотную характеристику стационарной дискретной линейной системы в виде ряда Фурье. Коэффициентами этого ряда являются весовые коэффициенты системы.
Используя известную формулу для коэффициентов ряда Фурье, выразим весовые коэффициенты стационарной дискретной линейной системы через ее частотную характеристику
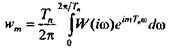(5.18)
Для физически возможной стационарной дискретной линейной системы получим
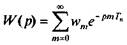(5.19)
Из формул (5.16) и (5.19) следует, что передаточные функции стационарных дискретных линейных систем являются функциями величины z = .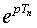
Обозначим через Ф(z) передаточную функцию физически возможной стационарной дискретной линейной системы, рассматриваемую как функцию параметра z, тогда
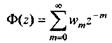(5.20)
Справедливы тождества
W(р)≡ Ф( 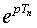); Ф(z) ≡ W((1/T_n)lnz). (5.21)
Формула (5.19) может быть получена из общей формулы (2.31), если заменить в ней функцию w(τ) линейной комбинацией δ-функций:

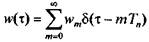
Это соотношение следует из (5.3). Следовательно, и для стационарной дискретной линейной системы передаточная функция является преобразованием Лапласа ее весовой (импульсной переходной) функции, которое в данном случае называется дискретным преобразованием Лапласа числовой последовательности
{w_m = {w(mT_n)} = {w[(l - i)T_n} = {w_i(t_l)} .
Функция (5.20) называется z-преобразованием последовательности величин {w_m}, а функция (5.19) является частным случаем z-преобразования.
Подобно тому как для анализа непрерывных линейных САУ удобно использовать преобразования Лапласа, для импульсных систем оказывается полезном z-преобразование и его частные случаи - дискретное преобразование Лапласа и дискретный аналог преобразования Фурье (см.(5.17)). Для выполнения этих преобразований используются теоремы и таблицы, представляющие собой дискретные аналоги табл.3.1.
Некоторые свойства z-преобразования приведены в табл.5.1.
Пример 5.2. Найти передаточную функцию замкнутой дискретной системы (рис.5.9), ИЭ которой вырабатывает прямоугольные импульсы длительностью Т_u с периодом повторения Т.

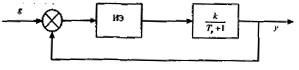
Рис. 5.9 - Пример дискретнй САУ

Найдем передаточную функцию разомкнутой системы. Подставляя в (5.20) выражения (5.5) для весовых коэффициентов разомкнутой импульсной системы, получим
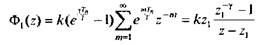(5.22)
Подставляя (5.22) в (2.58), определим передаточную функцию замкнутой системы

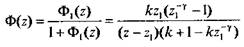
Наличие в импульсной системе инерционной НЧ приводит к тому, что на ее выходе процесс будет уже не дискретным, а непрерывным. Для определения значений выходных переменных в такой системе в промежутке между импульсами удобно использовать формулу t=n_n+εT_n (0≤ε<1).

Таблица 5.1 - Некоторые свойства z-преобразования

Подставляя это выражение в формулу (5.1) и вводя обозначения
y(nT_n+εT_n)=y_n(ε), (5.23)
w_k(nT_n+εT_n)=w₀((n-k)T_n+εT_n)=w_n-k(ε) (5.24)
получим для физически возможной стационарной дискретной линейной системы

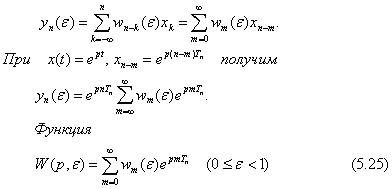
называется передаточной функцией стационарной дискретной линейной системы с непрерывным выходом.
При p = iω формула (5.25) определяет частотную характеристику стационарной дискретной линейной системы с непрерывным выходом. Наличие в аргументе этой функции ε отражает тот факт, что дискретная система может быть стационарной в полном смысле, т.е. по отношению к любым сдвигам во времени.
На основании (5.24) w_m(0)=w₀(тT_n)=w_m, поэтому при ε = 0 (5.25) совпадает с (5.19), т.е.
W(p,0) ≡ W(p). (5.26)
Рассматривая (5.25) как функцию параметра z = 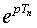, перепишем формулу (5.25) в виде
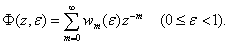(5.27)
Функция (5.27) называется модифицированным z-преобразованием последовательности величин (5.24), а по аналогии (5.25) - модифицированным дискретным преобразованием Лапласа.