ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
| 6.1 Общие сведения об оптимальном управлении и задачи синтеза оптимальных САУ |
В инженерной практике и, в частности, в ТАУ нередко возникают задачи о нахождении в некотором смысле наивыгоднейшего (оптимального) режима работы того или иного устройства. С математической точки зрения в таких задачах обычно требуется найти экстремум (максимум или минимум) некоторой величины при каких-нибудь ограничениях.
Включению в число экстремальных широкого круга задач управления способствовали работы А.А. Фельдбаума (1953г.), посвященные исследованию быстродействия САУ. А.А. Фельд-баум первый понял общий характер данной задачи управления и поставил вопрос о ее решении перед математиками (Л.С. Пон-трягиным и др.). Работы Л.С. Понтрягина и его учеников сыграли выдающуюся роль в развитии теории оптимального управления. Сформулированное ими решение задачи оптимального управления получило во всем мире название принципа максимума Понтрягина.
Независимо от русских работ в США Р. Беллман разработал свой метод решения задач управления в вариационной постановке, получивший название метода динамического программирования.
Вариационная постановка задачи управления вызвала огромное число публикаций разных авторов во многих странах мира, но среди них необходимо выделить нашего соотечественника Л.И. Розоноэра, который первым опубликовал в 1959 г. доказательство принципа максимума Понтрягина и обратил внимание на аналогию между принципом максимума Понтрягина и динамическим программированием Беллмана, с одной стороны, и между уравнениями Гамильтона и уравнениями Га-мильтона-Якоби классической механики, с другой стороны. В настоящее время теория оптимального управления и оптимизационная идеология проникли во многие научные исследования и конструкторские разработки, и без преувеличения можно сказать, что язык теории оптимального управления стал общим языком современной теории автоматического управления (СТАУ).
Итак, из вышеизложенного следует, что оптимальными САУ называются САУ, наилучшие в том или ином смысле. Эти системы могут быть как с обратными связями, так и без них (рис. 6.1, а, б).
На этом рисунке использованы обозначения рис. 1.5: g - задающее воздействие; u - управление; f1, f2, f3- возмущения, действующие на систему; К1, К2, К3 - операторы, определяющие преобразование функций g, u, у совместно с возмущениями в каналах связи системы.
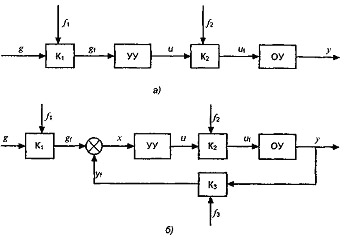
Рис. 6.1 - Структурные схемы оптимальных САУ
Синтез оптимальных САУ включает в себя следующие задачи:
- определение математической модели ОУ, т.е. определение функциональной зависимости выходной величины у от входного воздействия на объект uf, которая может быть задана различными способами, и в частности системой дифференциальных уравнений;
- оценку ограничений, как внутренних, присущих физическим процессам в ОУ, так и внешних, наложенных искусственно;
- определение желаемого поведения ОУ;
- задание определенной цели управления и выбор в соответствии с этой целью критерия оптимальности, характеризующего эффективность управления;
- определение стратегии УУ, т.е. такого алгоритма его работы, который при указанных выше условиях обеспечивает экстремум критерия оптимальности, т.е. максимальную эффективность управления;
- схемную реализацию УУ в соответствии с найденным алгоритмом его работы.
Синтез оптимальных САУ имеет ряд особенностей по сравнению с синтезом других систем. Во-первых, его цель - создание САУ, в которых используются все их возможности для достижения экстремальных значений наиболее важных показателей качества управления при удовлетворении заданных требований к остальным показателям. Во-вторых, при синтезе оптимальных САУ энергетические, механические и другие ограничения учитываются как факторы, определяющие возможности САУ по реализации экстремальных значений заданных показателей качества управления. Экстремальное значение одного из показателей качества управления оптимальной САУ реализуется только в том случае, если управляющее воздействие на ОУ и некоторые его координаты достигают ограничения и остаются определенное время ограниченными в процессе отработки задающего воздействия на систему, т.е. при оптимизации одного из качеств (свойств) системы обычно накладываются ограничения на другие ее свойства. Например, может быть предъявлено требование максимальной точности системы при одновременном ограничении ее быстродействия, стоимости и веса. В-третьих, качество синтезируемой оптимальной САУ зависит от правильности выбора критерия оптимальности, характеризующего эффективность управления, а достижение экстремума этого критерия является целью управления. Обоснование выбора того или иного критерия оптимальности связано с конкретными технико-экономическими условиями работы САУ и в теории оптимального управления не рассматривается.
Любой критерий оптимальности есть аналитическая оценка оптимизируемого качества системы, зависящая от ее параметров, задающего g и возмущающих ff, f2, f3 воздействий на нее и управляющего воздействия и на ОУ.
Следовательно, критерий качества выражается в виде функционала I(u), зависящего от функции управления u, а оптимальное управление u* определяется как функция, реализующая экстремум критерия качества, т.е. функционала I(u). Например, если к системе (см. рис. 6.1, б) предъявляется требование максимальной точности при условии f1 = f3 = 0, то критерием оптимальности может служить интеграл
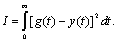 (6.1)
(6.1)
Так как выходная величина объекта y(t) связана с возмущением f2 и управлением u(t) зависимостью, определяемой системой дифференциальных уравнений объекта, то формула (6.1) может быть записана в следующем виде:
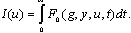
Минимальная ошибка будет в САУ, УУ которой формирует управление u*, при котором выполняется равенство
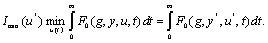
Такое управление называется оптимальным. Отклонение критерия I(u) от экстремального значения может служить мерой ухудшения качества системы.
Обычно ставится задача достижения экстремума одного функционала, но при этом могут накладываться дополнительные условия и ограничения на любые другие функции и функционалы. Например, можно потребовать выбора такого управления и, чтобы функционал I1(u) достигал минимума, а другие два функционала I1(u) и I1(u) не отклонялись от своих экстремумов более чем на ε2 и ε3 соответственно. Оптимальная САУ решает задачу достижения экстремума одного критерия оптимальности, однако принятый в качестве этого критерия функционал может представлять любую желаемую комбинацию оценок различных качеств синтезируемой системы, следовательно, в таком случае оптимизироваться будет не одно качество, а определенная их совокупность. Как правило, критерии оптимальности строятся так, чтобы цель управления достигалась при достижении минимума критерия.
Задачи синтеза оптимальных систем делятся на два класса:
1) оптимизация программы управления, или определение оптимального управления u(t) как функции времени, переводящего ОУ из начального состояния в заданное и реализующего минимум критерия качества, т.е. определение алгоритма УУ системы, схема которой приведена на рис. 6.1, а;
2) определение закона управления как функции фазовых координат ОУ u(у), обеспечивающего движение ОУ по фазовой траектории, на которой реализуется минимум критерия оптимальности, т.е. определение алгоритма УУ замкнутой системы, схема которой приведена на рис. 6.1, б.
Первый класс задач чаще всего используется как первый этап решения задач второго класса. Частным случаем второго класса задач является задача аналитического конструирования регуляторов. Такое название получила методика определения алгоритма УУ в замкнутой системе, схема которой приведена на рис. 6.1, б, при условии, что возмущения f1 и f3 отсутствуют, а возмущение f2, представляет собой последовательность скачкообразных функций времени, ограниченных по модулю, |f2k(t)| ≤ N = const (k=l,2,...,r).
УУ должно обеспечивать оптимальные показатели качества переходного процесса при ликвидации отклонений изображающей точки ОУ от программной траектории при заданных ограничениях на управление.
В настоящее время существует несколько направлений классификации оптимальных систем. При классификации по оптимизируемым показателям качества САУ различают следующие типы систем:
- оптимальные по быстродействию;
- оптимальные по расходу ресурсов;
- с минимальной энергией управления;
- с минимальными потерями управления.
При определении принципа действия перечисленных типов систем целесообразно использовать понятие n-мерного пространства состояний (фазового пространства), в качестве координат которого выбираются п линейно независимых функций, полностью определяющих изменение состояния системы во времени. В частности, это могут быть функции, относительно которых записывается нормальная система дифференциальных уравнений ОУ. Тогда состояние системы в каждый момент времени будет определяться точкой в ее фазовом пространстве, а изменение состояния системы характеризуется траекторией ее изображающей точки.
Используя понятие фазового пространства, можно дать определения указанных выше типов оптимальных систем в наиболее компактной форме.
Оптимальными по быстродействию называют системы, УУ которых формирует такое допустимое управление u(t) , которое переводит в фазовом пространстве изображающую точку ОУ из одного заданного состояния y(t0) в другое у(Т) за минимальное время T-t0.
Системы, оптимальные по расходу ресурсов, переводят в фазовом пространстве изображающую точку ОУ из начального состояния в заданную область V с минимальными затратами ресурсов (топлива, катализатора и т.п.).
Системами с минимальной энергией управления называют системы, которые при переводе изображающей точки ОУ из начального положения в заданное обеспечивают минимум функционала 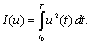
Системы с минимальными потерями управления, переводя изображающую точку ОУ из начального состояния в заданное, минимизируют отклонение действительных координат объекта от предписанных значений. К этому типу систем, в частности, относятся следящие системы с минимальными ошибками воспроизведения задающего воздействия.
Вторым направлением классификации оптимальных систем является классификация по характеристикам ОУ. Системы делятся на непрерывные, дискретно-непрерывные и дискретные.
В непрерывных системах координаты ОУ и воздействия на него не квантованы ни по времени, ни по уровню. В дискретно-непрерывных системах эти величины квантованы по времени, а в дискретных - и по времени, и по уровню.
Различают оптимальные системы и по типам дифференциальных уравнений ОУ и делят их на системы с линейными, нелинейными объектами и объектами с распределенными параметрами, динамика которых описывается дифференциальными уравнениями в частных производных.
Важными характеристиками ОУ являются ограничения, накладываемые на управление u(t), на его координаты и на возмущения, действующие на него. Поэтому при определении классов оптимальных систем различают:
- системы с ограничением на управление, когда в системе должны выполняться неравенства
|u1| ≤ M1, |u2| ≤ M2,… , |um| ≤ Mm, (6.2)
где М1, М2,..., Мm - заданные константы;
- системы с ограничениями на координаты ОУ и с ограничениями на возмущения; ограничения на координаты и возмущения могут накладываться как в виде неравенств (6.2), так и в виде ограничений на функционалы координат и возмущений.
Третьим направлением классификации оптимальных систем является классификация по характеру критерия оптимальности. При этом различают следующие типы систем: равномерно - оптимальные; статистически - оптимальные; минимаксно - оптимальные.
К первому типу относятся такие системы, процессы в которых в каждом отдельном случае являются оптимальными. Например, равномерно-оптимальная по расходу топлива система ориентации космического корабля будет переводить его из любого произвольного положения в заданное с минимальным расходом топлива.
Системы второго типа оптимальны не в каждом отдельном случае, а в среднем, т.е. они дадут наилучший средний результат по сравнению с неоптимальными системами при большом количестве опытов. Критерий оптимальности этого типа систем имеет статистический характер. К ним относятся системы, на процессы в которых так или иначе влияют случайные факторы.
Минимаксно-оптимальные системы обеспечивают наилучший по сравнению с неоптимальными САУ результат только в наихудшем случае, т.е. наихудший результат в такой системе лучше, чем наихудший результат в неоптимальной системе.
Для определения алгоритма работы УУ оптимальной системы необходимо, чтобы это устройство имело следующую информацию об ОУ (см. рис. 6.1):
- об операторе ОУ, т.е. о зависимости у = F(u,f2);
- о возмущении f1, действующем на ОУ;
- о состоянии ОУ, или информацию о его фазовых координатах (переменных состояния);
- о критерии оптимальности;
- о задающем воздействии g.
В зависимости от полноты и характера информации, поступающей на УУ, оптимальные системы делятся на три типа:
1) оптимальные системы с полной или максимально возможной информацией об ОУ;
2) оптимальные системы с неполной информацией об ОУ и независимым (пассивным) ее накоплением в процессе управления;
3) оптимальные системы с неполной информацией об ОУ и активным ее накоплением в процессе управления. При этом предполагается, что в УУ всех трех типов систем раложена полная информация об операторе объекта и о критерии оптимальности.
Если кроме этого в УУ имеется полная информация о задающем воздействии g(t) (см. рис. 6.1), о возмущении f2, приложенном к ОУ, и полная текущая информация о состоянии у ОУ в данный момент времени t, а возмущения f1 и f3 отсутствуют, то такая оптимальная система принадлежит к первому типу.
Полная информация о задающем воздействии означает полные сведения о поведении этой функции в прошлом, настоящем и будущем, т.е. знание зависимости, позволяющей получить ее значения в любой момент времени.
Полная информация о текущих значениях фазовых координат позволяет определить все поведение объекта в будущем. Очевидно, на практике в большинстве случаев информацию об ОУ нельзя считать полной.
Отсутствие полной информации об ОУ, задающих и возмущающих воздействиях вынуждает рассматривать системы второго и третьего типов.
В системах второго типа в УУ используется информация не о самих воздействиях, а лишь статистические характеристики случайных задающих воздействий и случайных возмущений, действующих на объект. Структурная схема оптимальной системы в этом случае может иметь вид, изображенный на рис. 6.1, а и б, при условии, что f3=0, а помеха f2 аддитивно смешивается с воздействиями на объект. Для выбора оптимального алгоритма УУ необходимо знание максимально возможной информации о задающих воздействиях и возмущениях.
Накопление этой информации в системах второго типа осуществляется путем наблюдения и не зависит от алгоритма УУ. Накопленная информация используется для построения гипотез о воздействиях на объект и для перестройки в соответствии с этими гипотезами параметров УУ.
К системам третьего типа относятся системы со структурной схемой, представленной на рис. 6.1, б. В них управление u(t) решает следующие задачи:
- осуществляет такое изменение состояния объекта, при котором происходит накопление максимума информации о неизвестных характеристиках объекта, воздействиях и возмущениях;
- переводит ОУ из начального состояния в заданное по фазовой траектории, на которой реализуется минимум критерия оптимальности.
В связи с двойственным характером управление в системах третьего типа называется дуальным. Системы второго и третьего типов называют также оптимальными системами с адаптацией, так как в них в процессе управления осуществляется изучение условий работы системы, накопление информации об этих условиях, изменение закона управления на основании полученной информации, и, таким образом, эти системы приближаются к системам с полной информацией.
Практическая реализация оптимальных систем со сложными ОУ требует применения в УУ вычислительных устройств, выполняющих расчетные и логические операции. Для упрощения решения задач синтеза подобных САУ целесообразно использовать квазиоптимальные системы управления.
Квазиоптимальными или субоптимальными (близкими к оптимальным) называют САУ, алгоритм УУ которых получен путем сравнительно небольших отступлений от оптимального алгоритма. При этом УУ таких САУ может реализоваться по достаточно простой схеме без сложных вычислительных устройств.
Задача синтеза оптимальных САУ, а точнее, задача определения алгоритма УУ САУ относится к классу вариационных задач, для решения которых наиболее широко используются следующие методы:
- классического вариационного исчисления;
- принципа максимума Понтрягина;
- динамического программирования;
- Винера - Колмогорова и Калмана - Бьюси;
- оптимизации критерия обобщенной работы;
- функционального анализа;
- метрического анализа.
Далее рассматриваются первые три метода решения вариационных задач оптимального управления с полной информацией, а также оптимальные системы с неполной информацией (с адаптацией).
| 6.2 Вариационное исчисление и его использование в теории оптимальных САУ |
Методы вариационного исчисления позволяют найти условия, при которых достигается экстремум критерия оптимальности, записанного в виде некоторого функционала. Условия получаются в виде некоторой системы уравнений относительно управления и переменных состояния ОУ (фазовых координат объекта). Решение этой системы, удовлетворяющее граничным условиям, определяет оптимальное управление и оптимальную траекторию изображающей точки ОУ в его пространстве состояний. При записи условий существования экстремума функционала используются следующие понятия и определения.
1. Функционал - переменная величина I, зависящая от функций
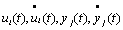 (i = l,2,...,m; j = 1,2,...,n) . (6.3)
(i = l,2,...,m; j = 1,2,...,n) . (6.3)
При этом каждой из функций (6.3), взятой из некоторого класса этих функций, соответствует определенное значение функционала I, что записывается в виде
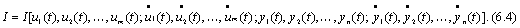
2. Приращение, или вариация, δui, аргумента ui(t) функционала (6.4) есть разность функций
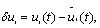
где  - новая произвольно выбранная функция из класса функций ui(t).
- новая произвольно выбранная функция из класса функций ui(t).
3. Близость двух функций характеризуется определенным порядком близости.
Например, функции u1(t) и  близки в смысле близости нулевого порядка, если модуль разности u1(t) -
близки в смысле близости нулевого порядка, если модуль разности u1(t) -  мал (рис. 6.2, а); функции u2(t) и
мал (рис. 6.2, а); функции u2(t) и 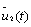 близки в смысле близости первого порядка, если модули разностей u2(t) -
близки в смысле близости первого порядка, если модули разностей u2(t) - 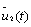 и
и 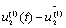 малы (рис. 6.2, б).
малы (рис. 6.2, б).
4. Функционал (6.4) называется непрерывным при 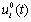 в смысле близости k-гo порядка, если для любого положительного ε можно подобрать такое δ > 0, что
в смысле близости k-гo порядка, если для любого положительного ε можно подобрать такое δ > 0, что
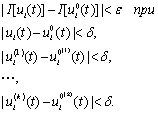
Функции ui(t) берутся из класса функций, на котором функционал (6.4) определен.
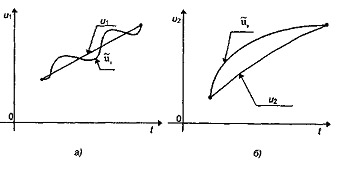
Рис. 6.2 - Функции нулевого и первого порядков близости
5. Приращение функционала (6.4), соответствующее вариациям аргументов
определяется в виде
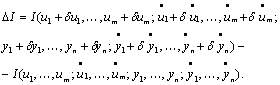 (6.5)
(6.5)
Если функционал (6.4) имеет в некоторой области непрерывные частные производные второго порядка, то его приращение (6.5) может быть разложено в ряд Тейлора:

Представление приращения функционала (6.4) в форме (6.6) позволяет достаточно просто определить его вариации.
6. Если приращение функционала ∆I может быть представлено рядом Тейлора (6.6), то линейная по отношению к вариациям аргументов часть приращения функционала называется первой вариацией функционала и записывается в виде
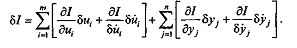
7. Второй вариацией функционала (6.4) называется функция
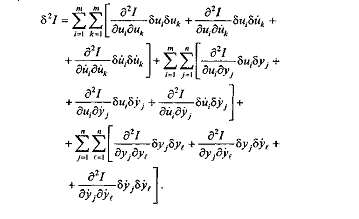
Необходимым условием существования экстремума непрерывного функционала является равенство нулю его первой вариации:
δI=0. (6.7)
Если достигается минимум функционала, то выполнение условия (6.7) должно сопровождаться выполнением необходимого условия δ2I ≥ 0, а в случае достижения максимума - условия δ2I ≤ 0.
Приведенные необходимые условия существования экстремума функционала справедливы, если непрерывный функционал определен на открытом множестве функций, или если функционал определен на замкнутом множестве функций, то экстремум функционала реализуется функциями, не принадлежащими границе множества. Особенности определения необходимых условий существования экстремума функционала в случае, когда этот экстремум реализуется функциями, частично или полностью принадлежащими границе множества, на котором этот функционал определен, будут рассмотрены ниже.
В подавляющем большинстве случаев критерий оптимальности записывается в виде интеграла. В частности, он может быть записан так:
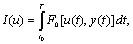 (6.8)
(6.8)
где 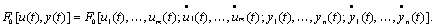
Если подынтегральная функция F0[u(t), y(t)] непрерывна по совокупности ее аргументов и существуют все ее частные производные до третьего порядка включительно, то необходимые условия экстремума функционала (6.8) записываются в виде системы дифференциальных уравнений Эйлера - Лагранжа:
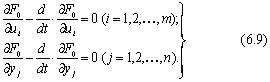
Условие (6.9) эквивалентно условию (6.7). Поэтому только на интегральных кривых уравнений Эйлера-Лагранока, удовлетворяющих граничным условиям
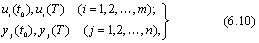
может реализоваться экстремум функционала (6.8).
Интегральные кривые уравнений Эйлера-Лагранжа называются экстремалями. Экстремали, удовлетворяющие граничным условиям, определяются путем решения краевой задачи. Следует помнить, что это решение не всегда существуем, а если и существует, то может быть не единственным. Однако во многих задачах синтеза оптимальных САУ из физического или геометрического смысла задачи достаточно просто устанавливается существование решения, его единственность и то, что оно реализует минимум критерия оптимальности. В этом случае экстремали, удовлетворяющие граничным условиям, есть решение оптимальной задачи.
Если же существует несколько решений уравнения (6.9), удовлетворяющих граничным условиям (6.10), то путем вычисления значений критерия оптимальности на каждом из полученных решений выбирается то из них, на котором критерий достигает минимума.
Экстремум функционала (6.8) может достигаться не на гладких, а на кусочно-гладких экстремалях с конечным числом угловых точек.
Угловыми точками называют точки, в которых экстремали непрерывны:
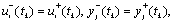
а производные от экстремалей терпят разрывы первого рода (рис. 6.3):
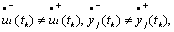
где 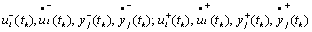 - соответственно, левые и правые пределы экстремалей и их производных в k-й угловой точке.
- соответственно, левые и правые пределы экстремалей и их производных в k-й угловой точке.
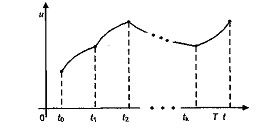
Рис. 6.3 - Экстремаль с угловыми точками
Если экстремум функционала реализуется на экстремалях с угловыми точками, которые называются ломаными экстремалями, то в каждой угловой точке должны выполняться условия Вейерштрасса - Эрдмана:

В теории оптимальных САУ возникают задачи, когда одна или обе граничные точки экстремалей перемещаются по определенному закону. Например, ракетой А (рис. 6.4) надо управлять так, чтобы уничтожить ракету В за минимальное время. Ракета А запускается с самолета. Очевидно, что в этом случае могут быть заданы только начальные условия (координаты ракет А и В, значения их скоростей, ускорений в момент старта) и не могут быть заданы граничные условия, т.е. указанные выше параметры в момент встречи двух ракет, так как последние зависят от искомого минимального времени Т* сближения ракет А и В.
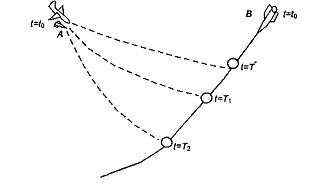
Рис 6.4 - Задача перехвата ракеты В ракетой А за минимальное время
Подобные задачи в вариационном исчислении называются задачами с подвижными концами или границами (выше рассматривалась задача с закрепленными концами). В таких задачах необходимые условия существования экстремума функционала (6.9) должны быть дополнены условиями:
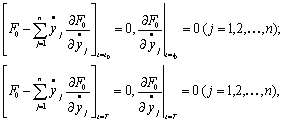
если не задан закон перемещения концевых точек,
 (6.11)
(6.11)
где  - закон перемещения концевой точки экстремали yj(t0);
- закон перемещения концевой точки экстремали yj(t0);
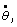 - закон перемещения концевой точки экстремали уj(Т).
- закон перемещения концевой точки экстремали уj(Т).
Условия (6.11) носят название условий трансверсальности.
В большинстве случаев при синтезе оптимальных САУ возникают задачи минимизации критерия оптимальности при дополнительных условиях, наложенных на координаты ОУ и на граничные условия. В классическом вариационном исчислении такие задачи получили название задач на условный экстремум.
Простейшая задача на условный экстремум формулируется так: требуется исследовать на экстремум функционал (6.8) при условии, что экстремали, на которых реализуется минимум функционала, должны удовлетворять системе дифференциальных уравнений
Fj(t, y1, y2, ..., yn) = 0 (у=1,2,..,n), (6.12)
которую называют системой уравнений связи. Эта задача решается путем преобразования функционала (6.8) к виду
 (6.13)
(6.13)
где 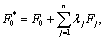
λj - неопределенные множители Лагранжа, и исследования нового функционала (6.13) на безусловный экстремум.
Необходимые условия существования безусловного экстремума функционала (6.13) и, следовательно, условного экстремума функционала (6.8) имеют вид
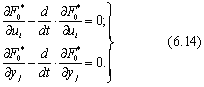
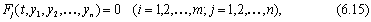
где (6.14) - система уравнений Эйлера - Лагранжа, (6.15) - система дифференциальных уравнений связи.
Условия (6.14) и (6.15) состоят из (2n+m) уравнений относительно (2n+m) неизвестных u1, ..., um; у1, ..., уn; ╏, ..., λn и, следовательно, позволяют определить эти неизвестные функции. Решения систем уравнений (6.14) и (6.15) будут содержать 2(2n+m) неизвестных постоянных интегрирования. С помощью 2(n+m) граничных условий, заданных для экстремалей ui(t) и yj(t) , можно определить 2(n+m) постоянных интегрирования. Остальные 2n постоянных интегрирования находятся путем подбора 2n незаданных граничных условий для множителей Лагранжа λj таким образом, чтобы удовлетворялись граничные условия для функций uj(t) и уj(t) .
Иногда при решении вариационных задач на условный экстремум возникает необходимость выбора из класса кусочно-гладких вектор-функций u(t), y(t) тех, которые доставляют экстремум функционалу
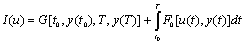
и удовлетворяют уравнениям связи (6.12) и условиям на концах
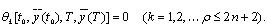
Такую задачу называют задачей Больца.
Применение методов классического вариационного исчисления для решения задач синтеза оптимальных САУ ограничено следующими трудностями.
Во-первых, в реальных системах допустимые управляющие воздействия принадлежат замкнутому множеству функций, т.е. удовлетворяют условиям вида (6.2), и чаще всего наилучшие результаты получаются в том случае, если оптимальные управления выбираются из числа функций, частично или полностью принадлежащих границе этого множества. Например, управляющее напряжение на входе оптимального по быстродействию электропривода, динамика которого описывается дифференциальным уравнением второго порядка, должно изменяться так, как это показано на рис. 6.5.

Рис. 6.5 - График изменения напряжения на выходе оптимального по быстродействию электропривода
При этом оказывается, что минимум критерия оптимальности, являющегося функционалом от управления u(t) , достигается при |u(t)| = М = const, хотя при этих условиях первая вариация функционала не равна нулю (рис. 6.6).
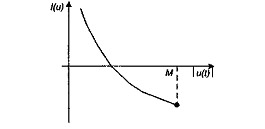
Рис. 6.6 - График зависимости величины функционала I(u) от модуля управления |u(t)|
Во-вторых, если оптимальное управление принадлежит к классу кусочно-постоянных функций с конечным числом точек разрывов первого рода (например, рис. 6.5), то это создает значительные вычислительные трудности при определении алгоритма УУ оптимальной САУ.
Первая из отмеченных выше трудностей преодолевается путем замены замкнутого множества допустимых управлений открытым. Такая замена может быть осуществлена, в частности с помощью "функций штрафа" или функций, предложенных Мьеле. При использовании "функций штрафа", в критерий оптимальности вводится дополнительная функция от управления, которая вызывает резкое увеличение критерия, если управление превышает допустимое значение, т.е. "штрафует" за "нарушение". Если на управление наложено ограничение
|u(t)| ≤ М = const, (6.16)
то "функция штрафа" может быть выбрана в виде
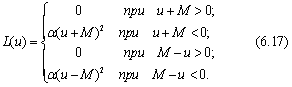
Используя функцию (6.17), можно методами классического вариационного исчисления определять условия существования минимума критерия оптимальности и в случае, когда оптимальное управление выбирается из замкнутого множества допустимых управлений.
При использовании функций Мьеле ограничение вида (6.16) учитывается с помощью замены управления u(t) функцией
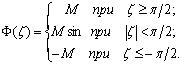 (6.18)
(6.18)
Изложим постановку задачи определения алгоритма УУ различных типов САУ на основе методов классического вариационного исчисления.
| 6.2.1 Системы, оптимальные по быстродействию |
Задана система дифференциальных уравнений, описывающая динамику ОУ:
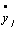 = Fj(y1, y2, ..., yn; u1, u2, ..., um) (j=1,2,...n), (6.19)
= Fj(y1, y2, ..., yn; u1, u2, ..., um) (j=1,2,...n), (6.19)
где yj - координаты ОУ; ui - управляющие воздействия.
На управляющие воздействия наложены ограничения
|u1| ≤ М1, |u2| ≤ М2, ..., |um| ≤ Мm, (6.20)
где М1, М2, ..., Мm - заданные константы.
Необходимо найти функции ui = ui(t) (в разомкнутой системе) или ui = ui(y1, y2, ..., yn) (в замкнутой системе), удовлетворяющие офаничениям (6.20), переводящие ОУ из начального состояния 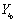 {y1(t0), ..., yn(t0)} в заданное YT{y1(T), ..., yn(T)} и обеспечивающие минимум функционала (критерия оптимальности)
{y1(t0), ..., yn(t0)} в заданное YT{y1(T), ..., yn(T)} и обеспечивающие минимум функционала (критерия оптимальности)
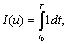 (6.21)
(6.21)
где Т- незаданное время перехода ОУ из состояния в состояние YT.
Минимум функционала (6.21) обеспечивается при минимальном времени перехода ОУ из начального состояния в заданное. Так как экстремали функционала (6.21) должны удовлетворять системе уравнений (6.19), то поставленная задача является вариационной задачей на условный экстремум функционала (6.21).
| 6.2.2 Системы, оптимальные по расходу ресурсов |
Такие САУ разрабатываются для управления различными типами ракет и управляемых космических аппаратов, а также для определения оптимальных режимов полета самолетов и режимов работы химических и металлургических промышленных установок.
Как и в предыдущей задаче, заданы система дифференциальных уравнений динамики ОУ (6.19), ограничение на управление (6.20) и граничные условия 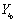 , YT. Кроме того, полагается известной связь скорости расхода топлива с управляющими воздействиями ui. Часто эта зависимость имеет вид
, YT. Кроме того, полагается известной связь скорости расхода топлива с управляющими воздействиями ui. Часто эта зависимость имеет вид
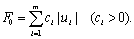
Тогда общее количество топлива I, израсходованного на временном интервале [t0, T], определяется функционалом
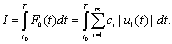 (6.22)
(6.22)
Как и в предыдущем случае, задача заключается в выборе из замкнутого множества функций (6.20) таких управляющих воздействий ui = ui(t) или ui = ui(y1, y2, ..., yn), которые переводят ОУ из начального состояния в заданное так, чтобы функционал (6.22) принимал минимальное значение. При этом время достижения конечного состояния Т может быть как неограниченным, так и ограниченным. Данная задача, как и предыдущая, является задачей на условный экстремум.
| 6.2.3 Системы, оптимальные по расходу ресурсов |
Постановка задачи синтеза таких систем не отличается от постановки предыдущей задачи, за исключением минимизируемого критерия оптимальности, который в этой задаче имеет вид
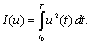
| 6.2.4 Системы с минимальными потерями управления |
Синтез таких систем получил название аналитического конструирования регуляторов. При решении этой задачи, как и ранее, полагается, что заданы система уравнений динамики ОУ (6.19), ограничения (6.20) и естественные граничные условия:
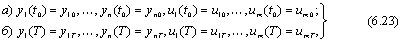
которые означают, что синтезируемое УУ, ликвидируя вызванное скачкообразным возмущающим воздействием отклонение изображающей точки ОУ от программной траектории g(t), должно обеспечить либо минимальное отклонение изображающей точки ОУ от программной траектории, либо возвращение на эту траекторию по окончании переходного процесса. В последнем случае граничные условия (6.23, б) запишутся в виде
y1(∞) = ... = yn(∞) = u1(∞) = ... um(∞) = 0 .
Системы с минимальными потерями управления решают задачу оптимальной отработки отклонений изображающей точки ОУ от программной траектории, поэтому при синтезе УУ можно положить задающее воздействие на систему g(t) (см.рис. 6.1, б)
равным нулю. Тогда составляющие вектора y(t) будут равны составляющим вектора ошибки системы z(t).
Задачей аналитического конструирования регуляторов является определение закона управления в форме дифференциального уравнения вида f(... 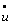 , u, y(t), t) = 0 , такого, чтобы УУ, присоединенное к ОУ, обеспечивало минимум функционала
, u, y(t), t) = 0 , такого, чтобы УУ, присоединенное к ОУ, обеспечивало минимум функционала
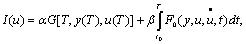 (6.24)
(6.24)
где 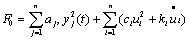 - положительно определенная квадратичная форма; G - функция, оптимизирующая конечное состояние системы и равная нулю при T = ∞ на всевозможных допустимых возмущенных движениях, возникающих в области определения уравнений (6.19) с учетом ограничений, наложенных на управление и координаты ОУ.
- положительно определенная квадратичная форма; G - функция, оптимизирующая конечное состояние системы и равная нулю при T = ∞ на всевозможных допустимых возмущенных движениях, возникающих в области определения уравнений (6.19) с учетом ограничений, наложенных на управление и координаты ОУ.
Критерий оптимальности (6.24) характеризует взвешенные по константам аi, сi, ki интегральную квадратичную ошибку и затраты энергии на управление, т.е. является интегральной квадратичной функцией потерь управления. При аналитическом конструировании регуляторов по-прежнему решается вариационная задача на условный экстремум. Определение алгоритма УУ, реализующего минимум функционала (6.24), имеет две особенности:
- во-первых, в результате решения систем уравнений (6.14) и (6.15), определяющих необходимые условия существования минимума функционала (6.24), находится дифференциальное уравнение физически нереализуемого оптимального УУ, так как его характеристическое уравнение имеет как отрицательные, так и положительные корни. Поэтому синтезируемое УУ реализуется по алгоритму, полученному из уравнения оптимального УУ путем отбрасывания в его решении экспоненциальных членов с положительными показателями;
- во-вторых, решение вариационной задачи позволяет определить закон управления, реа<
Дата добавления: 2021-04-21; просмотров: 1750;











