Гармонические коэффициенты усиления некоторых типовых нелинейных звеньев

Характеристики F(x) нелинейных звеньев делятся на две основные группы - однозначные и неоднозначные.
Рассмотрим для примера нелинейные звенья с однозначными характеристиками. Для таких звеньев q' ≡ 0, так как при гармоническом воздействии основная гармоника выходных колебаний нелинейных элементов совпадает по фазе с выходной величиной.
Ограничимся рассмотрением нелинейных звеньев с симметричной характеристикой относительно начала координат. Для таких характеристик F(x) - нечетная функция.
В качестве примера рассмотрим кусочно-линейную характеристику 1, показанную на рис. 1.11, в:

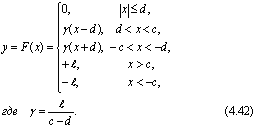
На характеристике у = F(x) можно указать три зоны:
1) зона нечувствительности |х| ≤ d;
2) зона линейности d < x < c;
3) зона насыщения |х| > |с|.
Прежде чем приступить к определению q, построим вспомогательный рис. 4.21. Кривая на рис.4.21 изображает изменение входной величины нелинейного звена х = asinωt = asinφ, а ломаная - изменение выходной величины у.

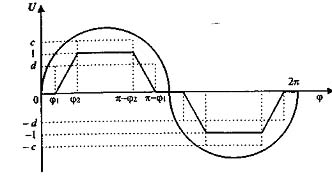
Рис. 4.21 - Расчет гармонических коэффициентов

От момента времени t = 0 до того момента, когда х станет равным d, выходная величина у = 0. В этот момент фазовый угол φ₁ определяется из равенства d = asinφ₁:
φ₁ = arcsin(d/a) (4.43)
Начиная с момента ωt₁ = φ₁ до момента ωt₂ = φ₂, где φ₂ определяется из равенства с = asinφ₂:
φ₂ = arcsin(c/a) (4.44)
выходная величина у линейно зависит от х:
у = γ(x - d) = γ(аsinφ - asinφ₁) = γа(sinφ - sinφ₁).
На участке φ₂ < φ < π - φ₂ выходная величина у = 1, а на участке π - φ₂ < φ < π - φ₁, опять зависит линейно от х.
Учитывая то, что в пределах 0 < φ < φ₁, подынтегральная Функция тождественно равна нулю, а также учитывая симметричность кривой у относительно прямых ωt = π/2 и ωt = 3π/2, выражение для q (см. (4.38)) представим в следующем виде:
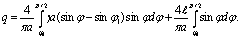(4.45)
Взяв интегралы и учитывая уравнения (4.42) - (4.44), получим:

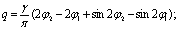
Из этой формулы вытекают следующие частные случаи:
а) имеет место насыщение, но зона нечувствительности отсутствует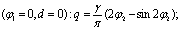
б) есть зона нечувствительности, но насыщение отсутствует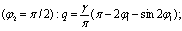
в) идеальное двухпозиционное реле (d = с = 0, φ₂ = φ₁ = 0), для которого первый интеграл в (4.45) исчезает и q = 4l/πа.
Если однозначная нелинейность несимметрична, то появляется постоянная составляющая.
В качестве примера рассмотрим идеальный выпрямитель, характеристика которого имеет вид:

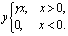
Если на вход действует гармоническое возмущение x=asinωt, то

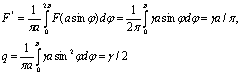
и первая гармоника выходного колебания равна:

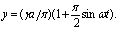
В данном случае несимметрия характеристик обусловлена физическими свойствами самого нелинейного звена. Другой причиной появления несимметричности характеристик нелинейного звена может быть наличие постоянной составляющей на входе:

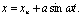
Если характеристика F(x) неоднозначна и образует петли, то выходное колебание сдвигается по фазе и появляется комплексная составляющая гармонического коэффициента передачи пропорциональная площади петли. В качестве примера нелинейного звена с неоднозначной характеристикой рассмотрим двухпозиционное реле с зоной нечувствительности (рис.4.22).

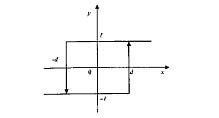
Рис. 4.22 - Рылейная характеристика с зоной нечувствительности

На входе звена действует сигнал: .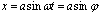
В этом случае F* = 0, а интеграл для вычисления коэффициента q должен быть записан в виде:

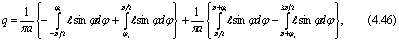
где первые два интеграла соответствуют ветви кривой функции F Для случая возрастания sinφ , вторые два интеграла соответствуют ветви кривой F для случая убывания sinφ,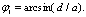
Вычислив интегралы (4.46), получим
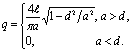(4.47)
Для коэффициента q' имеем:

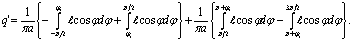
Вычислив эти интегралы, получим
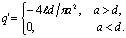(4.48)