Качество переходных процессов и коррекция нелинейных САУ

В нелинейных САУ качество переходных процессов принято оценивать теми же показателями, что и в линейных системах: временем переходного процесса t_п максимальным отклонением и колебательностью. Но в нелинейных САУ эти показатели зависят от величины внешнего воздействия, породившего переходный процесс.
Анализ показателей качества переходных процессов в нелинейных системах начнем с наиболее простого случая, когда предполагается, что входящие в систему нелинейности не оказывают существенного влияния на динамику системы. В этом случае в первом приближении можно исследовать качество переходных процессов и построить сам процесс без учета всех нелинейностей, т.е. исследовать систему как линейную. Такое исследование возможно, например, для непрерывных САУ с насыщением, небольшой зоной нечувствительности, неоднозначной характеристикой с достаточно узкой петлей и т.д. (см. пример в подразделе 4.2). После проведения приближенного исследования оценивается влияние на динамику САУ неучтенных нелинейностей. Если проводился приближенный синтез системы, то после этого при необходимости проводится дополнительная коррекция. Осуществляется также построение переходных процессов с учетом исключенных нелинейностей. Для этого используются методы численного интегрирования и ЭВМ.
Для приближенной оценки влияния нелинейностей используется метод гармонической линеаризации. Нелинейное звено заменяется гармонически линеаризованным звеном и предполагается, что его комплексный гармонический коэффициент усиления W_н(а) справедлив и для случая произвольной формы входного сигнала х. Формально это выражается заменой в W_н(a) величины а на x. Выразив таким образом параметры комплексного гармонического коэффициента усиления через входной сигнал х и определив зависимость качества переходных процессов в линейной системе от значений этих параметров, можно приближенно оценить влияние нелинейности звена на переходные процессы. Например, для звена с насыщением эта методика предлагает замену эквивалентным звеном, гармонический коэффициент передачи которого уменьшается с ростом входного сигнала х так же, как гармонический коэффициент передачи этого звена уменьшается с увеличением амплитуды а входных колебаний. Для оценки быстродействия в гармонически линеаризованной системе применяется показатель колебательности М и полоса пропускания. В отличие от линейных систем здесь вместо одной частотной характеристики строится серия таких характеристик в зависимости от амплитуды а. Соответственно и качество переходных процессов будет зависеть от величины отклонения от установившегося режима.
Для нелинейных систем второго порядка качество переходных процессов полностью определяется по фазовому портрету системы. Для нелинейных систем, устойчивость которых исследовалась с помощью второго (прямого) метода Ляпунова или критерия абсолютной устойчивости В.М. Попова длительность переходных процессов можно оценить с помощью этих же методов на основе понятия степени устойчивости η (см. подраздел 3.4).
Предположим, что у нас есть возможность определить максимальное значение η, при котором для всех возможных процессов x(t) в нелинейной системе выражение х(t)е^ηt ⊾ 0 при t ⊾ ∞, а при бесконечно малом превышении этого значения η это условие уже не выполняется. Это значит, что переходные процессы в системе затухают не медленнее, чем экспонента e^-ηt. Следовательно, найденная величина ηt может служить оценкой сверху длительности t_п переходных процессов в системе, т.е. .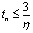
Так как в линейной системе переходный процесс может быть представлен в виде суммы 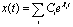, где λ_i- корни характеристического уравнения, умножение x(t) на e^ηt эквивалентно в рассматриваемом случае уменьшению на η действительных корней характеристического уравнения. Т.е. здесь использованное понятие степени устойчивости для линейных систем совпадает с уже известной нам степенью устойчивости η, представляющей собой величину минимальной действительной части корней характеристического уравнения системы (см. (3.60) в подразделе 3.4).
В общем случае нелинейной системы для нахождения величины степени устойчивости η также можно использовать существующие критерии устойчивости нелинейных систем, в частности прямой метод Ляпунова и критерий абсолютной устойчивости В.М. Попова.
Для этого необходимо предварительно в уравнении системы произвести замену переменной x(t) на х(t)^ηt.
Соответственно при применении критерия абсолютной устойчивости В.М. Попова условием наличия у системы степени устойчивости не менее η является выполнение этого критерия для характеристики 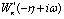вместо 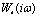(см. подраздел 4.3).
Как и в линейных САУ, при анализе качества нелинейных систем находят величину η, как значение неизвестного параметра, при котором для измененного уравнения система оказывается на границе устойчивости. При синтезе системы могут быть построены линии равных значений η внутри области устойчивости системы в плоскости каких-либо варьируемых параметров. Граница области устойчивости соответствует η = 0.
Рассмотрим возможность определения степени устойчивости η с помощью гармонической линеаризации. Этот метод можно применить для исследования не только гармонических колебаний, но и колебательных переходных процессов. При этом гармоническая линеаризация осуществляется для сигнала на входе нелинейного звена в виде
x(t)=x₀(t)+ae^-ηtsinωt. (4.61)
Коэффициенты гармонически линеаризованного уравнения
нелинейного звена получаются в виде функций неизвестных параметров х₀, а, ω и η искомого решения (4.61). Т.е. в результате исследования определяются перечисленные параметры, включая и величину степени устойчивости η, определяющую время переходного процесса. При синтезе САУ аналогично может быть найдена зависимость η от варьируемых параметров системы, например построением линий постоянных значений η в плоскости этих параметров. Методика здесь та же, что и для определения степени устойчивости линейных САУ, с той только разницей, что применяется она к предварительно линеаризованной системе.
Рассмотрим особенности коррекции динамических свойств нелинейных САУ.
Как и в линейных САУ, коррекция динамических свойств нелинейных систем осуществляется с помощью последовательных и параллельных КЗ. Эти звенья могут быть линейными и нелинейными Линейные КЗ были рассмотрены в подразделе 3.5. Все изложенное выше о них в полной мере справедливо и в случае применения этих звеньев для коррекции нелинейных САУ.
Рассмотрим принципиально новые возможности, возникающие при применении нелинейных звеньев с целью коррекции динамических свойств системы.
Наиболее очевидно эффективное использование нелинейных КЗ для устранения или уменьшения отрицательного влияния на работу системы какой-либо входящей в нее нежелательной нелинейности.
Например, с помощью звена со специально подобранной нелинейной характеристикой может быть изменена статическая характеристика всей САУ в целом. Другой пример - уменьшение влияния насыщения, которое приводит к увеличению длительности переходных процессов, т.е. к снижению быстродействия системы при больших внешних воздействиях. В таких случаях можно добиться значительного ускорения переходных процессов, если линейные КЗ, создающие форсирующее воздействие, заменить или дополнить нелинейными звеньями, которые затягивали бы форсировку, задерживая сигнал на предельно возможном с учетом насыщения значении.
В шестом разделе будет показано, что для получения максимального быстродействия при наличии ограничений на переменные управление должно быть релейным, т.е. нелинейным.
Нелинейная коррекция является более общим средством по сравнению с линейной коррекцией и позволяет повышать качество в том числе и линейных САУ с получением результатов, недостижимых для линейной коррекции.
Например, с помощью нелинейной коррекции в чисто линейной САУ можно устранить известное противоречие между быстро-действием и колебательностью, обеспечив возможность независимого выполнения требований по каждому из этих показателей.
Если в линейной САУ для повышения быстродействия увеличивать коэффициент передачи разомкнутой системы, то предел этому создает возрастающая в конце концов колебательность переходного процесса.
Линейная коррекция позволяет повысить максимально достижимое при этом значение коэффициента передачи, однако принципиально не решает отмеченного противоречия, требующего компромиссного решения при выборе коэффициента передачи и самой коррекции (см. подраздел 3.5).
Это наглядно иллюстрирует рис. 4.27, где приведены переходные характеристики 1, 2 и 3 линейной САУ для трех линейных КЗ, дающих все возрастающую форсировку процесса.

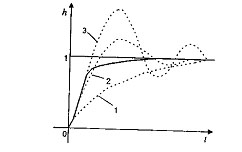
Рис. 4.27 - Переходная характеристика системы при нелинейной коррекции

Противоречие можно устранить, если изменять коррекцию в ходе переходного процесса так, чтобы в первой его части коррекция определялась только по условию обеспечения требования к быстродействию, а затем изменялась на основе требования к устойчивости и колебательности процесса. При этом коррекция, выбранная для первой части переходного процесса, будет настолько сильной, что если ее не изменять к концу, переходный процесс получится с очень большой колебательностью, вплоть до неустойчивости.
Подобное изменение коррекции в ходе переходного процесса означает переход к нелинейной коррекции (см. рис. 4.4), так как сводится к изменению структурной схемы или параметров КЗ в функции переменных величин, характеризующих процессы в системе. При больших отклонениях от установившегося режима, соответствующих началу переходного процесса, коррекция обеспечивает максимально быстрое устранение этого отклонения, а затем, когда отклонение снижено до достаточно малой величины, коррекция обеспечивает неколебательное окончание переходного процесса.
Такая нелинейная коррекция реализуется либо с помощью реле, осуществляющего переключение с одного КЗ на другое в функции выходной величины системы или какой-либо другой переменной, либо с помощью нелинейных звеньев со специально подобранной характеристикой, включенных последовательно с линейными КЗ и изменяющих коэффициент передачи в ходе переходного процесса.
Например, требуемая форсировка при больших отклонениях от установившегося состояния может быть получена включением последовательно в прямой канал САУ или в каналы форсирующих корректирующих воздействий нелинейного звена с характеристикой, приведенной на рис. 4.28, или введением нелинейного звена с выпуклой характеристикой типа характеристики с насыщением в цепь отрицательной обратной связи или в цепь корректирующих воздействий, изменяющих (демпфирующих) переходный процесс.

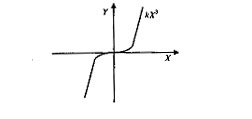
Рис. 4.28 - Статическая характеристика нелинейного К3

Так может быть получен процесс, изображенный на рис. 4.27 сплошной линией. Начальная часть процесса совпадает с переходной характеристикой 3 линейной системы, а далее происходит увеличение демпфирования и процесс переходит в установившееся состояние согласно характеристике 1. Изложенное показывает большие возможности нелинейной коррекции.
Отмечая достоинства нелинейной коррекции, в частности в линейных системах, что она по своей природе является более специализированной по отношению к режимам работы системы, в которых выдает нужный эффект.
Может получится, например, так, что нелинейная коррекция, выбранная для определенного вида внешних воздействий, окажется не только не эффективной, но даже вредной для других неучтенных режимов САУ.
Поэтому, чем шире диапазон внешних воздействий и вообще условий работы системы, тем труднее выбрать нелинейную коррекцию.
К сожалению, общей методики выбора нелинейных КЗ несуществует и практически при синтезе используется метод проб и последовательных приближений, а также опыт и нестрогие рекомендации по применению отдельных частных приемов и схем нелинейной коррекции, описанные в учебной и справочной литературе.