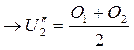Аналитические методы расчета нелинейных цепей

Установившейся режим нелинейной цепи постоянного тока можно опи­сать системой нелинейных алгебраических уравнений Кирхгофа, в которых связь между напряжением и током на нелинейных элементах выражена в виде нелинейного уравнения аппроксимации.

Как известно, в математике не существует общих методов решения сис­тем нелинейных уравнений. В каждом конкретном случае метод решения опре­деляется конкретными условиями задачи: структурой системы уравнений, ти­пом аппроксимации ВАХ нелинейных элементов и другими факторами.

В самых простых случаях возможно выполнить непосредственное реше­ние нелинейного уравнения. Рассмотрим примеры.

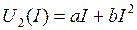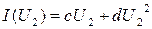Пример 1. Электрическая цепь состоит из последовательно включенных источника ЭДС Е, линейного резистора R₁ и нелинейного резистора НЭ₂ (рис. 213), ВАХ которого аппроксимирована уравнением: а) ; б) ; в) .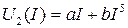

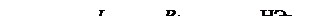
По второму закону Кирхгофа получим уравнение: .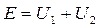

Вид решения этого уравнения зависит от структуры уравнения аппрокси­мации ВАХ.

а) 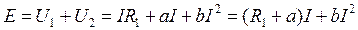- решение задачи сводится к решению квадратного уравнения с неизвестным током I;

б) 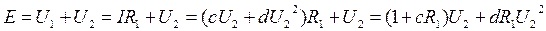- решение задачи сводится к решению квадратного уравнения с неизвестным на­пряжением U₂;

в) 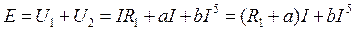- требуется решение алгеб­раического уравнения 5-й степени, что выполнить обычным методом невоз­можно.

В общем случае для решения системы нелинейных алгебраических урав­нений используют так называемый метод последовательных приближений или метод итераций. Сущность данного метода состоит в следующем: задаются в первом приближении значением искомой величины 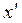. Решают задачу по вы­бранному алгоритму в направлении к источнику, в результате чего определяют расчетное значение ЭДС источника 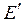. Сравнивают расчетное значение ЭДС источника 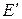с заданным значением Е и с учетом неравенства 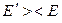задаются значением искомой величины во втором приближении и повторяют расчет по тому же алгоритму. Циклы расчета (итерации) повторяют до достижения же­лаемой точности искомой величины.

Метод последовательных приближений широко используется при расчете нелинейных цепей с помощью ЭВМ. При составлении алгоритма расчета для ЭВМ следует особое внимание обращать на то, чтобы итерационный процесс сходился, в противном случае ЭВМ выдаст ошибку. Рассмотрим несколько примеров.

Пример. Электрическая цепь состоит из последовательно включенных источника ЭДС Е, линейного резистора R₁ и нелинейного элемента НЭ₂ (рис. 213). На рис. 214а, б показаны два варианта ВАХ нелинейного элемента.

По 2-му закону Кирхгофу получим: 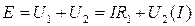или 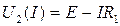. На рис. 114а, б показано графическое решение этого уравнения, где точка n соответствует значению искомой величины (U₂, I).

Составим алгоритм (схему) вычислений для ЭВМ методом последова­тельных приближений. Произвольно задаем первое приближение для напряже­ния на нелинейном элементе 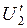. Первое приближение для тока находим по ВАХ нелинейного элемента 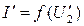. Последующие приближения для напря­жения на нелинейном элементе находим из уравнения 2-го закона Кирхгофа: 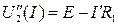, 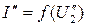; и т. д.

Процесс расчета по этому алгоритму на рис. 214а, б выглядит в виде спи­рали, которая на рис. 214а закручивается вокруг точки n, а на рис. 214б раскручи­ва­ется. Это означает, что в первом случае итерационный процесс сходится и ЭВМ выдаст результаты решения, а во втором случае итерационный процесс расхо­дится и ЭВМ укажет на ошибку программы.

В курсе математики доказывается, что итерационный процесс сходится при условии, если абсолютное значение производной от искомой величины в окрестностях искомого корня (точки n) меньше 1:

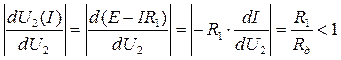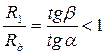или или .

Для решения данной задачи можно составить другую схему вычислений:

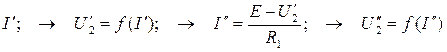; и т. д.

Тогда условие сходимости примет следующий вид:

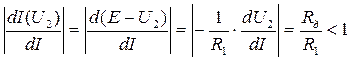или .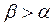

Очевидно, если по первой схеме вычислений итерационный процесс схо­дится, то по второй он расходится, и наоборот.

Схему вычислений на ЭВМ можно организовать по известному из мате­матики методу половинного деления. По этому методу приближение для иско­мой величины устанавливается на середине предполагаемой области его значе­ний. В рассматриваемом примере для напряжения U₂ прилагаемая область зна­чений О₁=0; О₂=Е. Схема вычислений будет иметь вид:

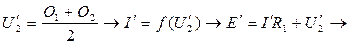
и т. д.

Сходимость итерационного процесса по этой схеме вычислений показана на рис. 215.

В общем случае для сложной цепи быстрота сходимости итерационного процесса зависит от вида ВАХ НЭ, параметров линейных элементов, выбора начальных приближений. Однако основным фактором, определяющим решение нелинейных уравнений итерационным методом, является выбор схемы (алго­ритма) вычислений.

Итерационный метод сегодня является основным методом расчета нели­нейных цепей.