Приближенное исследование стационарных нелинейных систем

Возможность применения метода гармонической линеаризации к стационарным нелинейным системам в основном определяется близостью периодического движения системы к синусоидальному. Это условие обычно удовлетворяется в случае, когда линейные части системы являются фильтрами низких частот. В качестве примера рассмотрим применение метода гармонической линеаризации для системы с одним нелинейным звеном с характеристикой F и линейной частью с передаточной функцией W(p) (рис. 4.23).

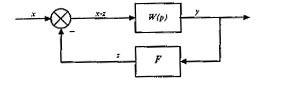
Рис. 4.23 - Одноконтурная нелинейная САУ

Предполагаем, что в нелинейной системе имеются смещенные автоколебания при x ≡ 0, поэтому представим все переменные в виде суммы постоянных составляющих и синусоидальных слагаемых с неизвестными амплитудой, частотой и начальной фазой одного из них:
y = у*+а_ysinω₀t, z = z*+ a_z sin (ω₀t + ψ_z). (4.49)
Проведем гармоническую линеаризацию нелинейного звена, т.е. зависимость z = F(y) заменим приближенной зависимостью:
z = F* + qy + (q'/ω₀) 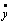или z = F*(a_y,y*) + W_н(a_y,y*)y.
Последнюю формулу перепишем в следующем виде:
z = F*(a_y,y*) + |W_н(a_y,y*)|a_ysin(ω₀t + ψ_н), (4.50)
где W_н(аy,y) - комплексный гармонический коэффициент усиления, ψ_н = argW_н(a_y, y*).
Выходную переменную у линейной части системы на основе принципа суперпозиции (1.1) можно представить через переменную z в следующем виде:
у = -W(0)z* -|W(iω₀)|a_zsin[ω₀t + ψ_z+ ψ( ω₀)]. (4.51)
Из равенства правых частей формул (4.49) и (4.50) для z и в формулах (4.49) и (4.51) для у получим:
z* +a_zsin(ω₀t + ψ_z) = F*(a_y, y*)+|W_н(a_y, y*)|a_ysin(ω₀t + ψ), (4.52)
у*+аysinω₀t = -W(0)z* -|W(iω₀)|аz sin[ω₀t + ψ_z + ψ(ω₀)]. (4.53)
Сравнивая в правых и левых частях уравнений (4.52) и (4.53) постоянные составляющие, амплитуды и фазы синусоидальных составляющих, получим уравнения:

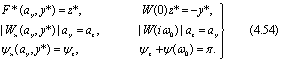
Исключая из уравнений (4.54) переменные a_z, z*, ψ_z, получим три уравнения для определения искомых переменных y*, a_y, ψ₀:
y*= -W(0)F*(a_y,y*), (4.55)
|W(iψ₀)|•|W_н(a_y, y*)| = 1, (4.56)
argW(iψ₀) + argW_н(a_y, y*) =iπ. (4.57)
Получить аналитическое решение уравнений (4.55)-(4.57) в общем виде невозможно. Для их решения применяются различные приближенные методы.
Удобно также воспользоваться графическими способами.
Рассмотрим возможные способы графического решения этой системы уравнений.
Первый способ состоит в следующем. На координатной плоскости 0у*а_y (рис.4.24) по уравнению (4.55) построим кривую 1. Затем при определенных значениях ω₀ задаемся значениями у* и определяем из уравнений (4.56) и (4.57) соответствующие значения а_y.

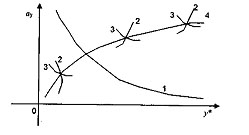
Рис. 4.24 - Графическое решение уравнений (4.54)

По результатам этих вычислений для различных конкретных значений ω₀ строим кривые 2, соответствующие уравнению (4.56), и кривые 3, соответствующие уравнению (4.57). Точка пересечения кривых 2 и 3 на рис. 4.24 является совместным решением уравнений (4.56) и (4.57) для конкретного значения ω₀.
Построив кривые 2 и 3 для ряда значений ω₀, соединим точки их пересечения кривой 4. Точка пересечения кривой 4 и кривой 1 определяет искомые значения у* и a_y, удовлетворяющие всем трем уравнениям (4.55), (4.56) и (4.57). Для определения частоты автоколебаний ω₀ следует подставить найденные значения у* и a_y в уравнение (4.56) или в уравнение (4.57).
Частоту автоколебаний можно также определить по шкале значений ω₀, полученной на кривой 4 (рис. 4.24) при ее построении по достаточно большому числу точек. Однако этот способ менее точен, чем предыдущий.
Второй способ отличается от первого способа только приемом отыскания кривой 4 для рис. 4.24.
Объединим уравнения (4.56) и (4.57) в одно уравнение
W(iω₀)W_н(a_y,y*) = -1 (4.58)
и перепишем его в виде :
W(iω₀) = -1/W_н(a_y,y*). (4.59)
Построим на комплексной плоскости (рис. 4.25) АФХ линейной части системы W(iω) и обратную АФХ нелинейного звена со знаком "-", т.е. -1/W_н(a_y,y*) для разных значений y* при изменении ω₀ и а_y от 0 до ∞.

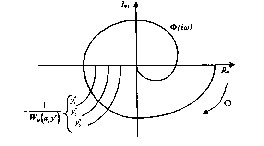
Рис. 4.25 - Графическое решение уравнения (4.59)

Точки пересечения этих характеристик определяют зависимость ау=f(y*), соответствующую уравнению (4.59), т.е. кривую 4 для рис.4.24. Далее определяем на рис. 4.24 точку ее пересечения с кривой 1, построенной по уравнению (4.55). Определяем ω₀ аналогично первому способу.
Для совместного решения уравнений (4.55) - (4.57) используются также ЛЧХ.
Если не существует действительных значений у* и положительных значений а_y и ω₀, удовлетворяющих уравнениям (4.55)-(4.57), то автоколебания в системе невозможны.
После определения путем решения уравнений (4.55)-(4.57) параметров периодического движения системы необходимо оценить устойчивость этого движения, что подтвердит его соответствие реально существующим в системе автоколебаниям. Особенно важно это проверить при наличии нескольких периодических решений.
Для исследования устойчивости периодического движения системы можно применить первый метод Ляпунова, т.е. составить соответствующие уравнения в вариациях и исследовать устойчивость определенной ими линеаризованной системы.
Приближенно оценить устойчивость автоколебаний можно на основе следующих рассуждений.
Движение системы, близкое к найденному периодическому, можно приближенно считать синусоидальным с медленно изменяющейся амплитудой А, приближающейся к амплитуде автоколебаний а_у. в случае устойчивых автоколебаний и удаляющейся от а_у в случае неустойчивых автоколебаний.
Если автоколебания в системе устойчивы и имеют амплитуду a_y, то при замене ее в уравнении (4.58) величиной А > a_y пара чисто мнимых корней ±iω₀ должна замениться парой комплексных сопряженных корней с отрицательной действительной частью, а при замене а_у величиной А < a_y корни ±iω₀ должны замениться парой комплексных сопряженных корней с положительной действительной частью.
Для проверки характера изменения корней ±iω₀ при замене в уравнении (4.58) величины a_y величиной А удобно использовать критерий Найквиста.
Так как уравнение (4.58) имеет чисто мнимые корни ±iω₀ при А=ау, то АФХ разомкнутой системы
Wp (iω₀,a_y,y) = W(iω)W_н(u,y*) (4.60)
при А = a_y проходит через точку минус 1 плоскости комплексной переменной (рис. 4.26 - кривая 1).

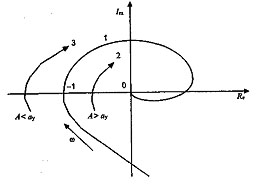
Рис. 4.26 - Проверка устойчивости автоколебаний

В случае неустойчивых автоколебаний должна наблюдаться обратная картина.
В случае полуустойчивого предельного цикла кривая (4.60) смещается в одну и ту же сторону при А > a_yи при А < a_y.