Гармоническая линеаризация

В связи с трудностью точного исследования нелинейных систем выше третьего порядка большое значение имеют приближенные методы, хорошо зарекомендовавшие себя на практике Для систем, близких к линейным, часто применяется так называемый метод малого параметра, основанный на разложении неизвестных элементов движения системы в степенные ряды относительно малого параметра. Если совокупность нелинейных членов в дифференциальных уравнениях системы мала по сравнению с каждым из линейных членов, то этот метод дает хорошие результаты. Малым параметром в этом случае является искусственно вводимый или естественно присутствующий в уравнениях системы общий постоянный множитель всех нелинейных членов. Однако наиболее мощным и вследствие этого наиболее распространенным приближенным методом исследования нелинейных систем является метод гармонической линеаризации. Поэтому ограничимся изложением только этого метода.
Методом гармонической линеаризации можно относительно просто и с достаточной точностью исследовать многие типы стационарных нелинейных систем. Он позволяет оценивать устойчивость нелинейных систем, определять амплитуду и частоту автоколебаний, а также выбирать корректирующие звенья, обеспечивающие желаемые характеристики нелинейных систем.
Применение метода гармонической линеаризации предполагает существование в системе сигнала, близкого к синусоидальному, на основании чего осуществляется гармоническая линеаризация характеристик нелинейных звеньев.
Рассмотрим действие на нелинейное звено сигнала в виде синусоидальных колебаний, с постоянной амплитудой а:
х=asinωt . (4.37)
Выходной сигнал нелинейного звена, характеристика которого имеет вид (4.1), в этом случае также будет периодическим, но при гармонических колебаниях входной переменной х колебания выходной переменной у нелинейного звена уже не будут гармоническими.
Известно, что любая периодическая функция может быть разложена в ряд Фурье, поэтому выходной сигнал нелинейного звена при синусоидальном входном сигнале может быть представлен формулой:

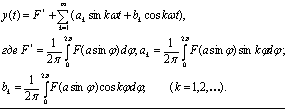
Величина F* представляет собой постоянную составляющую или среднее значение выходного сигнала у. Амплитуды a_k и b_k гармонических составляющих выходного сигнала у быстро уменьшаются с увеличением номера составляющей. Таким образом, в отличие от линейных звеньев, нелинейные звенья реагируют на гармонические колебания одной определенной частоты гармоническими колебаниями разных частот (теоретически - это бесконечная последовательность частот). В сумме эти гармонические колебания дают негармонические колебания выходного сигнала.
В САУ нелинейное звено практически всегда включается последовательно с линейными частями системы. Линейная часть, как правило, является фильтром низких частот и подавляет высокочастотные колебания. Поэтому имеются основания пренебречь гармониками выше первой на выходе нелинейного звена. Тогда, с учетом (4.37), получим приближенную линейную зависимость выходной переменной нелинейного звена от его входной переменной:

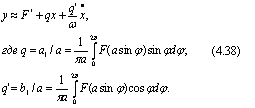
Таким образом, под действием гармонических колебаний нелинейное звено как бы линеаризуется и может рассматриваться приближенно как линейное звено. Коэффициенты q и q' называются гармоническими коэффициентами усиления нелинейного звена. Из формул для коэффициентов видно, что F*, q и q' зависят от амплитуды входного сигнала а. Эта зависимость отражает нелинейные свойства звена и из-за нее принцип суперпозиции (1.1) неприменим для гармонически линеаризованного нелинейного звена. Приближенное представление нелинейной зависимости y = F(x) при синусоидальном входном сигнале линейной зависимостью (4.38) называется гармонической линеаризацией. А основанный на этом приеме метод исследования нелинейных систем называется методом гармонической линеаризации или методом гармонического баланса (основы метода заложены Н.М. Крыловым и Н.Н. Боголюбовым, а в применении к автоматическим системам он иногда называется методом Л.С. Гольдфарба).
Отметим, что для любой нечетной характеристики F функция F* равна нулю, а для любой однозначной характеристики F второй коэффициент q' равен нулю (это соответствует отсутствию сдвига фаз между первой гармоникой на выходе нелинейного звена и входным синусоидальным сигналом):
Выражение (4.38) можно также представить в виде

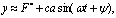(4.39)
где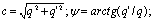
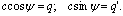(4.40)
Величина с характеризует усиление амплитуды, а ψ-сдвиг фазы гармонических колебаний нелинейного звена. Отметим, что в отличие от линейных систем усиление амплитуды и сдвиг фазы гармонически линеаризованным нелинейным звеном зависят от амплитуды входного сигнала. Запишем гармонический входной сигнал в комплексной форме: х=aе^iωt. Тогда первая гармоника выходного сигнала примет вид:
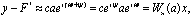(4.41)
где W_н(a)=се^iψ - комплексный гармонический коэффициент усиления (или амплитудно-фазовая характеристика, гармонический коэффициент передачи, описывающая функция) нелинейного звена.
Используя (4.40) и (4.41), получим для комплексного гармонического коэффициента усиления другое выражение:
W_н(a) = q(a) + iq'(a).
Комплексный гармонический коэффициент усиления безынерционного нелинейного звена (или его АФХ) не зависит от частоты, но зависит от амплитуды гармонических колебаний. В этом состоит основное отличие нелинейного безынерционного звена от линейного инерционного.
Для линейного звена АФХ не зависит от амплитуды, но зависит от частоты входных гармонических колебаний.