Проблема Айзермана. Критерий абсолютной устойчивости В.М. Попова

Абсолютная устойчивость - это устойчивость в целом нелинейной системы при задании ее нелинейностей принадлежностью к определенному классу. Под этим понимается задание нелинейности не конкретной характеристикой, а в более общем виде с точностью до определения класса нелинейностей.
Наиболее разработаны методы исследования абсолютной устойчивости для нелинейных систем (рис. 4.13), состоящих из линейного звена и нелинейной обратной связи, статическая характеристика которого представлена на рис. 4.14, т.е. статическая нелинейная характеристика находится в определенном угле между прямыми линиями λ₁x и λ₂x.

Рис. 4.13 - Нелинейная система (пример)

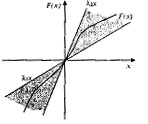
Рис. 4.14 - К понятию абсолютной устойчивости

Это условие обычно записывается в виде
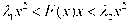(4.30)
для всех х ≠ 0.
Если в системе такого типа положить F = λx, то в плоскости х, F(x) может быть проведен луч через начало координат, такой, что при любом х из этого луча соответствующая линейная система устойчива.
В 1949 г. М.А. Айзерман выдвинул гипотезу о том, что если асимптотически устойчивы все линейные системы, для которых
(φ) = λ(λ = const) и выполнено условие (4.30), то этим же свойством обладает все семейство нелинейных систем, характеризующееся условием (4.30). Такие системы были названы абсолютно устойчивыми. Исследования показали, что для систем второго порядка гипотеза верна, исключая случай асимптотического приближения траектории к краям луча, но для систем более высокого порядка были разработаны примеры, противоречащие этой гипотезе. В 1951 г. А.И. Лурье предложил использовать функцию Ляпунова, квадратичная форма которой дополнена интегралом от нелинейной характеристики F(x) или F(x,t). Однако это дополнение лишь расширило луч, обеспечивающий абсолютную устойчивость. В 1960 г. на первом конгрессе ИФАК румынский ученый В.М. Попов доложил неожиданный результат : можно построить аналог частотной характеристики линейной части системы, которого достаточно для определения луча. Рассмотрим подробнее критерий абсолютной устойчивости В.М. Попова.
Характеристика F(x) (рис.4.13) однозначна и лежит в углу
(0,k), т.е. (λ₁ = 0, λ₂ = k). Для определения устойчивости по этому критерию используется частотная характеристика

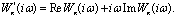
Эта характеристика получается из АФХ W_л(iω) линейной части системы путем умножения ординат последней характеристики на текущее значение ω.
Рассмотрим вначале критерий В.М. Попова для случая, когда линейная часть системы устойчива. Система абсолютно устойчива, если при устойчивой линейной части системы через точку (-1/k,i0) можно провести хотя бы одну прямую линию так, чтобы характеристика W*_л(iω) находилась от нее справа (рис. 4,15). Такая линия называется линией Попова

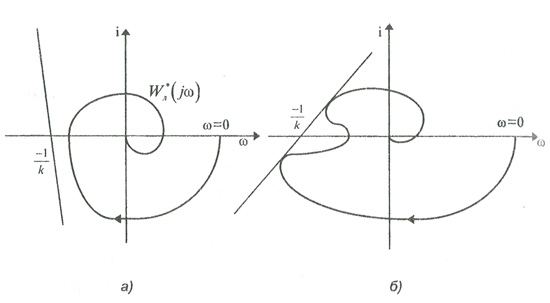
Рис. 4.15 - Критерий В.М.Попова для системы с устойчивой линейной

частью: а - критерий выполняется, б - критерий не выполняется

Критерий В.М. Попова является достаточным, т.е. он дает часть области абсолютной устойчивости и его невыполнение не означает отсутствия абсолютной устойчивости.
Чтобы распространить этот критерий на системы с неустойчивой линейной частью, преобразуем предварительную схему системы (см. рис. 4.13): введем два фиктивных звена с коэффициентом передачи к_ф (рис. 4.16). Они ничего не изменят в системе, так как их выходные сигналы взаимно компенсируют друг друга на входе линейной части системы.
В результате получим систему, состоящую из линейной части передаточной функиции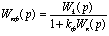

и нелинейной части с характеристикой F_ф(x) = F(x) - k_фx
Выберем величину k_ф такой, чтобы новая линейная часть оказалась устойчивой. Применим к преобразованной системе с устойчивой линейной частью критерий В.М. Попова.

В результате получим следующее условие абсолютной устойчивости исходной системы с неустойчивой линейной частью : система абсолютно устойчива, если через точку (-1/(к-k_ф),0) можно провести прямую линию, проходящую слева от характеристики W*_лф(iω), т.е. характеристика F(x) (рис.4.16, б) должна лежать в углу (k_ф,к).

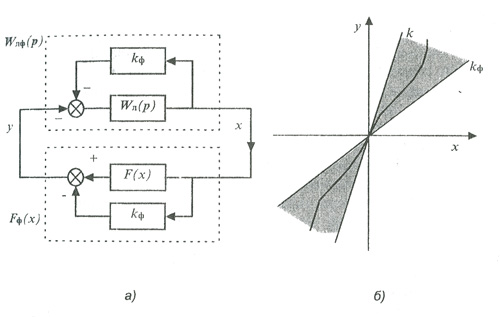
Рис. 4.16 - К абсолютной устойчивости системы с неустойчивой линейной частью

Этот вывод следует из того, что характеристика F_ф(х) (4.31) расположена в угле [0, (к-к_ф)\.
В 1966 г. В.М. Попов доказал, что аналогично может быть определен луч, который обеспечивается как функцией Ляпунова в виде квадратичной формы, так и функцией Ляпунова в форме Лурье.
Исследования по проблеме абсолютной устойчивости продолжаются, но найти наиболее широкий луч абсолютной устойчивости до сих пор не удалось.