Анализ типовых схем базирования.

Заготовка прижата силой Qз, концевой фрезой фрезеруется уступ, выдерживая размеры А, В, Е. Станок предварительно настроен.

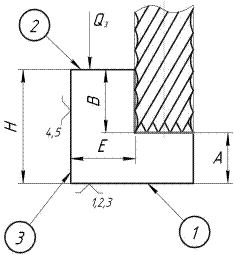
	Необходимо проанализировать погрешность базирования при получении размеров А, В, Е. Н – высота детали, А – настроечный размер.
Рисунок 2.15 Пример схемы базирования плоскими поверхностями.

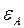=0 и =0- т. к. технологическая и измерительная базы совпадают,

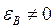- так как измерительной базой является поверхность 2, а технологической базой - поверхность 1.

Составляем размерную цепь

В=Н-А

А- настроечный размер, значит А=const.

Таким образом, действительная погрешность базирования для размера В, будет зависеть от допуска на размер Н:

.

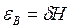Чтобы получить 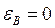, необходимо совместить ТБ с ИБ (перевернуть заготовку), т.е. переустановить ее на поверхность 2.

2.Установка наружными цилиндрическими поверхностями.

Размеры валов в обрабатываемой партии всегда имеют некоторый разброс по диаметру. Так при фрезеровании лысок и шпоночных пазов на валах размеры последних могут быть заданы как 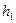, 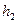или .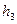

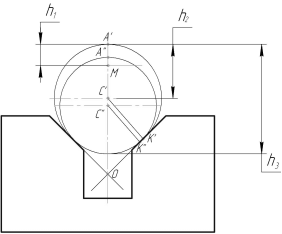
Рисунок 2.16 Пример базирования наружными цилиндрическими поверхностями.

Но так как диаметральные размеры обрабатываемых валов изменяются от некоторого минимального до максимального значений, положение из осей может быть расположено в точках 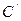или 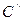. Соответственно положение верхней точки А также может изменяться.

Требуется проанализировать возникающие погрешности базирования когда размер задан одним их трех способов: как 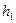, 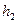или .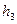

а) выдерживаемый размер задан как h3.

Составим размерную цепь

h=ОА-ОМ

АО - настроечный размер (отрезок), АО=const и на погрешность базирования не влияет.

После тригонометрических преобразований получим, что погрешность базирования будет определяться формулой

=

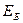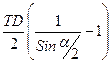
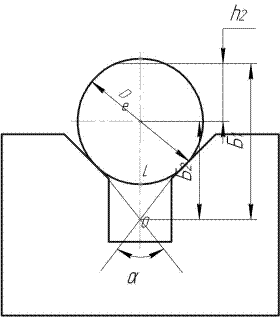
б) выдерживаемый размер задан как h2

	Строим размерную цепь H2=Б1-Б2 Б1 – является настроечным размером, значит вся погрешность связана с размером Б2. =
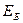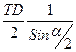
Рисунок 2.17 Пример базирования вала на призме.

в) размер задан как h1 (от верхней точки) и, проведя аналогичные рассуждения получим:

= .

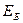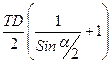Таким образом, рассмотрев три возможных варианта простановки размеров: 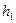, 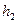или как 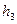делаем вывод, что минимальная погрешность базирования будет иметь место, если выдерживаемый размер задан как .

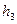В практике встречаются и другие подходы к снижению погрешности базирования:

А) за счет изменения положения призмы,

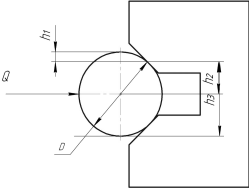
Рисунок 2.18 Пример изменения базирования вала с использованием призмы.

Б) за счет уменьшения допусков на диаметр D,

В) за счет изменения (замены) схемы базирования.

Возможны и другие решения.