Исследование нелинейных систем методом точечных преобразований

Метод точечных преобразований (отображений), берущий свое начало от Пуанкаре и Биркгофа, был впервые введен в ТАУ А.А. Андроновым. Основные общие рекомендации по применению теории точечных отображений к изучению конкретных нелинейных САР и радиотехники сформулированы А.А. Андроновым в 1944 г. в докладе на сессии отделения физико-математических наук АН СССР "Теория точечных преобразований Пуанкаре-Брауера-Биркгофа и теория нелинейных колебаний". В это же время им был решен ряд основных нелинейных задач ТАР, в том числе и классическая задача И.А. Вышнеградского о регуляторе прямого действия с сухим трением в чувствительном элементе. В основе этих и многочисленных последующих работ (продолжающихся и в настоящее время) лежит кусочно-линейная аппроксимация нелинейностей, которая обеспечивает получение аналитических выражений точечного преобразования в явном или параметрическом виде. Именно этим обстоятельством объясняется то, что в учебной и справочной литературе по ТАУ метод точечных отображений определен как метод исследования кусочно-линейных систем невысокого порядка. Ю.И. Неймарк в монографии "Метод точечных отображений в теории нелинейных колебаний" (1972 г.) отмечает, что сам А.А. Андронов рассматривал кусочно-линейные системы как частный тип нелинейных систем, для которых исследование методом точечных преобразований может обеспечить быстрый успех, а исследование кусочно-линейных систем, как старт развитию метода точечных преобразований применительно к задачам теории колебаний. Ю.И. Неймарк и его нижегородская научная школа рассматривают точечные отображения в качестве общего средства описания и эффективного аппарата исследования теории колебаний как науки об общих закономерностях динамических процессов.
Для пояснения идеи метода точечных преобразований предположим, что изображающая точка в какой-то момент времени занимает положение X (рис. 4.17) с координатой х на положительной полуоси 0x₁. После обхода вокруг начала координат изображающая точка пересечет полуось 0x₁ в некоторой точке Y, имеющей координату у. Через каждую точку полуоси 0x₁ можно провести одну и только одну фазовую траекторию, поэтому обходу изображающей точки вокруг начала координат соответствует переход каждой точки полуоси 0x₁ в некоторую другую точку той же полуоси.

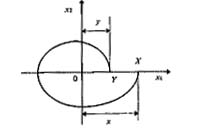
Рис. 4.17 - Точечное преобразование полуоси Ох₁ в саму себя

Другими словами, обходу изображающей точки вокруг начала координат (либо другой особой точки на фазовой плоскости) соответствует точечное преобразование любой полуоси (в общем случае - полупрямой), выходящей из начала координат, в саму себя. Если при этом преобразовании какая-нибудь точка полуоси (полупрямой) переходит в саму себя, т.е. остается неподвижной, то через эту точку проходит замкнутая фазовая траектория - предельный цикл. Таким образом, для нахождения предельных циклов и определения параметров соответствующих автоколебаний достаточно найти неподвижные точки точечного преобразования какой-либо полупрямой, выходящей из соответствующей особой точки фазовой плоскости.
Каждой точке выбранной полупрямой соответствует некоторое положительное число, равное расстоянию этой точки от начала координат (или от соответствующей особой точки).
Поэтому точечное преобразование выбранной полупрямой при обходе изображающей точки вокруг начала координат (особой точки) определяет однозначную возрастающую функцию y=f(x), которая может быть изображена кривой в координатах 0xy (рис. 4.18).
Определение у по х (т.е. нахождение точки Y по точке X) называется точечным преобразованием. Зависимость y=f(x) описывает точечное преобразование положительной полуоси 0x₁ в саму себя, происходящее при обходе изображающей точки начала координат.
Каждая точка этой кривой с одинаковыми абсциссой и ординатой, т.е. точка пересечения ее с биссектрисой (рис. 4.18 -штрих-пунктирная линия) координатного угла у=х является неподвижной точкой преобразования, определяет предельный цикл и амплитуду возможных автоколебаний в системе.

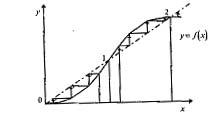
Рис 4.18 - Функция точечного преобразования

Участкам кривой у = f(х), лежащим ниже биссектрисы координатного угла у=х, соответствуют спиральные фазовые траектории, по которым изображающая точка приближается к началу координат, т.е. колебательный процесс является затухающим. Участкам кривой у = f(x), лежащим выше биссектрисы координатного угла у=х, соответствуют спиральные фазовые траектории, по которым изображающая точка удаляется от начала координат, следовательно, колебательный процесс является расходящимся. Таким образом, вид функции у = f(x) и взаимное расположение кривой точечного преобразования у=f(x) и биссектрисы координатного угла у=х позволяют судить' о характере поведения нелинейной системы около положения равновесия. При этом, если кривая y=f(x) пересекает биссектрису у=х сверху вниз (рис. 4.18 - точка 2), то автоколебания устойчивы, а если снизу вверх (рис. 4.18 - точка 1) - неустойчивы.
Метод точечных преобразований позволяет исследовать характер возможных режимов в системе, не строя фазового портрета. Метод удобен, в частности, для определения влияния изменения разных параметров системы на характер переходных процессов в ней. При этом могут быть определены критические, так называемые бифуркационные значения параметров, переход через которые качественно меняет фазовый портрет системы.
Для иллюстрации на рис. 4.19 показано возможное изменение диаграммы точечного преобразования системы при вариации ее параметров. График 3 соответствует устойчивости в целом. Кривая 2 касается биссектрисы в точке, соответствующей полуустойчивому циклу. Эта кривая определяет бифуркационные значения параметров системы, при которых система находится на границе между качественно различными типами фазового портрета.

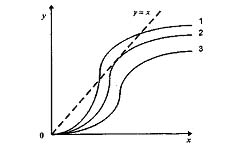
Рис. 4.19 - Влияние параметров системы на диаграмму точечного преобразования

При бесконечно малом отклонении параметров в одну сторону система становится устойчивой в целом (рис.4.19 - кривая 3), а при отклонении параметров в другую сторону система становится устойчивой только в малом с переходом к устойчивым автоколебаниям при больших отклонениях от установившегося режима (рис. 4.19 - кривая 1). Заметим, что если кривая y=f(x) и прямая у=х не пересекаются (рис. 4.19 - кривая 3), то предельного цикла не существует и автоколебания в системе невозможны.
Для многих систем фазовая плоскость оказывается симметричной относительно оси абсцисс и оси ординат. При исследовании таких систем удобно рассматривать преобразование полуоси x₁ > 0 в полуось x₁ < 0 при полуобходе изображающей точки вокруг начала координат.
Этому полуобходу также соответствует некоторая функция y=f(х).
Если на фазовой плоскости имеются линии переключения, то удобнее изучать точечные преобразования какой-нибудь линии переключения в саму себя.
Метод исследования нелинейных систем с помощью фазовой плоскости и метод точечных преобразований наглядны и сравнительно просты для систем второго порядка. Для систем третьего порядка эти методы значительно усложняются. Для систем выше третьего порядка точные методы исследования нелинейных систем в своей традиционной форме практически неприменимы.
Существует 55-летняя традиция успешного применения метода точечных преобразований для исследования кусочно-линейных систем невысокого порядка. Решим задачу составления уравнений точечных преобразований на примере исследования следящей системы. Уравнение для отклонений данной системы при наличии сил сухого трения имеет следующий вид:
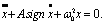(4.32)
Легко увидеть, что уравнение (4.32) является частным случаем рассмотренной выше динамической нелинейности (4.6).
В данном примере исследуется свободное движение следящей системы (правая часть уравнения равна нулю) и предполагается
отсутствие застоев (4.7), т.е. характеристика сухого трения сводится к идеальной релейной характеристике (см. рис. 4.3, а, рис. 1.8, б-1), поэтому отсутствует второй член из уравнения (4.6). Следовательно, (4.6) для нашего примера запишется в виде
mp²y + csignpy + k₂y = 0. (4.33)
Разделив каждое слагаемое на массу m и произведя замену у=х; А=с/m; 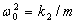, получим из (4.33) уравнение (4.32). При 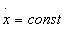уравнение (4.32) линейно и его решение
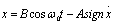, (4.34)
где В определяется из начальных условий.
В нашем примере уравнение линии переключения 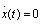. Построим точечное преобразование этой линии переключения в саму себя. Пусть 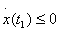, тогда согласно (4.34) имеем x(t_1i) = B_icosω₀t₁ + A, а при 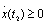из (4.34) получим x(t_2j) = -C_jcosω₀t₂ - A, где B_i и С_j - постоянные, зависящие от начальных условий и числа переключений на линии 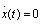. Определим разностное уравнение, связывающее между собой
значения В и С.
Пусть условие 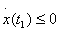выполняется с момента времени t_1,2k, тогда спустя полпериода имеем
-B_2k+A = -C_2k+1 - A. (4.35)
Спустя еще полпериода будем иметь
C_2k+1 - A = B_2k+1 + A. (4.36)
Уравнения (4.35) и (4.36) являются уравнениями точечных преобразований и позволяют вычислить значение C_2k+1, если известно B_2k, а если известно C_2k+1, то вычислить значение B_2(k+1). Из уравнений (4.35) и (4.36) получим, например, следующее соотношение: В_i+1 = В_i - 4А, где i = 2k . Задавая В₀ = х-А, получим B₁ = x - 5A, В₂ = x - 9А и т.д.
Решение заканчивается, когда В_i, становится меньше А.
Продолжим изучение этого примера и построим фазовый портрет следящей системы при учете сил сухого трения. При А=0 система консервативна и решение (4.34) запишется в виде x=Bcosω₀t. Обозначая х = х₁, 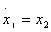, получим:
;

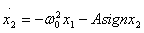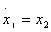
или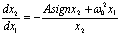
Интегрируя это выражение и считая знак х₂ неизменным, получим

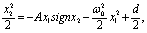
где d определяется начальными условиями. Введя относительную координату 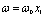, получим

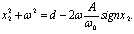
Это уравнение окружности, координаты центра которой смещены относительно начала координат по оси ω на величину минус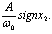
На рис. 4.20 представлено семейство фазовых траекторий, соответствующее рассматриваемому случаю.

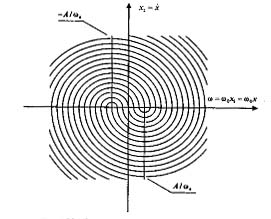
Рис. 4.20 - Фазовый портрет следящей системы при учете сил сухого трения

Уравнением линии переключения является х₂ = 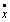= 0.
Выше этой линии фазовые траектории представляют собой полуокружности радиуса 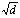, (d- любое число), проведенные относительно точки минус 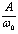; ниже этой линии - полуокружности с центром в точке .
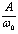Из рис. 4.20 видно, что сухое трение стабилизирует систему, превращая ее в устойчивую. Когда |ω| становится меньше 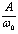, процессы заканчиваются, появляется зона нечувствительности.