ЭЛЕМЕНТЫ МЕХАНИКИ ЖИДКОСТЕЙ И ГАЗОВ
План
1. Основные задачи механики жидкости и газов.
2. Понятия сжимаемости и вязкости. Поле скоростей, линии и трубки тока, стационарное течение.
3. Уравнение неразрывности и уравнение Бернулли.
4. Течение вязкой жидкости. Формула Пуазейля.
5. Ламинарный и турбулентный режимы течения.
6. Циркуляция скорости. Потенциальное и вихревое движение. Формула Жуковского.
1. Основные задачи механики жидкостей и газов:
1. Определение усилий, действующих на тела, движущиеся в жидкости или газе, например определение силы лобового сопротивления самолёта для расчета мощности его двигателя, определение силы торможения парашюта, расчёт ветровой нагрузки телебашен, линий электропередач и т.д.
2. Определение наиболее выгодных форм тел, например формы крыльев самолёта, корпуса подводной лодки, лопаток турбины и т.п.
3. Определение режима течения в каналах, трубах. Если, например, ламинарный режим изменяется на турбулентный, то изменяются и уравнения, описывающие течения, и конечные решения.
4. Изучение распространения механических волн, например распространения ультразвуковых волн при локации кораблей и подводных лодок, изучение закономерностей ударных волн, возникающих при взрыве атомных бомб, от самолётов, движущихся со скоростями больше скорости звука в атмосфере.
2. Понятие о сжимаемости и вязкости. Пусть имеется деформируемое тело длиной L, которое мы в некоторый момент начнём толкать слева направо со скоростью 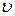 (рис. 5.1). Придёт ли всё тело сразу в движение со скоростью
(рис. 5.1). Придёт ли всё тело сразу в движение со скоростью 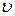 ? Нет. Левый конец начнёт двигаться сразу. По телу от левого конца к правому побежит волна упругого воздействия со скоростью звука
? Нет. Левый конец начнёт двигаться сразу. По телу от левого конца к правому побежит волна упругого воздействия со скоростью звука 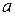 . В течение времени
. В течение времени 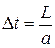 правый конец не будет «знать», что левый конец двигается, и будет стоять. За это время левый конец пройдёт расстояние
правый конец не будет «знать», что левый конец двигается, и будет стоять. За это время левый конец пройдёт расстояние 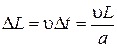 . Тело станет короче на величину
. Тело станет короче на величину 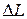 , т.е. сожмётся на эту величину. Относительное сжатие тела будет:
, т.е. сожмётся на эту величину. Относительное сжатие тела будет:
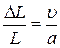 .
.
 Отношение
Отношение 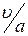 обозначают числом
обозначают числом 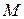 и называют числом Маха по имени австрийского физика и философа Эрнста Маха (1838 – 1916). Видно, что сжимаемость равна отношению скорости движения к местной скорости звука – числу Маха. Чем больше скорость звука в веществе, тем меньше его сжимаемость. Скорость звука в воздухе примерно равна 330, в воде – 1400 и в металлах – 4000 – 7000 м/c.
и называют числом Маха по имени австрийского физика и философа Эрнста Маха (1838 – 1916). Видно, что сжимаемость равна отношению скорости движения к местной скорости звука – числу Маха. Чем больше скорость звука в веществе, тем меньше его сжимаемость. Скорость звука в воздухе примерно равна 330, в воде – 1400 и в металлах – 4000 – 7000 м/c.
Условно считают, что если 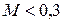 , то жидкость несжимаемая, а если
, то жидкость несжимаемая, а если 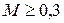 , то жидкость сжимаемая. Например, если пуля летит со скоростью примерно 800 м/с в воде, то
, то жидкость сжимаемая. Например, если пуля летит со скоростью примерно 800 м/с в воде, то 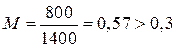 . Поэтому вода для летящей пули – сжимаемая жидкость.
. Поэтому вода для летящей пули – сжимаемая жидкость.
Вязкость. Все реальные жидкости являются вязкими. Вязкость (внутреннее трение) проявляется в том, что при движении в жидкости тело встречает сопротивление. Из опыта известно: чтобы поддерживать постоянным течение жидкости в трубе, необходимо наличие между концами трубы разности давлений. Необходимость сил давления указывает на то, что эти силы уравновешиваются какими-то силами, тормозящими движение. Этими силами являются силы внутреннего трения на границе со стенкой трубы и на границах между слоями. Более быстрый слой стремится увлечь за собой более медленный слой, действуя на него с силой 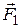 , направленной по течению. Одновременно более медленный слой стремится замедлить движение более быстрого слоя, действуя на него силой
, направленной по течению. Одновременно более медленный слой стремится замедлить движение более быстрого слоя, действуя на него силой 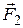 , направленной против течения (рис. 5.2). Экспериментально установлено, что модуль силы внутреннего трения, приложенной к площадке S, лежащей на границе между слоями, определяется формулой:
, направленной против течения (рис. 5.2). Экспериментально установлено, что модуль силы внутреннего трения, приложенной к площадке S, лежащей на границе между слоями, определяется формулой:


где 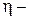 коэффициент пропорциональности, зависящий от природы жидкости и её состояния (например температуры);
коэффициент пропорциональности, зависящий от природы жидкости и её состояния (например температуры); 
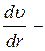 производная скорости жидкости по радиусу, показывающая, как быстро изменяется в данном месте скорость течения в направлении оси r, перпендикулярной к площадке S.
производная скорости жидкости по радиусу, показывающая, как быстро изменяется в данном месте скорость течения в направлении оси r, перпендикулярной к площадке S.
Под идеальной жидкостью понимают жидкость, в которой нет сил внутреннего трения, т.е. вязкость равна нулю (более строго говорят, что жидкость не оказывает сопротивления деформации сдвига).
 Поле скоростей. Движение жидкости характеризуется совокупностью функций
Поле скоростей. Движение жидкости характеризуется совокупностью функций 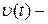 скоростей, с которыми проходят через каждую точку отдельные частицы жидкости. Совокупность векторов
скоростей, с которыми проходят через каждую точку отдельные частицы жидкости. Совокупность векторов 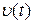 , заданных для всех точек пространства течения жидкости, называется полем вектора скорости. Это поле наглядно можно изобразить с помощью линий тока. Линия тока – такая линия, в каждой точке которой в данный момент времени вектор скорости направлен по касательной.
, заданных для всех точек пространства течения жидкости, называется полем вектора скорости. Это поле наглядно можно изобразить с помощью линий тока. Линия тока – такая линия, в каждой точке которой в данный момент времени вектор скорости направлен по касательной.
Поверхность тока – совокупность линий тока, проходящих через некоторую кривую (рис. 5.3). Часть жидкости, ограниченная замкнутой поверхностью тока, называется трубкой тока. Если скорость в каждой точке пространства остаётся постоянной ( 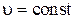 ), то течение жидкости называется стационарным (установившимся).
), то течение жидкости называется стационарным (установившимся).
 3. Уравнение неразрывности. Пусть имеется достаточно тонкая трубка тока (скорость во всех точках поперечного сечения одинакова) несжимаемой жидкости. При стационарном течении трубка тока подобна стенкам жёсткой трубы. Поэтому через сечение S за время
3. Уравнение неразрывности. Пусть имеется достаточно тонкая трубка тока (скорость во всех точках поперечного сечения одинакова) несжимаемой жидкости. При стационарном течении трубка тока подобна стенкам жёсткой трубы. Поэтому через сечение S за время 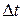 пройдёт объём жидкости
пройдёт объём жидкости 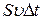 , а в единицу времени
, а в единицу времени 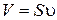 .
.
Возьмём 2 сечения трубки тока (рис. 5.4). Если жидкость несжимаемая, то количество её между этими сечениями остаётся неизменным. Отсюда следует, что объёмы жидкости, протекающие в единицу времени через сечения 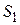 и
и 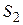 , должны быть одинаковыми:
, должны быть одинаковыми: 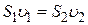 . Это равенство справедливо для любой пары произвольно взятых сечений. Следовательно, для несжимаемой жидкости при стационарном течении произведение
. Это равенство справедливо для любой пары произвольно взятых сечений. Следовательно, для несжимаемой жидкости при стационарном течении произведение 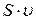 в любом сечении данной трубки тока имеет постоянное значение:
в любом сечении данной трубки тока имеет постоянное значение:

Это утверждение носит название теоремы о неразрывности струи. Она применима даже к газам, если их сжимаемостью можно пренебречь ( 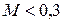 ). Примеры: 1) в узком месте река течёт быстро, в широком – медленно; 2) пожарный брандспойт имеет сужающийся наконечник, чтобы скорость воды была больше и струя летела дальше.
). Примеры: 1) в узком месте река течёт быстро, в широком – медленно; 2) пожарный брандспойт имеет сужающийся наконечник, чтобы скорость воды была больше и струя летела дальше.
Уравнение Бернулли
 Рассмотрим стационарное течение идеальной несжимаемой жидкости. Выделим трубку тока, а в ней объём жидкости, ограниченной стенками узкой трубки тока и перпендикулярными к линии тока сечениями
Рассмотрим стационарное течение идеальной несжимаемой жидкости. Выделим трубку тока, а в ней объём жидкости, ограниченной стенками узкой трубки тока и перпендикулярными к линии тока сечениями 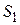 и
и 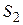 . За некоторое время
. За некоторое время 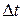 этот объём сместится вдоль трубки тока, причём граница объёма
этот объём сместится вдоль трубки тока, причём граница объёма 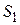 получит перемещение
получит перемещение 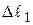 , а граница
, а граница 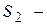 перемещение
перемещение 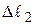 (рис. 5.5).
(рис. 5.5).
Работа, совершаемая при этом силами давления, равна приращению полной механической энергии: 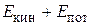 , заключённой в рассматриваемом объёме жидкости (на рис. 5.5 между сечениями 1 и 2).
, заключённой в рассматриваемом объёме жидкости (на рис. 5.5 между сечениями 1 и 2).
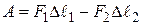
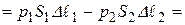
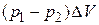 ,
,
где 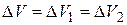 вследствие несжимаемости жидкости;
вследствие несжимаемости жидкости; 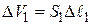 , а
, а 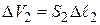 (на рисунке эти объёмы заштрихованы).
(на рисунке эти объёмы заштрихованы).
Полная энергия рассматриваемого объёма жидкости слагается из кинетической энергии и потенциальной энергии в поле сил земного тяготения. Возьмём сечения S трубки тока и перемещения 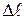 настолько малыми, чтобы всем точкам каждого из заштрихованных объёмов можно было приписать одни и те же значения скорости
настолько малыми, чтобы всем точкам каждого из заштрихованных объёмов можно было приписать одни и те же значения скорости 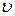 , давления
, давления 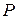 и высоты h. Приращение полной энергии (это разность полных энергий заштрихованных объёмов):
и высоты h. Приращение полной энергии (это разность полных энергий заштрихованных объёмов):
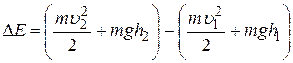 ,
,
так как 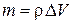 , то
, то
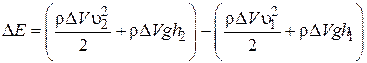 .
.
Приравняв А и DЕ, сократив на 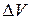 и перенеся члены с одинаковыми индексами в одну сторону, получим:
и перенеся члены с одинаковыми индексами в одну сторону, получим:

Заметим, что уравнение вполне строго лишь при 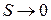 , т.е. для одной и той же линии тока. Так как
, т.е. для одной и той же линии тока. Так как 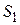 и
и 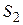 были выбраны произвольно, то можно утверждать, что для любой линии тока в стационарно текущей идеальной и несжимаемой жидкости выполняется условие (уравнение Бернулли):
были выбраны произвольно, то можно утверждать, что для любой линии тока в стационарно текущей идеальной и несжимаемой жидкости выполняется условие (уравнение Бернулли):

Уравнение выражает для движущейся жидкости закон сохранения механической энергии.
Для горизонтальной линии тока:

Если скорость течения вдоль линии тока возрастает, то давление падает, и наоборот. Уравнение используется, например, в аэродинамических измерениях скорости потока газа. Обычно измеряют полное давление 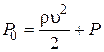 и статическое давление P в исследуемой точке потока, а значение скорости определяют как
и статическое давление P в исследуемой точке потока, а значение скорости определяют как 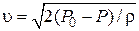 .
.
4. Течение вязкой жидкости. Формула Пуазейля. Для практических применений представляет особый интерес течение в круглой трубе (нефте- и газопроводы). Измерения показывают, что при медленном течении скорость частиц жидкости изменяется от нуля в непосредственной близости к стенкам трубы до максимума на оси трубы.
 Найдём закон изменения скорости по радиусу трубы. Выделим воображаемый цилиндрический объём жидкости радиусом r и длиной
Найдём закон изменения скорости по радиусу трубы. Выделим воображаемый цилиндрический объём жидкости радиусом r и длиной 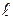 (рис. 5.6). При стационарном течении этот объём движется без ускорения. В направлении движения на жидкость действует сила давления, модуль которой равен
(рис. 5.6). При стационарном течении этот объём движется без ускорения. В направлении движения на жидкость действует сила давления, модуль которой равен 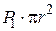 , во встречном направлении –
, во встречном направлении – 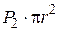 . Результирующая сила давления:
. Результирующая сила давления:
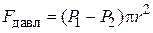 .
.
На боковую поверхность действует тормозящая сила трения:
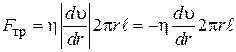 .
.
(Замечание: модуль отрицательного числа равен этому числу, взятому с обратным знаком).
Приравняв 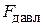 и
и 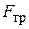 , получим:
, получим:
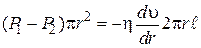 .
.
Производя сокращения и разделив переменные, получим:
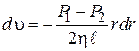 .
.
Интегрируем:
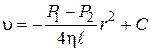 .
. 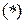
При 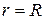
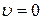 , отсюда
, отсюда
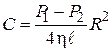 .
.
Подставим константу в выражение 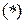 для
для 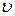 , получим:
, получим:
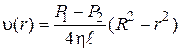 .
.
Скорость на оси трубы равна:
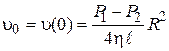 .
. 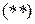
С учётом этого:

Вычислим поток жидкости Q, т.е. объём жидкости, протекающей через поперечное сечение трубы в единицу времени (рис. 5.7). Через кольцо радиусом 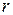 , шириной dr пройдёт в единицу времени объём жидкости dQ, равный произведению площади кольца
, шириной dr пройдёт в единицу времени объём жидкости dQ, равный произведению площади кольца 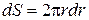 на скорость
на скорость 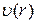 на расстоянии
на расстоянии 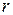 от оси трубы:
от оси трубы:
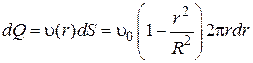 .
.
Проинтегрировав от 0 до R, получим:
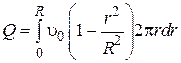
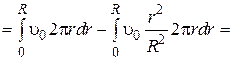
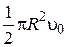 .
.
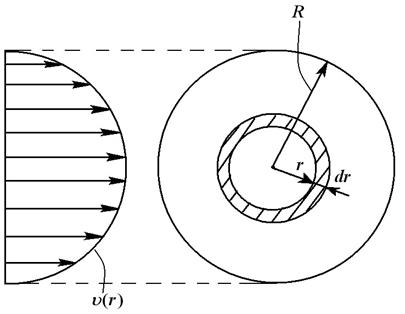
Рис. 5.7
Подставив значение 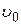 в выражение
в выражение 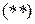 , получим формулу Пуазейля (французский учёный):
, получим формулу Пуазейля (французский учёный):

Физический смысл формулы: объём Q жидкости, протекающий за секунду через поперечное сечение трубы, прямо пропорционален разности давлений 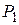 и
и 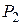 у входа в трубу и на выходе из неё, четвёртой степени радиуса трубы и обратно пропорционален длине
у входа в трубу и на выходе из неё, четвёртой степени радиуса трубы и обратно пропорционален длине 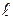 трубы и коэффициенту вязкости
трубы и коэффициенту вязкости 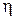 жидкости.
жидкости.
Формула справедлива только при ламинарном течении жидкости (см. далее). Формула применяется для определения коэффициента вязкости жидкостей, а также для оценки необходимого перепада давления для получения нужного объёмного расхода.
5. Ламинарный и турбулентный режимы течения. Если при течении жидкости слои жидкости скользят относительно друг друга не перемешиваясь, такое течение называется ламинарным (или слоистым; lamina – (лат.) пластина, плоская).
Ламинарное течение наблюдается обычно при медленном течении. Если увеличить скорость течения, то при достижении определенного значения скорости характер течения резко меняется. Скорость частиц в каждой точке пространства всё время быстро и нерегулярно изменяется. Такое течение называется турбулентным (turbulentus (лат.) – бурный, беспорядочный). При турбулентном течении происходит интенсивное перемешивание жидкости.
Английский физик Рейнольдс (1842 – 1912) установил, что характер течения определяется значением безразмерной величины:

где 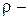 плотность жидкости (или газа);
плотность жидкости (или газа); 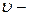 средняя по сечению трубы скорость потока;
средняя по сечению трубы скорость потока; 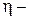 вязкость жидкости;
вязкость жидкости; 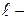 характерный для поперечного сечения потока размер, например диаметр при круглом сечении или сторона квадрата при квадратном сечении.
характерный для поперечного сечения потока размер, например диаметр при круглом сечении или сторона квадрата при квадратном сечении.
 Величина Re называется числом Рейнольдса. При малых Re течение носит ламинарный характер. Начиная с некоторого значения Re, называемого критическим, течение приобретает турбулентный характер. Значение Reкр для течения вязкой несжимаемой жидкости в круглой цилиндрической трубеоколо2,3×103. Примеры турбулентного течения: вода в горном потоке, за кормой корабля, дым из фабричной трубы и т.п.
Величина Re называется числом Рейнольдса. При малых Re течение носит ламинарный характер. Начиная с некоторого значения Re, называемого критическим, течение приобретает турбулентный характер. Значение Reкр для течения вязкой несжимаемой жидкости в круглой цилиндрической трубеоколо2,3×103. Примеры турбулентного течения: вода в горном потоке, за кормой корабля, дым из фабричной трубы и т.п.
6. Циркуляция скорости. Рассмотрим поле скоростей жидкости 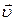 . В этом поле возьмём произвольный замкнутый контур L (рис. 5.8).
. В этом поле возьмём произвольный замкнутый контур L (рис. 5.8).
Пусть 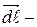 элемент длины контура. Интеграл
элемент длины контура. Интеграл 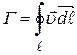 называется циркуляцией вектора скорости по контуру L. Если циркуляция скорости по любому замкнутому контуру, охватывающему обтекаемое тело, равна нулю, то движение жидкости (газа) называется потенциальным. В противном случае движение называется вихревым.
называется циркуляцией вектора скорости по контуру L. Если циркуляция скорости по любому замкнутому контуру, охватывающему обтекаемое тело, равна нулю, то движение жидкости (газа) называется потенциальным. В противном случае движение называется вихревым.
Н.Е. Жуковский (выдающийся русский механик, уроженец Владимирской губернии (1847 – 1921)) впервые установил вихревую природу сил, действующих со стороны потока на крыло, и указал на наличие простой зависимости между силой и циркуляцией скорости по контуру, охватывающему обтекаемое идеальной несжимаемой жидкостью крыло (рис. 5.9).
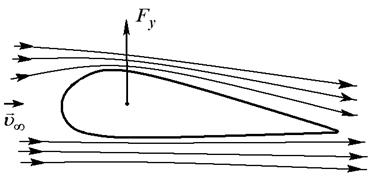
Рис. 5.9
Сверху профиль крыла выпуклый, линии тока сверху крыла сгущаются, сечение потока уменьшается, скорость больше, чем снизу, где профиль плоский. Циркуляция скорости потока по контуру профиля крыла оказывается отличной от нуля. Согласно формуле Жуковского возникает подъёмная сила на единицу длины крыла:

где 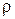 и
и 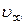 соответственно плотность потока и скорость невозмущённого крылом потока.
соответственно плотность потока и скорость невозмущённого крылом потока.
Вопросы для самоконтроля
1. Перечислите основные задачи механики жидкостей и газов.
2. В чём заключается понятие сжимаемости? Каким числом определяется сжимаемость?
3. Что такое вязкость? Какая жидкость называется идеальной?
4. Что называется линией тока, поверхностью тока, трубкой тока?
5. Запишите уравнение неразрывности. К каким средам оно применимо?
6. Запишите уравнение Бернулли. Какие законы (уравнения) использованы при его получении?
7. Запишите уравнение Бернулли для частных случаев:
а) жидкость неподвижна;
б) трубка тока расположена горизонтально.
8. Запишите формулу Пуазейля. Для какого режима течения она справедлива? Для каких целей может быть использована эта формула?
9. Что такое ламинарное и турбулентное течения? Сформулируйте условие перехода ламинарного режима течения в турбулентный.
10. Что выражает формула Жуковского?
Лекция № 6
Дата добавления: 2016-12-27; просмотров: 3346;











