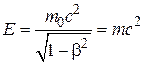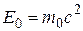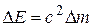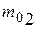ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

План

1. Принцип относительности Эйнштейна: постулат относительности, постулат постоянства скорости света. Роль скорости света. Преобразования Лоренца.

2. Лоренцево сокращение длины и замедление времени.

3. Релятивистский импульс. Взаимосвязь массы и энергии.

1. Принцип относительности Эйнштейна. Классическая механика, основанная на законах Ньютона, справедлива только для тел, движущихся со скоростями, много меньшими скорости света в пустоте ( 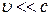). Для описания движений, совершающихся со скоростями, сравнимыми со скоростью света, Эйнштейн создал релятивистскую механику (relativus (лат.) – относительный). Различают специальную (являющуюся предметом нашего рассмотрения) и общую теорию относительности. Специальная означает рассмотрение явлений в инерциальных системах отсчёта.

В основе теории лежит принцип относительности, состоящий из двух постулатов:

1. Постулат относительности. Все законы природы и уравнения, их описывающие, инвариантны, т.е. не меняются при переходе от одной инерциальной системы отсчёта к другой (Замечание: неизменность вида уравнений при замене координат и времени одной системы отсчёта координатами и временем другой системы называется инвариантностью).

2. Постулат постоянства скорости света. Скорость света в вакууме не зависит от движения источника и приёмника света и одинакова во всех направлениях, т.е. скорость света в вакууме одинакова во всех инерциальных системах отсчёта.

Роль скорости света. Скорость света занимает особое положение в природе. В отличие от всех других скоростей, меняющихся при переходе от одной системы к другой, скорость света в пустоте является инвариантной величиной. Из постулатов Эйнштейна следует, что скорость света в вакууме является предельной: никакой сигнал, никакое воздействие одного тела на другое не могут распространяться со скоростью, превосходящей скорость света в вакууме. Именно предельный характер этой скорости и объясняет одинаковость скорости света во всех системах отсчёта. (Значение предельной скорости должно быть одинаково во всех инерциальных системах отсчёта).

Преобразования Лоренца (голландский физик, 1853 – 1928 гг.)

Рассмотрим две инерциальные системы отсчёта К и 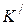. Пусть система 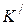движется относительно системы К со скоростью 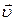(рис. 6.1).

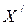Направим координатные оси так: Х и – совпадают и направлены параллельно вектору 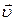, а ос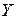и и 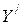– параллельны друг другу. Возьмём за начало отсчёта времени в обеих системах момент, когда начала координат О и 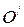совпадают ( 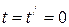). Предположим, что в момент времени t (в К-системе) в точке с координатами 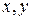(точка А) произошло некоторое событие, например вспыхнула лампочка.

Преобразования Лоренца дают связь координат 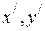и момента времени события 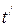в системе 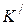с координатами 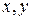и моментом времени t в системе К (прямые преобразования), и наоборот (обратные преобразования). Приводим их без вывода.

Прямые преобразования	Обратные преобразования

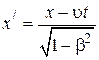
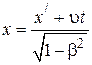
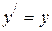
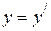
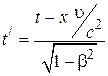
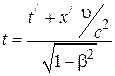
Здесь .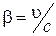

2. Лоренцево сокращение длины. Расположим неподвижный в системе 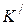стержень вдоль оси 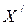. Пусть длина стержня в 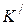-системе равна 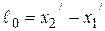(собственная длина стержня). В К-системе, относительно которой стержень движется, его длину определяют как расстояние 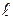между координатам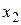и и 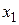его концов в один и тот же момент времени 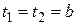. Воспользовавшись прямыми преобразованиями Лоренца, получим:

,

,

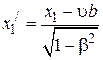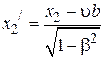вычитаем одно уравнение из другого:

,

,

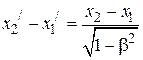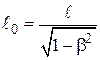или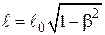

Так как 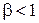, то .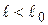

Таким образом, длина стержня, измеренная в системе, относительно которой он движется 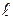, оказывается меньше длины 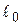, измеренной в системе, относительно которой стержень покоится. Это явление называется лоренцевым сокращением длины.

Замедление времени

Пусть в точке 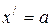, неподвижной относительно системы 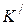, происходит событие, длящееся время 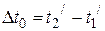. Относительно системы К начало и конец события (согласно обратным преобразованиям):

,

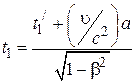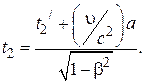
Вычитая из второго уравнения первое, получим:

.

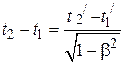Обозначим длительность события в системе К 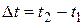, тогда

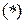
Так как 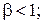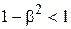, тогда .

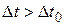Время 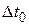, отсчитываемое по часам, движущимся вместе с телом, называется собственным временем тела. Таким образом, время, отсчитанное по часам, относительно которых система движется, всегда больше собственного времени (замедление времени).

Соотношение 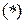получило непосредственное экспериментальное подтверждение. Среднее время жизни 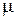-мезонов в условиях, когда они неподвижны (собственное время), порядка примерно 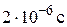. Образуются 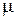-мезоны при взаимодействии космических лучей с атмосферой на высоте около 20 – 30 км.

Двигаясь со скоростью света (оценка «сверху»), 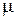-мезоны могут пройти путь лишь порядка 600 м. Однако они регистрируются и на Земле. Дело в том, что время, отсчитанное по часам экспериментатора, связанного с Землёй, оказывается гораздо большим ( 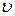близка к с), и пробег мезонов составляет около 30 км, и они достигают Земли.

В своё время недоверчивым скептикам Эйнштейн предлагал проделать мысленный эксперимент.

Пусть имеется движущийся вагон с лампочкой по середине. В некоторый момент лампочка вспыхивает.

Если наблюдатель находится в вагоне, то относительно него свет достигает задней и передней стенки вагона одновременно (рис. 6.2, а).

Если же наблюдатель находится вне вагона, то относительно него свет достигает задней стенки быстрее, чем передней (рис. 6.2, б). Мысленный эксперимент демонстрирует относительность понятия одновременности.

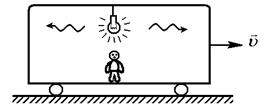
а)

б)

Рис. 6.2

3. Релятивистский импульс. Ньютоновское выражение импульса

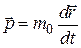. В релятивистской теории выражение для импульса, обеспечивающее инвариантность закона сохранения импульса и переход в ньютоновскую форму при 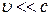, получается, если заменить время dt собственным временем частицы 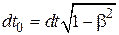, тогда

.

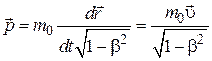В такой форме выражение

называется релятивистским импульсом. При 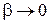релятивистское выражение переходит в ньютоновское 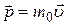. Постоянная величина 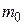называется массой покоя, поскольку является мерой инертности при нулевой скорости. Величина

называется релятивистской массой.

Взаимосвязь массы и энергии

Используя выражение для релятивистского импульса, запишем релятивистское уравнение движения:

(**)

Чтобы найти релятивистское выражение для энергии, умножим уравнение (**) на перемещение частицы :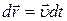

.

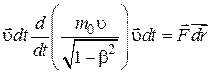Правая часть этого соотношения даёт работу 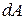, совершаемую над частицей за время dt. Из закона сохранения энергии следует, что работа, совершённая над частицей, должна быть равна приращению энергии частицы dE, т. е. .

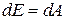Поэтому можно написать

.

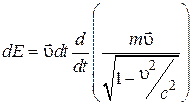Опуская дальнейшие преобразования, являющиеся весьма непростыми (некоторые любознательные читатели могут их найти в более полных курсах физики, например [2], [5]) приведём результат преобразований:

.

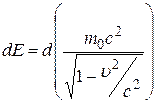Интегрирование полученного соотношения даёт:

 

 

Физический смысл этой формулы: полная энергия тела E (системы тел), из каких бы видов энергии она ни состояла (кинетической, электрической, химической и т.д.) связана с массой этого тела соотношением 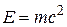. В полную энергию не входит потенциальная энергия тела во внешнем поле, если таковая действует на тело.

В том случае, когда тело покоится ( 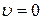), оно обладает энергией которая называется энергией покоя:

Из соотношения 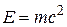вытекает, что энергия тела и его масса пропорциональны друг другу. Всякое изменение энергии тела 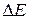(за исключением изменения потенциальной энергии во внешнем поле сил) сопровождается изменением массы тела, и наоборот.

Это утверждение называется законом взаимосвязи массы и энергии.

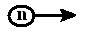
Пример. Рассмотрим реакцию деления ядер урана 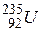при захвате медленных нейтронов:

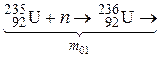
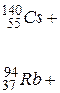
Суммарная масса покоя урана-235 и нейтрона превосходит суммарную массу покоя частиц в правой части ( 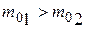) на 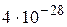кг. Отвечающая этому избытку массы энергия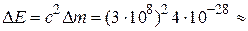 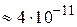Дж (на одну пару взаимодействующих частиц) превращается в кинетическую энергию образующих частиц и в энергию возникающего при делении электромагнитного излучения.

Создание атомных электростанций (как, впрочем, и создание атомной бомбы) стало возможным, в частности, благодаря теоретической основе – полученному Эйнштейном соотношению 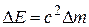. Это позволило нобелевскому лауреату Максу Борну заявить, что "идеи Эйнштейна дали физической науке импульс, который освободил её от устаревших философских доктрин и превратил в одну из решающих сил современного мира людей".

 

Вопросы для самоконтроля

1. При каких скоростях движения тел справедлива ньютоновская механика?

2. Сформулируйте принцип относительности Эйнштейна. Обратите внимание на общее и отличное в этом принципе и принципе относительности Галилея.

3. Сформулируйте постулат постоянства скорости света.

4. Получите из преобразований Лоренца выражение, описывающее длину тела в системе, относительно которой оно движется.

5. Получите из преобразований Лоренца формулу для определения промежутка времени между событием по часам, относительно которых система движется.

6. Запишите выражение для импульса в релятивистской форме.

7. Зависит ли масса от выбора системы отсчёта? Запишите выражение для массы в релятивистской физике.

8. Как связаны между собой полная энергия тела и релятивистская масса? Приведите примеры применения этой взаимосвязи.

 

 

<2345678>

---

Дата добавления: 2016-12-27; просмотров: 3794;

---