Теорема о движении центра инерции (масс)

Запишем 2-й закон Ньютона для 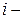й частицы массой .

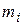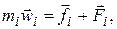
где 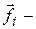внутренняя сила, действующая на 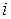-ю частицу (т.е равнодействующая сил, действующая со стороны других частиц системы на 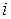-ю частицу); 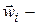ускорение 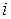-й частицы; 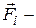внешняя сила, действующая на 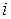-ю частицу.

Для всех тел (частиц) системы сумма

, (*)

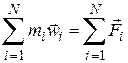так как 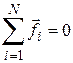по 3-му закону Ньютона (внутренние силы попарно равны по величине, направлены противоположно и действуют вдоль одной прямой).

Из определения центра масс следует:

.

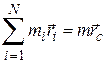Продифференцируем это выражение дважды:

,

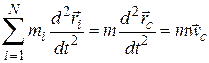где 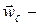ускорение центра масс.

. (**)

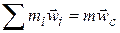Сравнив выражения(*) и (**), получим .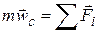

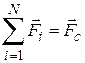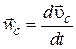Сумму внешних сил можно заменить равнодействующей , а (по определению), получим:

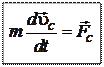
Центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы и сосредоточена в центре инерции (масс), а действующая сила – геометрической сумме всех внешних сил, действующих на систему (приложенных к точке С). Этот результат называется теоремой о движении центра масс (инерции).

Физический смысл этой теоремы заключается в том, что зачастую при движении тел (системы материальных точек) нас интересует не движение отдельных частей тела, а перемещение его в пространстве в целом. И в этом случае замена сложного (в общем случае) движения точек тела движением одной точки (центра масс) сильно упрощает задачу.

Вопросы для самоконтроля

1. Сформулируйте 1-й закон Ньютона. Что он устанавливает?

2. Сформулируйте 2-й закон Ньютона. Приведите пример использования этого закона как уравнения движения.

3. Сформулируйте 3-й закон Ньютона. Всегда ли он справедлив?

4. Когда возникает необходимость рассматривать силы инерции? Являются ли эти силы реальными?

5. Когда возникает центробежная сила инерции? Как ее рассчитывают?

6. При каких условиях возникает сила Кориолиса? Чему она равна?

7. Дайте определение центра инерции (центра масс).

8. Сформулируйте и докажите теорему о движении центра инерции (масс).

Лекция № 3