Второе начало термодинамики
Первое начало термодинамики не дает полной характеристики химических процессов, так как ничего не говорит об их направлении и возможности реализации.
Второе начало термодинамики решает вопрос о направлении естественных, самопроизвольно протекающих процессов и утверждает, что они приводят систему в более равновесное состояние. Существуют несколько различных формулировок второго начала термодинамики. Самым первым было определение, данное М.В. Ломоносовым:
«Холодное тело В, погруженное в тело А, не может воспринять большую степень теплоты, чем которую имеет тело А».
Другое определение (Сади Карно):
«Невозможен процесс, единственным результатом которого было бы превращение теплоты в работу».
Отсюда следует, что полностью превратить теплоту в полезную работу нельзя и что должны существовать границы и условия, при которых это превращение будет наибольшим.
Энтропия
Второе начало термодинамики тесно связанно с обратимостью процессов. В термодинамическом смысле обратимым называется процесс, который, можно провести не только в прямом, но и обратном направлении таким образом, что сама система и окружающая ее среда возвратятся в исходное состояние. Если в системе или окружающей среде остаются изменения, то такой процесс называется уже необратимым. Примером необратимых процессов, идущих самопроизвольно, притом только в одном направлении, являются:
Переход тепла от более нагретого тела к менее нагретому.
Химические реакции типа взрывных.
Взаимная диффузия газов или жидкостей и т. д.
Все эти процессы объединяет одно общее – участие в них тепловых явлений. Они самопроизвольно идут в одном направлении – выравнивание теплового состояния системы до термодинамического равновесия.
Вероятность существования различных состояний оценивает особая термодинамическая функция, называемая энтропией – S. Она растет с развитием необратимости процесса и достигает максимальных значений для данной системы при достижении последней термодинамического равновесия. В обратимых процессах энтропия остается постоянной. Наиболее вероятным состоянием системы будет такое, которому соответствует максимальное значение энтропии, а самопроизвольно развивающиеся процессы протекают по существу в одном направлении – возрастания величины энтропии. Энтропия является функцией состояния системы. Приращение энтропии dS выражается уравнением.
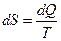
 [Дж/мольградус]
[Дж/мольградус]
Для каждого вещества в данном состоянии и при данной температуре существует одно определенное значение энтропии. В термодинамических таблицах значение энтропии приведено для стандартных условий; в этом случае вычисление энтропии S производят по уравнению
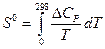

Если в интервале от 0 до 298 К вещество имеет агрегатные или аллотропические превращения, то учитывается и изменение энтропии в процессе эти превращений. Для вычислений принимают, что при абсолютном нуле в соответствии с третьим началом термодинамики величина энтропии любого вещества равна нулю. Значения энтропии для температур выше 298 К можно рассчитать с помощью уравнения
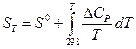

Дата добавления: 2016-12-09; просмотров: 1674;











