В процессе движения одна форма энергии может переходить в другую, однако полная удельная энергия идеальной жидкости остается без изменения по длине потока.
Уравнение Бернулли для потока вязкой жидкости
Поток реальной жидкости вследствие влияния вязкости отличается от элементарного потока идеальной жидкости неравномерностью распределения скоростей по течению и потерями энергии.
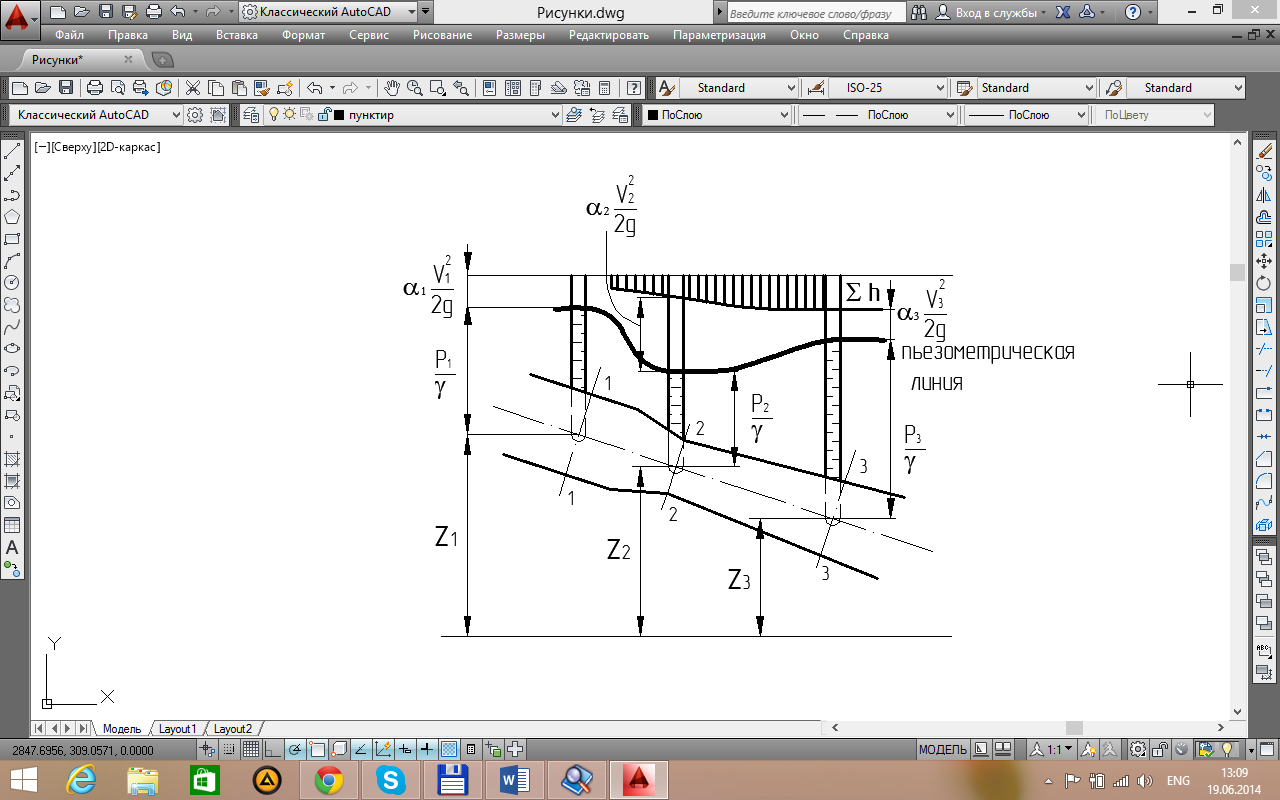
Рисунок 3.4
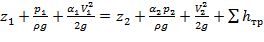 (3.9)
(3.9)
Гидростатический (потенциальный) напор для плавно изменяющегося движения (примерно, параллельноструйное) в пределах данного сечения есть величина постоянная для всех точек сечения, т.е.
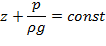
α – безразмерный коэффициент (коэффициент Кориолиса), учитывающий неравномерность распределения скорости и равный отношению кинетической энергии в сечении потока, вычисленным по действительным скоростям u, к кинетической энергии в том же сечении, вычисленной по средней скорости:
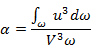
Сумма трех членов:
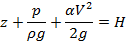
есть полный напор.
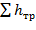 – потеря напора между выбранными сечениями потока.
– потеря напора между выбранными сечениями потока.
И выражение (3.6) можно написать:
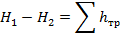
Графически это уравнение может быть представлено диаграммой подобной той, которую мы составляли для идеальной жидкости, но с учетом потери напора. Потеря напора представляет собой также некоторую высоту, которая неуклонно возрастает вдоль потока. Уравнение Бернулли для потока вязкой жидкости – это уравнение баланса энергии с учетом потерь.
Уменьшение среднего значения полной удельной энергии жидкости вдоль потока, отнесенное к единице длины называется гидравлическим уклоном:
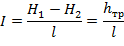
Изменение удельной потенциальной энергии жидкости, отнесенной к единице длины, называется пьезометрическим уклоном:
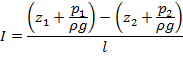
Дата добавления: 2016-06-15; просмотров: 2926;











