Идеальной жидкости (уравнения Эйлера).

В различных точках движущейся жидкости в результате действия внешних сил возникает давление, называемое гидродинамическим (в отличие от гидростатического, свойственного жидкости, находящейся в равновесии). Поэтому, как уже говорилось выше, одной из задач гидродинамики является определение величин гидродинамического давления, возникающего внутри жидкости, а также скоростей движения жидкости в различных точках пространства, занятого жидкостью. Для решения этих задач необходимо составить уравнения движения жидкости, связывающие между собой скорости и ускорения с силами, действующими на жидкость.

Рассмотрим движение элементарного жидкого тела. Введем обозначения: p- гидродинамическое давление, u- скорость движения жидкости в точке с координатами x, y, z; u_x, u_y, u_z- составляющие скорости по осям координат. Предположим, что на движущуюся жидкость действуют объемные силы, проекции которых на оси координат, отнесенные к единице массы (иначе, проекции ускорений), равны X, Y, Z.

Общие уравнения движения идеальной жидкости могут быть получены из дифференциальных уравнений равновесия той же жидкости, если согласно принципу д’Аламбера, к действующим силам присоединить силы инерции. Проекции сил инерции, которые должны быть присоединены к уравнениям равновесия, также отнесем к единице массы, т.е. в виде:

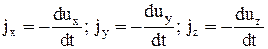
Знак (-) показывает, что силы инерции направлены в сторону, противоположную ускорению.

Присоединив к дифференциальным уравнениям Эйлера (2-8) проекции сил инерции, получим:

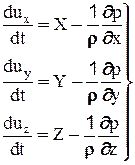(2-27)

Полученная система уравнений (2-27) устанавливает связь между объемными силами и скоростями, давлением и плотностью жидкости и называется уравнениями Эйлера. Смысл каждого из уравнений заключается в следующем: полное ускорение частиц вдоль координатной оси складывается от ускорения массовых сил и ускорения от сил давления.