Уравнение Бернулли для струйки идеальной жидкости.

Воспользуемся дифференциальными уравнениями движения (2-27). Умножим первое уравнение на dx, второе - на dy, третье - на dz:

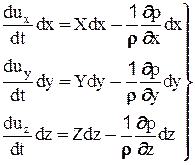(2-28)

Cложим систему уравнений:

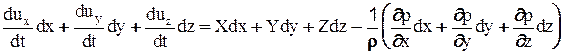(2-29).

Будем рассматривать струйку, которая при установившемся движении является траекторией движения частиц. В этом случае dx, dy, dz будут проекциями элементарного пути dL, проходимого частицами за время dt, т.е. dx=u_xdt, dy=u_ydt, dz=u_zdt. Подставим эти значения в левую часть уравнения (2-29), учитывая, что полная скорость u выражается через составляющие по осям координат :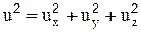

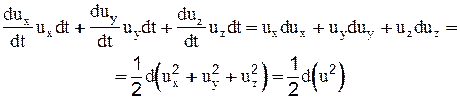
В правой части уравнения (2-29) выражение Xdx+Ydy+Zdz=dU - является полным дифференциалом силовой функции U (см. уравн. 2-9).

Т.к. мы рассматриваем установившееся движение, при котором гидродинамическое давление не зависит от времени, то трехчлен в скобках уравнения (2-29) представляет собой полный дифференциал давления:

.

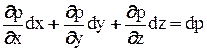Итак, уравнение (2-29) можно привести к виду:

,

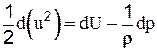или

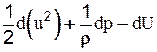(2-30)

Уравнение (2-30) устанавливает связь между скоростью u, давлением p и силовой функцией U для любого сечения струйки движущейся жидкости.

Проинтегрировав уравнение (2-30), получим

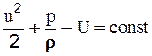(2-31)

Т.е. для двух любых сечений элементарной струйки можем записать:

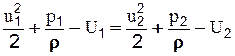(2-32)

Рассмотрим частный случай, когда из внешних объемных (массовых) сил на жидкость действует только сила тяжести. Тогда, силовая функция, соответствующая силе тяжести, может быть представлена, таким образом:

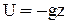
Подставляя значение U в уравнение (2-32), получим

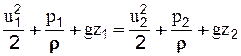(2-33)

Ранее отмечалось, что все слагаемые отнесены к единице массы. Отнесем слагаемые уравнения (2-33) к единице веса жидкости, помня, что вес единицы массы равен g. Разделив левую и правую части уравнения на g, получим:

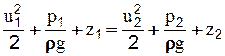(2-34)

Зависимость (2-34) является уравнением Бернулли для элементарной струйки идеальной жидкости, оно устанавливает связь между скоростью движения u, давлением p и геометрическим положением сечений струйки z. Впервые получено Даниилом Бернулли в 1738 г. в результате применения к движущейся жидкости закона сохранения энергии. Это уравнение дало возможность решать многие практические задачи гидравлики.