Идеальной жидкости (уравнения Эйлера)

Выделим в жидкости элементарный параллелепипед с ребрами dx,dy,dz. Рассмотрим равновесие действующих на этот параллелепипед внешних сил. Составим уравнения проекций этих сил на координатные оси. Ограничимся подробным рассмотрением уравнения проекций на ось X.

Рис.2.4.

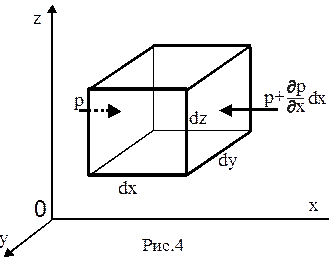
Давление зависит от координат(см. свойства гидростатического давления), поэтому на параллельных гранях (рис.2.4.) параллелепипеда оно различно. При переходе от одной грани к другой параллельной изменилась только одна координата x (на величину dx), и давление изменилось от значения p до p+ 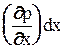, где 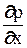- частный дифференциал, взятый по координате X. Таким образом, на левую грань действует сила 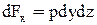, а на правую 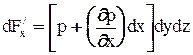. Найдем проекцию массовых сил dG на ось X - это произведение элементарной массы dm=rdxdydz на проекцию ускорения X этих сил на ту же ось, т.е. dG_x =rdxdydzX. Просуммировав и приравняв к нулю проекции всех сил получим первое уравнение равновесия:

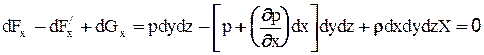
Разделив на rdxdydz (т.е. отнесли к единице массы), получим:

.

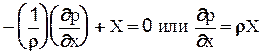Аналогичные уравнения получим для проекций на оси Y и Z.

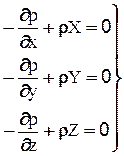(2-8)

Это и есть дифференциальные уравнения равновесия идеальной жидкости. Впервые выведены в 1775г. Л. Эйлером и выражают в дифференциальной форме закон распределения давления.

Для дальнейшего исследования преобразуем систему дифференциальных уравнений (2-8). Умножив каждое из уравнений соответственно на dx, dy,dz, и сложив систему уравнений получим:

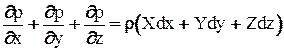
Т.к. гидростатическое давление является функцией только координат точки 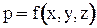, то левая часть уравнения представляет собой полный дифференциал давления dp. Следовательно dp=r(Xdx+Ydy+Zdz). Т.к. r=const, то последнее уравнение может иметь смысл только в том случае, если выражение в скобках также является полным дифференциалом. Для этого необходимо, чтобы существовала такая функция U=f(x,y,z), частные производные которой по x, y, z были бы соответственно равны 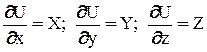Такая функция называется потенциальной, а силы, которые этой функцией выражаются, - силами, имеющими потенциал (например, силы тяжести):

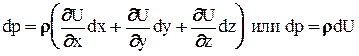(2-9)