Методы моделирования

Моделированием называется метод изучения реального или создаваемого объекта (оригинала), при котором вместо него используется модель, а результаты распространяются на оригинал. Суть моделирования заключается в предсказании поведения оригинала в рабочих условиях производства по измеренным параметрам модели. Методы моделирования основаны на подобии различных объектов.

Подобными называются явления, для которых постоянны отношения характеризующих их исходных величин. Условия подобия рассмотрим на простейшем примере геометрического подобия. Подобные фигуры отличаются друг от друга только масштабом и могут быть получены одна из другой умножением сходственных размеров одной из них на некоторый постоянный масштабный множитель (константу подобия).

Например, если размеры сторон одного треугольника равныа¢, в¢ ис¢, а размеры сходственных сторон подобного ему треугольника составляют а², в², с², то:

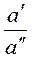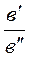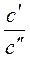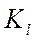= = = = const . (1-7)

Однако, соблюдение геометрического подобия аппаратов является условием необходимым, но не достаточным. При подобии физических процессов должны быть подобны все основные физические величины, влияющие на него. Поэтому технологические процессы подобны только при соблюдении так называемых условий однозначности, т.е. совместного обеспечения геометрического и временного подобия, подобия полей физических величин, а также начальных и граничных условий.

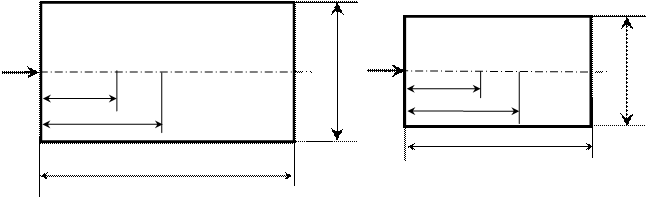
Сформулируем эти условия на примере подобного движения вязкой жидкости в производственном трубопроводе (оригинале) и в его уменьшенной модели (рис. 2.1).

Рис. 1.1. Подобие физических процессов

Для этого рассмотрим любые сходственные точки, лежащие, например, на оси труб: А¢₀ и А²₀ и т.д.

Геометрическое подобие соблюдается при равенстве отношений всех сходственных линейных размеров оригинала и модели:

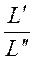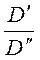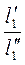= = = … = const = 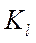. (1-8)

При подобном движении сходственных частиц их траектории в оригинале и в модели также должны быть подобны. Это условие называют кинематическим подобием.

Временное подобиехарактеризуется тем, что сходственные частицы в геометрически подобных системах, двигаясь по геометрически подобным траекториям, проходят подобные пути за промежутки времени, отношение которых является постоянной величиной, т.е.

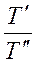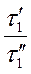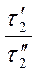= = = … = const = 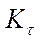, (1-9)

Т¢, Т² - время прохождения сходственными частицами трубопровода и его модели.

При соблюдении геометрического и временного подобия будет соблюдаться также подобие скоростей

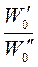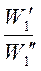= = … = const = К_w . (1-10)

Подобие физических величинпредполагает, для двух любых сходственных точек оригинала и модели, размещенных подобно в пространстве и времени, отношения физических свойств являются величинами постоянными. Так, например,

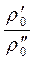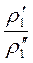= = … = const = К_r ,

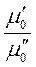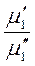= = … = const = К_m и т.д. (1-11)

Подобие начальных и граничных условийпредполагает, отношения основных параметров в начале и на границе оригинала и модели являются соответственно величинами постоянными.

Подобие потоков в оригинале и модели можно охарактеризовать также с помощью инвариантов подобия, т.е. в виде отношений сходственных величин в пределах каждой системы.

Так:

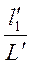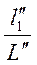= = idem = 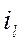, (1-12)

idem - означает инвариантно или "одно и тоже".

Величина 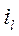- представляет собой инвариант подобия геометрических величин.

Инварианты подобия, выраженные отношением двух однородных физических величин с одинаковыми разностями, называются симплексами. Однако инварианты подобия могут быть выражены также отношениями разнородных величин, т.е. представлять собой их безразмерные комплексы._ Например, для сходственных точек подобных потоков в трубопроводе и его модели равны инварианты подобия, состоящие из различных физических величин:

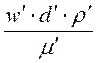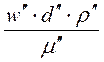= =idem = Re(критерий Рейнольдса). (1-13)

Безразмерные комплексы, составленные по такому типу, называются критериями подобия. Последние всегда имеют физический смысл, являясь мерами соотношения между какими-то двумя эффектами (силами и т.п.), существенными для рассматриваемого процесса. Критерии подобия обладают всеми свойствами инвариантов: они безразмерны, могут изменять свою величину от точки к точке данной системы и т.д.

Критерии подобия могут быть получены для любого процесса, если известны аналитические зависимости между характеризующими его величинами - дифференциальные уравнения, описывающие процесс.

Однако дифференциальные уравнения описывают целый класс однородных по своей сущности явлений и для выделения из него конкретного явления необходимо ограничивать указанные уравнения дополнительными условиями (условиями однозначности). Они включают: геометрическую форму и размеры системы, существенные для данного процесса физические константы участвующих в нем веществ, начальные и граничные условия, временное подобие. Таким образом, дифференциальные уравнения должны решаться в совокупности с условиями однозначности в устанавливаемых последними пределах.

Основные положения теории подобия обобщаются тремя теоремами подобия. Они лежат в основе практического применения теории подобия.

Теоремы подобия

Первая теорема подобиябыла сформулирована Ньютоном. "Подобные явления характеризуются численно равными критериями подобия" или при подобии систем всегда могут быть найдены такие безразмерные комплексы величин, которые для сходственных точек данных систем одинаковы. В качестве примера возьмем второй закон Ньютона.

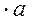f = m = m 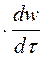. (1-14)

Выделим в двух подобных системах (натуре и модели) две частицы, движущиеся подобно. Пусть в оригинале на частицу массой m¢ действует силаf¢, сообщая ей ускорение 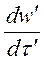; в модели соответственно m²; f²; 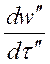.Тогда:

f¢ = m¢¢ 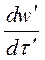и f² = m² .

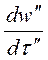При подобном движении, при условии, что отношение приращений величин, можно заменить отношениями самих величин

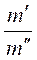= К_m; 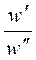= К_w ; 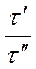= К_t и, как следствие,

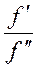= К_f, или К_f = 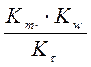, откуда С = 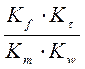= 1.

Величину С, составленную из констант подобия, называют индикатором подобия.

Перепишем так;

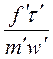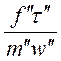= . (1-15)

Безразмерный комплекс величин, значения которого одинаковы для сходственных точек, называют критерием Ньютона:

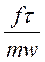= idem = Ne или 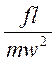= Ne t= l /w.

Критерий Ньютона характеризует отношение действующей на частицу силы к силе инерции.

Первая теорема подобия указывает, какие величины следует измерять при проведении опытов, результаты которых требуется обобщить: надо измерять те величины, которые входят в критерии подобия.

Вторая теорема подобия. Решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде зависимости между безразмерными комплексами этих величин, т.е. между критериями подобия.

Критерии подобия, которые составлены только из величин, входящих в условия однозначности, называются определяющими, а остальные определяемыми. Из критериального уравнения, представляющего собой функциональную зависимость между критериями подобия, рассчитав предварительно значения определяющих критериев, находят величину определяемого. А из него - численное значение интересующей нас величины. Тогда, если определяемым является критерий p₁, то

p₁ = f(p₂ , p₃ ,…, p_n ) (1-16)

Вторая теорема подобия отвечает на вопрос, как обрабатывать результаты опытов, проведенных на моделях: их надо представлять в виде функциональной зависимости между критериями подобия.

Третья теорема подобияили теорема М.В. Кирпичева и А.А. Гухмана, формулирует необходимые и достаточные условия подобия явлений: подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и у которых соблюдается подобие условий однозначности. Для этого необходимо равенство определяющих критериев подобия. Тогда третья теорема может быть сформулирована так: явления подобны, если их определяющие критерии численно равны.

Следствием равенства определяющих критериев, согласно выражению (2-10), является равенство определяемых критериев для модели и оригинала.

Таким образом, исследование процессов методом теории подобия должно состоять из следующих этапов:

1. Получив полное математическое описание процесса, т.е. составив дифференциальное уравнение и установив условия однозначности, проводят подобное преобразование этого уравнения и находят критерии подобия.

2. Опытным путем на моделях устанавливают конкретный вид зависимости между критериями подобия. Причем полученная зависимость справедлива для всех подобных явлений в исследованных пределах изменения определяющих критериев подобия.

Контрольные вопросы

1. Каким общим законом описываются процессы пищевой технологии? Как его можно записать?

2. Содержание и последовательность расчетов аппаратов пищевых производств.

3. Какими показателями характеризуются периодический и непрерывный процессы? Их преимущества и недостатки.

4. Как рассчитываются объемы аппаратов периодического и непрерывного действия?

5. Чем обуславливается необходимость использования метода моделирования при исследовании и расчете аппаратов?

6. Как получают критерии подобия? Какие критерии гидродинамического подобия Вы знаете?

7. Что такое условия однозначности?