Жидкость. Основные физические свойства

Жидкостью называется физическое тело, обладающее большой подвижностью частиц, которая объясняется слабой связью между молекулами. Жидкость не имеет своей формы, но принимает форму сосуда, в котором она находится. Жидкость легко деформируется, не дробясь на части, под действием небольших сил и поэтому обладает текучестью. Все жидкости делятся на капельные и газообразные. Капельная жидкость имеет объем, и если объем меньше объема сосуда, то жидкость занимает часть объема сосуда и образует свободную поверхность. В отличие от капельных жидкостей газы, как упругие жидкости, не имеют своих определенной формы и объема. Они всегда занимают весь объем сосуда, в котором находятся.

В гидравлике изучаются законы равновесия и движения только капельных жидкостей, которые обладают свойством текучести и очень мало изменяют плотность при изменении давления, т.е. практически несжимаемы.

Плотностью (r) называют количество массы (m) жидкости, содержащееся в единице ее объема (V):

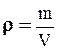; кг/м³ (2-1)

Удельным(или объемным) весом жидкости (g)называют вес (G ) единицы ее объема (V):

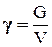; Н/м³ (2-2)

Из выражений (2-1) и (2-2) можно получить связь между плотностью и удельным весом. Т.к. G=mg, то получим: g=rg

Удельный объем - это объем жидкости V, занимаемый единицей массы m: 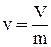; м³/кг. Удельный объем есть величина, обратная плотности:

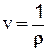; м³/кг.

Сжимаемость - это свойство жидкости изменять свой объем при изменении давления. Характеризуется коэффициентом объемного сжатия b_v:

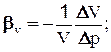м²/Н (2-3)

где: V- начальный объем, м³

DV - изменение объема, м³

Dp - изменение давления, Па

Величина обратная b_v называется модулем объемной упругости: K=1/b_v

Капельные жидкости характеризуется очень малой сжимаемостью, поэтому в гидравлике сжимаемостью обычно пренебрегают, за исключением отдельных случаев.

Температурное расширение - изменение объема жидкости в зависимости от температуры. Характеризуется температурным коэффициентом объемного расширения b_t.:

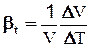⁰К^-1 (⁰С^-1) (2-4)

где DT - изменение температуры.

Рис.2.1.

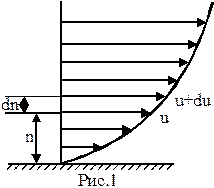
Вязкость - свойство реальных жидкостей оказывать сопротивление сдвигающим касательным усилиям. Это свойство обнаруживается лишь при движении жидкости. Жидкость движется (течет) вдоль плоской стенки (неподвижной). Вследствие тормозящего влияния стенки слои жидкости будут двигаться с разными скоростями, значения которых возрастают по мере отдаления от стенки. Рассмотрим слои со скоростями u и u+du , отстоящих друг от друга на расстоянии dn. Приращение скорости на единицу длины по нормали к направлению оси потока называют градиентом скорости 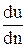. Экспериментально показано, что касательная сила T, которую надо приложить к верхнему слою для его равномерного сдвига относительно нижнего слоя, тем больше, чем больше градиент скорости 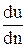. Сила T пропорциональна площади соприкосновения слоев S, т.е.:

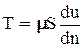(2-5)

где m - коэффициент пропорциональности, зависящий от рода жидкости и ее температуры и называется динамический коэффициент вязкости. В СИ размерность Па с.

Отношение T/S=t есть касательное напряжение (или напряжение внутреннего трения, или напряжение сдвига.). Тогда 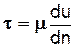. Величину t можно считать всегда положительной, поэтому в зависимости от знака 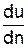формулу (5) следует представить в виде:

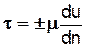(2-6)

Знак зависит от закона, изменения скорости по нормали к потоку и выбора направления нормали. Уравнение (2-6) выражает закон внутреннего трения Ньютона.

Внутреннее трение характеризуется также кинематической вязкостью:

n=m/r; м²/с

Рис.2.2.

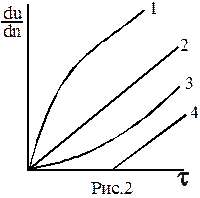
Существуют жидкости для которых зависимость (2-6) неприменима. Жидкости, которые не подчиняются закону внутреннего трения Ньютона называются неньютоновскими или аномальными. Для ньютоновских жидкостей кривые течения (или реограммы), т.е. кривые, изображающие зависимость между градиентом скорости течения жидкости 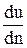и возникающим в ней касательным напряжением t, носят линейный характер (рис.2.2.). Для неньютоновских жидкостей кривые течения весьма многообразны и в общем случае не являются линейными. Расположение этих кривых на графике и их форма определяют класс неньютоновских жидкостей и характеризуют особенности ее течения. Кривая 1 на рис. 2.2. - дилатантные жидкости. Кривая2 - обычная ньютоновская жидкость. Кривая 3 - псевдопластичные жидкости. Кривая 4 -вязкопластичные жидкости.

В общих курсах гидравлики обычно изучают лишь ньютоновские жидкости, неньютоновские, как правило, здесь не рассматриваются, этим занимается реология.