ТЕМПЕРАТУРНОЕ ПОЛЕ.ТЕПЛОВОЙ ПОТОК
Температурное состояние тела или системы тел можно охарак-теризовать с помощью температурного поля, под которым понимается совокупность значений температур во всех точках рассматриваемого пространства (тела) в данный момент времени. Математически темпе-ратурное поле может быть описано уравнением зависимости температур Т от трех пространственных координат х, y, z и от времени t. Поэтому в общем случае
Т= f(x,y,z ,t). (2.1)
Так как температура – скаляр, то и температурное поле скалярно.
Температурное поле, которое изменяется во времени, называется нестационарным (неустановившемся). Такому полю отвечает неста-ционарный (неустановившийся) тепловой режим. В стационарном (установившемся) температурном поле температуры разных точек тела могут быть разными, но не изменяющимися во времени. В этом случае тепловой режим будет также стационарными. Уравнение стационарного температурного поля
Т= f(x,y,z). (2.2)
Во многих случаях может рассматриваться зависимость температурного поля не только от трех, но и от двух, а иногда и от одной координаты. В соответствии с этим различают одномерные, двухмерные и трехмерные температурные поля. На практике довольно часто встречаются задачи, когда температура тела является функцией одной координаты. Например, одномерной является задача о переносе теплоты в стенке, у которой длину и ширину можно считать бесконечно большими по сравнению с толщиной.
Графически температурное поле изображают посредством изотерми-ческих поверхностей, под которыми понимается геометрическое место точек с одинаковой температурой. Такие поверхности могут быть замкнуты или выходить за границы тела. Форма и положение такой поверхности в пространстве меняются во времени, если поле нестационарное, и остаются неизменными, если поле стационарное. Кривые, образующиеся в результате пересечения изотермической поверхности и плоскости, называютсяизотермами(рис. 2.1). Поскольку в одной и той же точке не может быть одновременно двух значений температуры, изотермические поверхности, так же как и изотермы, никогда не пересекаются – они либо заканчиваются на поверхности тела, либо замыкаются сами на себя.
 |
 Т4
Т4


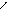





Т2
 Т3
Т3
Рис. 2.1. Изотермы
По расположению изотерм можно оценить интенсивность изменения температуры в различных направлениях: чем чаще расположены изо-термы, тем интенсивнее изменяется температура. Наибольший перепад температуры на единицу длины происходит по нормали к изотерми-ческой поверхности (рис. 2.2).
Предел отношения изменения температуры ΔТ к расстоянию между изотермами по нормали Δn, когда Δn стремится к нулю, называютградиентом температуры
gradТ= n0 ·∂Т/ ∂n =i· ·∂Т/ ∂x +j· ∂Т/ ∂y + k· ∂Т/ ∂z, (2.3)
где n0 - единичный вектор нормали к изотермической поверхности;
i, j, k – орты системы координат.
Таким образом, градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону увеличения темпе-ратуры и численно равный частной производной от температуры по этому направлению. За положительное направление градиента прини-
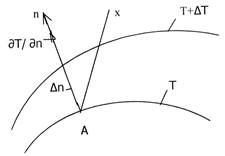 |
мается направление возрастания температур.
Рис. 2.2. Расположение вектора градиента температуры
Количество теплоты, переносимой за единицу времени через произвольную изотермическую поверхность площадью F, называется тепловым потоком Q, единицей измерения которого служит ватт(вт).
Конечной целью большинства теплотехнических расчетов, связанных с оценкой теплопереноса, является определение количества теплоты, которое передается или воспринимается 1 м2 поверхности каждого из участвующих в теплообмене тел в единицу времени. Эта величина называется плотностью теплового потока q; единицей измерения q является ватт на квадратный метр (вт/м2). Связь между Q и q устанав-ливается из определений:
q = dQ/dF, Q =∫q dF. (2.4)
F
Если q остается неизменным по поверхности F, то
Q = q F. (2.5)
ЗАКОН ФУРЬЕ.
Дата добавления: 2021-02-19; просмотров: 809;











