Формулы исчисления высказываний. Таблицы истинности
Формулы исчисления высказываний –это высказывания, которые могут быть получены из элементарных высказываний (например A, B, 1, 0) посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции. Формулы необходимы для исчисления истинности или ложности составных высказываний, то есть решения логических задач.
Особое значение в логике исчисления высказываний имеют тождественные высказывания и эквивалентные высказывания (формулы де Моргана). Если высказывания в таблице истинности характеризуются либо одними единицами, либо только нулями, то это означает, что они, либо всегда истинны, либо ложны, независимо от истинности входящих в них высказываний. Например, высказывание 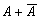 всегда истинно, а высказывание
всегда истинно, а высказывание 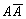 всегда ложно. Сложные высказывания, истинные при любых значениях входящих в них других высказываний, называются тождественно истинными, а высказывания, ложные при любых значениях входящих в них других высказываний, называются тождественно ложными. Правила де Моргана имеют вид:
всегда ложно. Сложные высказывания, истинные при любых значениях входящих в них других высказываний, называются тождественно истинными, а высказывания, ложные при любых значениях входящих в них других высказываний, называются тождественно ложными. Правила де Моргана имеют вид:
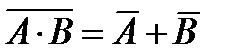 ;
;
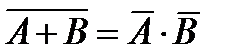 .
.
Полезными также являются следующие законы:
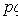
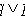
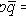
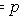 (закон склеивания),
(закон склеивания),
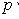
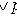
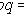
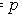 (закон поглощения),
(закон поглощения),
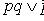

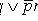
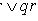 (закон обобщенного склеивания).
(закон обобщенного склеивания).
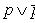
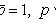
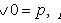
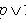
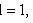
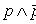
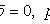
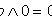
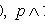
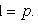
Тождественно истинные или тождественно ложные высказывания, если они встречаются в формулах, заменяются в них, соответственно единицей или нулем:
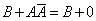 ,
, 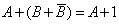 .
.
Среди высказываний встречаются также и такие, в которых таблицы истинности совпадают. Эти высказывания называются эквивалентными. Эквивалентными являются, например, высказывания 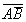 и
и 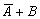 .
.
Дата добавления: 2016-05-31; просмотров: 1986;











