Операции с плавающей точкой

Правило сложения (вычитания):

пусть, 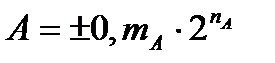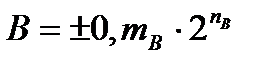– два нормализованных двоичных числа, и 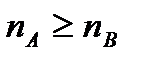(в противном случае мы можем просто поменять их местами). В результате их сложения или вычитания будет получено следующее выражение:

.

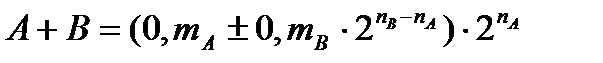Последовательность вычислений следующая:

1. Порядки чисел A и B выравниваются по большему из них (в нашем случае это n_A). Для этого мантисса числа B сдвигается на n_A-n_B разрядов вправо (часть значащих цифр при этом могут оказаться утерянными), а его порядок становится равным n_A.

2. Выполняется операция сложения (вычитания) над мантиссами с округлением по значению n+1-ой значащей цифры результата.

3. Мантисса результата должна быть нормализована (получившийся после нормализации порядок может отличаться от n_A как в меньшую, так и в большую сторону).

Если порядки равны, сложение-вычитание выполняется следующим образом:

Тогда:

Если порядки отличаются, то необходимо вначале их выровнять:

После чего нужно привести m₂p^n2-n1 к нормальному (т.е. к обычному, без показателя степени) виду, сложить с m₁, полученный результат и будет мантиссой суммы, а порядком суммы будет n1.

Умножение-деление

Тогда:

То есть, при умножении нужно перемножить мантиссы и сложить показатели степени, при делении – разделить мантиссы и вычесть из показателя степени делимого показатель степени делителя. Например:

Основные понятия алгебры высказываний. Логические операции