Системы счисления. Операции над числами в различных системах счисления

Кроме десятичной существует неизмеримое количество других систем, при этом некоторые из них используются для представления и обработки информации в компьютере. Существуют два вида систем счисления: позиционные и непозиционные.

Непозиционными системами называются такие, у которых каждая цифра сохраняет свое значение независимо от места нахождения в числе. Примером может служить римская система счисления, в которой используются такие цифры как I, V, X, L, C, D, M и т.д.

Позиционными называются системы счисления, в которых значение каждой цифры зависит от её места положения. Позиционная система характеризуется основой исчисления, под которой будет пониматься такое число £, которое показывает, сколько единиц какого-либо разряда необходимо для получения единица старшего порядка.

Например, можно записать

.

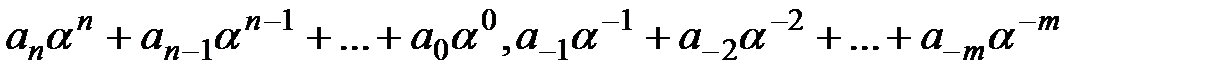Что соответствует числам в десятичной системе счисления

,

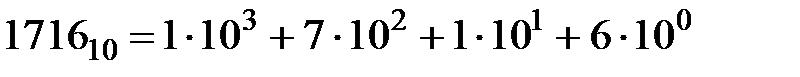
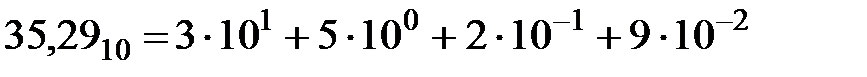Индекс снизу указывает на основу счисления.

Для перевода положительных чисел, из одной системы счисления в другую известны два правила:

- перевод чисел из системы 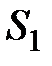, в систему 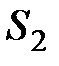с использованием арифметики системы ;

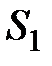- перевод чисел из системы 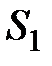, в систему 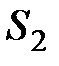с использованием арифметики системы ;

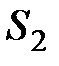Рассмотрим первое правило. Допустим, число в десятичной системе 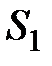необходимо представить в двоичной системе 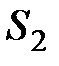. Для этого данное число делится на основание системы 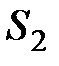представленное в системе 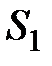, т.е. на 2₁₀. Остаток от деления будет младшим разрядом двоичного числа. Целая часть результата от деления вновь делится на 2. Операцию деления повторять столько раз, пока частное не будет меньше двух.

Пример: 89₁₀ перевести в двоичное число, пользуясь арифметикой десятичной системы счисления

89₁₀ → 1011001₂

Обратный перевод, согласно того же правила, следующий:

1011001₂ перевести в десятичное число, пользуясь арифметикой двоичной системы счисления

Двоичные числа 1000 и 1001 согласно таблице 2.1 соответственно равны 8 и 9. Поэтому 1011001₂ → 89₁₀

Иногда обратный перевод удобнее осуществлять, пользуясь общим правилом представления числа в какой-либо системе исчисления.

Рассмотрим второе правило. Перевод чисел из системы 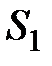, в систему 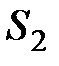с использованием арифметики системы 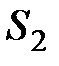. Для осуществления перевода необходимо каждую цифру числа в системе 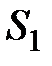умножить на основание системы счисления 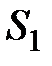представленной в системе счисления 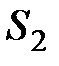и в степени позиции этого числа. После чего полученные произведения суммируются.